oporu ośrodka wyrażona prawem Stokesa F = 6Rv (skierowana pionowo w górę)
ciężaru ciała
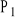
=
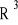
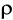
g (skierowana pionowo w dół)wyporu
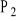
=
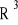
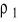
g (skierowana pionowo w górę)
Wyznaczanie współczynnika lepkości metodą Stokesa. |
|||
Ćwiczenie wykonali |
Konrad Lubaski Kamil Matysek |
||
Wydział |
Grupa |
Zespół |
Data |
Budownictwo |
II |
1 |
23.10.2002 |
Rok akademicki |
Semestr |
Ocena |
Podpis |
2002/2003 |
I |
|
|
Teoretyczne omówienie doświadczenia
Do przeprowadzenia doświadczenia potrzebny będzie cylinder z badaną cieczą, a także kulki (ołowiane lub szklane). Na kulkę o promieniu R spadającą swobodnie w cieczy o współczynniku lepkości h będą działać trzy siły:
oporu ośrodka wyrażona prawem Stokesa F = 6Rv (skierowana pionowo w górę)
ciężaru ciała ![]()
= ![]()
![]()
![]()
g (skierowana pionowo w dół)
wyporu ![]()
= ![]()
![]()
![]()
g (skierowana pionowo w górę)
![]()
- gęstość kulki, ![]()
- gęstość cieczy
Na początku kulka ma ruch przyspieszony. Ze wzrostem prędkości kulki, siła oporu rośnie i przyspieszony ruch kulki przechodzi w ruch jednostajny. Wtedy gdy kulka ma ruch jednostajny, wszystkie siły muszą się równoważyć więc mamy równanie:
F + ![]()
= ![]()
F = ![]()
- ![]()
6Rv = ![]()
![]()
![]()
g - ![]()
![]()
![]()
g
6Rv = ![]()
![]()
g(![]()
-![]()
)
![]()
![]()
![]()
g
Ponieważ prędkość kulki jest stała, to mierząc czas opadania kulki t na odcinku drogi h można użyć wzoru v = ![]()
i podstawić go:
![]()
![]()
![]()
gt
Wyrażenie to jest słuszne dla naczyń bardzo szerokich. Jeżeli kulka opada w rurze cylindra, której promień równy ![]()
porównywalny jest z promieniem kulki R, to wówczas wyrażenie przyjmie postać:
![]()
![]()
![]()
gt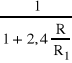
Gliceryna
Gęstość kulki |
11342 [kg * m-3] |
Średnica kulki |
0,00255 [m] |
Gęstość gliceryny |
1260 [kg * m-3] |
Przyspieszenie ziemskie |
9,71 [m * s-2] |
Średnica cylindra |
0,026 [m] |
Odległość A-B |
0,4 [m] |
Numer pomiaru |
R1 [m] |
R [m] |
h [m] |
t [s] |
|
s*m-2 |
1 |
0,026 |
0,00250 |
0,4 |
2,30 |
0,813 |
0,7818 |
2 |
0,026 |
0,00247 |
0,4 |
2,70 |
0,814 |
0,8959 |
3 |
0,026 |
0,00258 |
0,4 |
2,38 |
0,807 |
0,8616 |
4 |
0,026 |
0,00262 |
0,4 |
2,32 |
0,805 |
0,8661 |
5 |
0,026 |
0,00253 |
0,4 |
2,44 |
0,811 |
0,8494 |
6 |
0,026 |
0,00250 |
0,4 |
2,24 |
0,813 |
0,7614 |
7 |
0,026 |
0,00262 |
0,4 |
2,34 |
0,805 |
0,8735 |
8 |
0,026 |
0,00249 |
0,4 |
2,44 |
0,813 |
0,8227 |
9 |
0,026 |
0,00262 |
0,4 |
2,40 |
0,805 |
0,8959 |
10 |
0,026 |
0,00259 |
0,4 |
2,38 |
0,807 |
0,8683 |
Wartość średnia |
0,026 |
0,00255 |
0,4 |
2,39 |
0,809 |
0,8452 |
Dyskusja błędu
Niepewność systematyczna związana z włączeniem i wyłączeniem stopera.
![]()
Niepewność systematyczna związana z dokładnością stopera.
![]()
Niepewność przypadkowa - wartość średniego odchylenia poszczególnych czasów opadania kulek od wartości średniej.
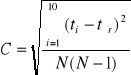
![]()
Niepewność całkowita związana z czasem.
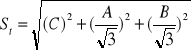
![]()
Niepewność systematyczna związana z odczytem średnicy kulki.
![]()
Niepewność systematyczna związana z dokładnością śruby mikrometrycznej.
![]()
Niepewność przypadkowa - wartość średniego odchylenia poszczególnych średnic kulek od wartości średniej.
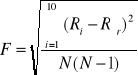
![]()
Niepewność całkowita związana ze średnicą kulek.
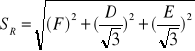
![]()
Niepewność systematyczna związana z dokładnością mierzenia średnicy cylindra.
![]()
Niepewność systematyczna związana z dokładnością mierzenia wysokości.
![]()
Niepewność całkowita
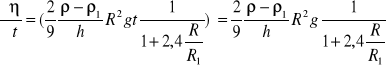
![]()
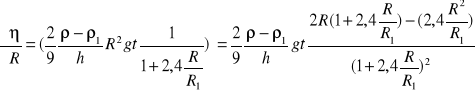
![]()
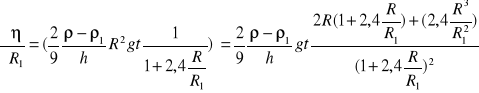
![]()
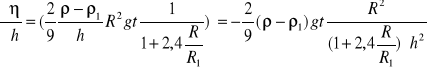
![]()
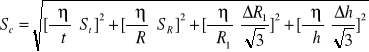
![]()
Olej silikonowy
Gęstość kulki |
11342 [kg * m-3] |
Średnica kulki |
0,00257 [m] |
Gęstość oleju silikonowego |
976 [kg * m-3] |
Przyspieszenie ziemskie |
9,71 [m * s-2] |
Średnica cylindra |
0,026 [m] |
Odległość A-B |
0,4 [m] |
Numer pomiaru |
R1 [m] |
R [m] |
h [m] |
t [s] |
|
s*m-2 |
1 |
0,026 |
0,00260 |
0,4 |
2,95 |
0,806 |
1,1151 |
2 |
0,026 |
0,00258 |
0,4 |
3,01 |
0,807 |
1,1203 |
3 |
0,026 |
0,00259 |
0,4 |
3,13 |
0,807 |
1,1740 |
4 |
0,026 |
0,00263 |
0,4 |
3,11 |
0,805 |
1,2029 |
5 |
0,026 |
0,00264 |
0,4 |
3,03 |
0,804 |
1,1808 |
6 |
0,026 |
0,00250 |
0,4 |
2,79 |
0,813 |
0,9750 |
7 |
0,026 |
0,00248 |
0,4 |
3,00 |
0,814 |
1,0317 |
8 |
0,026 |
0,00265 |
0,4 |
3,03 |
0,803 |
1,1898 |
9 |
0,026 |
0,00254 |
0,4 |
2,71 |
0,810 |
0,9776 |
10 |
0,026 |
0,00257 |
0,4 |
2,95 |
0,808 |
1,0895 |
Wartość średnia |
0,026 |
0,00257 |
0,4 |
2,97 |
0,808 |
1,0969 |
Dyskusja błędu
Niepewność systematyczna związana z włączeniem i wyłączeniem stopera.
![]()
Niepewność systematyczna związana z dokładnością stopera.
![]()
Niepewność przypadkowa - wartość średniego odchylenia poszczególnych czasów opadania kulek od wartości średniej.
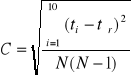
![]()
Niepewność całkowita związana z czasem.
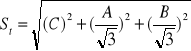
![]()
Niepewność systematyczna związana z odczytem średnicy kulki.
![]()
Niepewność systematyczna związana z dokładnością śruby mikrometrycznej.
![]()
Niepewność przypadkowa - wartość średniego odchylenia poszczególnych średnic kulek od wartości średniej.
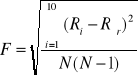
![]()
Niepewność całkowita związana ze średnicą kulek.
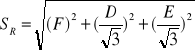
![]()
Niepewność systematyczna związana z dokładnością mierzenia średnicy cylindra.
![]()
Niepewność systematyczna związana z dokładnością mierzenia wysokości.
![]()
Niepewność całkowita
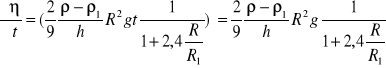
![]()
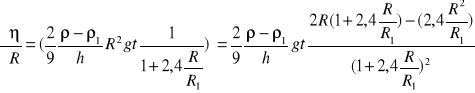
![]()
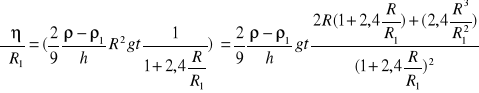
![]()
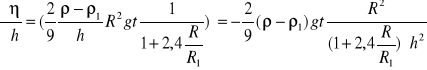
![]()
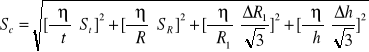
![]()
- 1 -