Wyznaczenie bezwzględnego współczynnika lepkości metodą Stokesa.

Pomiar współczynnika lepkości za pomocą wiskozymetru Ostwalda.

Wykonali:

xxx

xxx

Grupa 2a

Zespół 1

Kierunek: Inżynieria Środowiska

Wydział: Ochrony Środowiska i Rybactwa

Zjawisko lepkości

Zjawiskami zachodzącymi podczas przepływu i spoczynku płynów zajmuje się mechanika płynów i reologia. Pod pojęciem płynu należy rozumieć ciało, którego cząsteczki odznaczają się tak znaczną ruchliwością, że powolną zmianę geometrycznej postaci można wywołać znikomo małymi siłami. Ciała te nie wykazują zatem sprężystości postaci - przyjmują kształt naczynia, w którym sięznajdują. Płyny dzielą się na ciecze i gazy. Stanem równowagi cieczy zajmuje się hydrostatyka, a ruchem cieczy hydrodynamika.

Ciecz doskonała

Ciecz doskonałą cechuje brak lepkości, ściśliwości, rozszerzalności cieplnej i napięć powierzchniowych. Ciecz doskonała ma stałą gęstość, niezależną od temperatury i ciśnienia.

Ruch laminarny

Uwarstwiony ruch płynu, w którym można wyodrębnić przesuwające się względem siebie warstwy cieczy.
Każda warstwa w ruchu laminarnym płynu porusza się z prędkością różniącą się od prędkości sąsiedniej warstwy o dowolnie małą różnicę prędkości
. Zakładamy, że warstwy te są odległe o dowolnie mały odcinek
. Wzdłuż przekroju poprzecznego strumienia płynu, płynącego w przewodzie zachodzi więc spadek prędkości o wartości:

Mierząc w kierunku od środka strugi do ścianek przewodu. Wyrażenie to pozwala obliczyć wartość gradientu prędkości w kierunku prostopadłym do przepływu płynu.

Równanie opisujące właściwości lepkie płynów, zapisane w postaci wzoru na siłę oporu lepkiego
lub naprężnie styczne
, nazywa się często równaniem Newtona. Ciecze spełniające równanie Newtona, czyli takie, dla których współczynnik lepkości nie zależy od prędkości ruchu cieczy, są to tzw. ciecze niutonowskie.

Współczynnik lepkości dynamicznej
, jak każdy współczynnik proporcjonalności, wprowadzony do zapisu matematycznego zależności między wielkościami fizycznymi, zależy od rodzaju substancji, a dla danego płynu - od temperatury i ciśnienia. Dynamika płynów posługuje się również pojęciem lepkości kinematycznej. Współczynnik lepkości kinematycznej jest to stosunek współczynnika lepkości dynamicznej do gęstości płynu

Jest to więc współczynnik lepkości przedstawiony w odniesieniu do jednostki masy. Współczynnik lepkości można wyznaczyć ze wzoru Newtona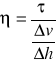

Współczynnik lepkości dynamicznej liczbowo równa się ciśnieniu statycznemu, które powstaje przy ruchu względnym dwóch warstw cieczy, jeżeli spadek prędkości tych warstw równa się jedności.

Zgodnie z równaniem Newtona jednostką współczynnika lepkości dynamicznej w układzie SI jest jeden paskal razy sekunda.

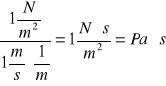
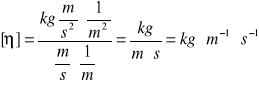
Wymiar współczynnika lepkości kinematycznej to:

Współczynnik lepkości jest ważnym parametrem reologicznym charakteryzującym właściwości lepkie i lepkosprężyste ciał. Wartości współczynników lepkości poszczególnych płynów znacznie różnią się miedzy sobą.
Współczynniki lepkości zarówno dynamicznej, jak i kinematycznej dla cieczy maleją wraz ze wzrostem temperatury, natomiast praktycznie nie zależą od ciśnienia w granicach umiarkowanych ciśnień i dopiero przy bardzo dużych ciśnieniach ich wartości rosną.
Współczynniki lepkości gazów rosną wraz ze wzrostem temperatury i ciśnienia.

Względną lepkość kinematyczną określamy wzorem:

W technice i praktyce rolniczej często wyrażamy lepkość względną w stopniach Englera, np. lepkość mleka, smarów i olejów. Istnieje wiele metod pomiaru lepkości dostosowanych do konkretnych potrzeb i warunków pracy laboratoryjnej.

Wyznaczanie bezwzględnego współczynnika lepkości metodą Stokesa

Na ciało poruszające się w cieczy działają siły oporu lepkiego hamujące ruch ciała. Jeżeli np. kulka spada w cieczy, to warstwa cieczy bezpośrednio przylegająca do kulki porusza się z prędkością równą prędkości kulki, pociągają za sobą następne warstwy cieczy. Mamy więc do czynienia z przesuwaniem się warstw cieczy względem siebie. Między warstwami cieczy działa siła lepkości, czyli na kulkę poruszającą się w cieczy działa siła oporu lepkiego. Związek między siłą oporu lepkiego a prędkością kulki, jej promieniem i właściwościami cieczy znalazł Stokes i wyraził wzorem:

Gdzie:

F - siła oporu lepkiego

- współczynnik lepkości dynamicznej cieczy
r - promień kulki
v - prędkość kulki

Wzór ten jest słuszny dla ruchu laminarnego, tzn., gdy ruch kulki nie powoduje powstawania wirów, czyli warstwy cieczy przesuwają się równolegle względem siebie.

Do pomiaru lepkości cieczy służy rura szklana ustawiona pionowo. Do rury wlewamy badaną ciecz i wpuszczamy kulkę o małym promieniu w porównaniu z promieniem rury (w celu uniknięcia wirów).

Na kulkę o objętości
działają trzy siły:
1. Siła przyciągania ziemskiego, która działa pionowo w dół:

2. Siła oporu lepkiego działająca pionowo w górę:

3. Siła wyporu skierowana pionowo w górę:

W pierwszym momencie kulka w cieczy porusza się ruchem przyspieszonym, ponieważ siła P jest większa niż siła F + W. Po przebyciu pewnej drogi, wskutek wzrostu prędkości siła F wzrośnie do takiej wartości, że wraz z siłą W zrównoważy siłę P, zatem ruch kulki stanie się jednostajny. Mamy wtedy:

Wiemy, że siła ciężkości

- gęstość kulki

- objętość kulki
r - promień kulki
g - przyspieszenie ziemskie

Siła wyporu:

- gęstość cieczy

Bezwzględny współczynnik lepkości:

Pomiar współczynnika lepkości za pomocą wiskozymetru Ostwalda

Do pomiaru współczynnika lepkości w laboratoriach technologicznych i w laboratoriach medycznych używa się często prostego w konstrukcji wiskozymetru kapilarnego. Wiskozymetr Ostwalda jest jednym z typów wiskozymetrów kapilarnych, w których bada się przepływ cieczy przez przewody kapilarne.
Zjawiskiem tym rządzi prawo Poiseuille'a, które wyraża się wzorem:

Gdzie:

- objętość cieczy wypływającej w ciągu 1 s (natężenie przeływu)

- współczynnik bezwzględnej lepkości dynamicznej cieczy

- promień kapilary

- długość kapilary

- różnica ciśnień na końcach rurki

W praktyce okazało się, że posługując się wzorem Poiseulle'a dogodniej jest wyznaczyć lepkość względną. Zasada pomiaru jest następująca: badamy czas przepływu tej samej objętości cieczy badanej i wody destylowanej przez tę samą kapilarę ustawioną pionowo. Możemy wówczas napisać:

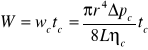
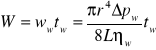
Gdzie:

- czas wypływu cieczy badanej o objętości W

- czas wypływu wody destylowanej o objętości W

- różnica ciśnień na końcach kapilary napełnionej cieczą

- różnica ciśnień na końcach kapilary napełnionej wodą destylowaną

Po podzieleniu równań stronami otrzymujemy:

Przepływ cieczy przez kapilarę wywołują siły ciężkości, dlatego różnica ciśnień hydrostatycznych na końcach kapilary jest proporcjonalna do gęstości cieczy, a więc:

Podstawiając tę wartość do równania
, otrzymujemy wzór na względny współczynnik lepkości dynamicznej:

Gdzie:

- gęstość cieczy badanej

- gęstość wody destylowanej

---