Sprawozdanie z ćwiczenia nr 65

WYZNACZANIE PROMIENIA KRZYWIZNY SOCZEWKI ZA POMOCĄ PIERŚCIENI NEWTONA

1

ZAGADNIENIA TEORETYCZNE

Interferencja światła
Interferencją fal nazywamy zjawisko nakładania się fal, w których zachodzi stabilne w czasie ich wzajemne wzmocnienie w jednych punktach przestrzeni, oraz osłabienie w innych, w zależności od stosunków fazowych fal. Interferować mogą tylko fale spójne, dla których odpowiadające im drgania zachodzą wzdłuż tego samego lub podobnych kierunków.
Jeżeli założymy, że dwa punktowe źródła emitują dwie fale sinusoidalne o amplitudach A₁ i  A₂, częstościach kołowych ₁ i ₂ i fazach ₁(t) i _( to wypadkowa fala będzie opisana równaniem
.(1)

Jeżeli fale są niespójne, to

i natężenie fali wypadkowej jest równe sumie natężeń fal składowych. Podczas nakładania się fal spójnych amplituda fali wypadkowej zmienia się od A=A₁-A₂ do A=A₁+A₂ w zależności od wartości trzeciego członu w równaniu (1). W najprostszym przypadku, aby zaszła interferencja muszą być spełnione następujące warunki

₁=₂ oraz ₁(t)-₂(t)=const.

    Podczas nakładania się światła pochodzącego z dwóch źródeł nie będących laserami lub nawet pochodzących z różnych miejsc tego samego źródła nie obserwujemy interferencji. Jest to spowodowane przez emisję światła przez wzbudzone atomy w postaci skończonych ciągów falowych, których fazy początkowe zmieniają się niezależnie. Dwie fale nazywamy falami spójnymi jeżeli różnica ich faz nie zależy od czasu. Spójne fale świetlne ze zwykłych (nielaserowych) źródeł otrzymujemy metodą dzielenia światła pochodzącego z jednego źródła na dwie lub więcej wiązek. Promieniowanie w każdej z nich pochodzi od tych samych atomów źródła i ze względu na wspólne pochodzenie, wiązki te są spójne. Do podziału światła na wiązki spójne można wykorzystać zjawiska odbicia lub załamania światła.
Okazuje się jednak, że powyższe warunki są zbyt silne i interferencję możemy obserwować nawet wtedy, gdy częstości nakładających się fal nie są dokładnie równe. Również nie musimy używać źródeł o punktowych rozmiarach. W ogólności, interferujące ze sobą fale muszą mieć spełnione tzw. Interferencję fal świetlnych najlepiej ilustruje doświadczenie Younga, przedstawione na rysunku poniżej. Silnym źródłem światła oświetlamy, poprzez czerwony filtr, szczelinę o szerokości około 0,2 - 0,3 mm. W tak otrzymanej wiązce światła umieszczamy układ dwu szczelin. Odległość szczelin nie powinna być większa niż 0,2 - 0,3 mm. Szczeliny te służą do wytworzenia dwu identycznych fal (fal spójnych). Efekt interferencji (nakładania się) fal obserwujemy za pomocą lupy lub okularu mikroskopu (15x).

Interferencja światła jest wynikiem dodawania dwóch promieni świetlnych. Energia elektryczna promienia świetlnego rośnie i maleje na przemian, podobnie jak energia potencjalna w ruchu falowym. Jeśli drgania w dwóch falach są zgodne mówimy, że fale są w fazie. Promienie świetlne są w fazie, gdy w każdym punkcie ich energia elektryczna jednocześnie rośnie albo maleje. Następuje wtedy dodawanie energii i w rezultacie powstaje jeden, jasny promień. O takiej interferencji mówimy, że jest konstruktywna. Jeśli jednak promienie spotykają się w taki sposób, że energia elektryczna jednego z nich rośnie, a drugiego maleje, czyli są w przeciwfazie, wtedy odejmują się wzajemnie. Wynikiem tego odejmowania jest brak światła, czyli ciemne miejsce. Taką interferencję nazywamy destruktywną.

Interferencja zachodzi dla wszystkich rodzajów fal. W przypadku światła interferencja powoduje powstawanie na przemian jasnych i ciemnych pasm. Skutkiem tego zjawiska są kolory baniek mydlanych. Białe światło odbija się zewnętrznej i wewnętrznej powierzchni bańki. Powstają dwa rozszczepione promienie, które interferują ze sobą tak, że niektóre kolory stają się jaśniejsze, inne przygaszone, zależnie od miejsca. Jeżeli rozpatrzymy najprostszy przypadek interferencji fal pochodzących z dwóch źródeł o długości λ, które leżą od punktu P w odległościach d₁ i d₂ opisanych zależnością: y(P₁) = sin(t + φ₁) + sin(t + φ₂), gdzie:

to okaże się, że φ₁ − φ₂ = kλ fala ulega podwójnemu wzmocnieniu, a w przypadku gdy:

fale się wygaszają. Wartość φ, nazywana fazą fali zmienia się wraz z odległością od źródła. Gdy w jednym miejscu spotkają się fale o przeciwnej fazie, to nastąpi ich wygaszenie. Pierścienie Newtona - zjawisko optyczne polegające na nierównomiernym załamywaniu się światła, przechodzącego poprzez bardzo cienkie warstwy powietrza (ale nie tylko) o nierównej grubości, zawartego pomiędzy dwoma innymi materiałami przezroczystymi o innym współczynniku załamania światła. Widoczne jest jako prążki interferencyjne w postaci tęczowych pasm o nierównomiernych kształtach.Występowanie pierścieni Newtona jest szczególnie dokuczliwe w DTP podczas skanowania materiałów transparentnych, gdyż w wynikowych plikach graficznych obraz tych prążków jest szczególnie trudny do usunięcia. W celu uniknięcia tego zjawiska stosuje się skanowanie materiałów transparentnych przyklejonych specjalnymi środkami bezpośrednio do płyty lub cylindra skanera, wprowadza się olej w miejsce szpary powietrznej, umieszcza w specjalnych kopertach, z których następnie powietrze jest odsysane, lub też umieszcza w specjalnych ramkach zapewniających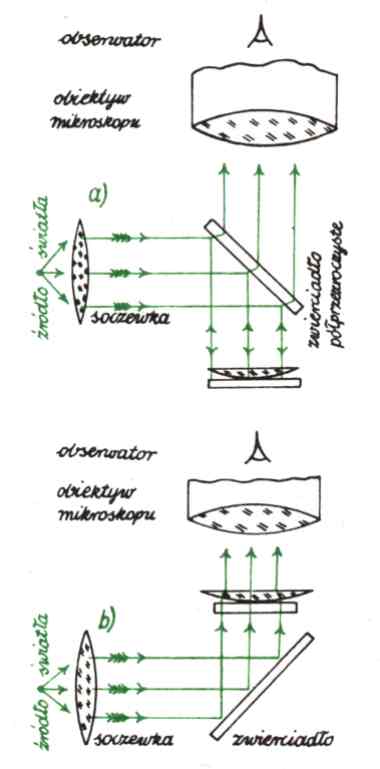
sąsiednich elementów skanera.

Powstaje ono, gdy mamy do czynienia z odbiciem światła od górnej i dolnej powierzchni cieniutkiej warstewki powietrza a zmiennej grubości między płaską płytką szklaną a soczewką szklaną (rys. 1).

Rys. 1. Układ do obserwacji pierścieni Newtona: a - "z góry", tzn. w świetle odbitym; b - "z dołu", tzn. w świetle przechodzącym.

Obserwator widzi wtedy barwne koła (rys. 2).

Rys. 2. Pierścienie Newtona obserwowane w świetle odbitym przy użyciu światła: a - czerwonego, b - niebieskiego.

Opis doświadczenia:

Podłączyłam lampę sodową do kontaktu. Zgasiłam światło i obserwowałam pod mikroskopem pojawianie się na soczewce okręgów. Ustawiłam wskazówki na środku i dla ośmiu krążków wykonałam dwukrotnych pomiarów średnic. Uzyskane wyniki zanotowałam.

Opracowanie wyników pomiarów:

Obliczam średnie arytmetyczne uzyskane z pomiarów [mm]:

OX w lewo ; OX w prawo ; OY w dół ; OY w górę

Prążek ósmy: 24,47±0,01 ; 33,21±0,01 ; 18,46±0,01 ; 9,77±0,01

Prążek dziesiąty: 23,94±0,01 ; 33,76±0,01 ; 19,01±0,01 ; 9,22±0,01

Prążek dwunasty: 23,45±0,01 ; 34,22±0,01 ; 19,45±0,01 ; 8,76±0,01

Prążek czternasty: 23,00±0,01 ; 34,62±0,01 ; 19,92±0,01 ; 8,30±0,01

Prążek piętnasty: 22,87±0,01 ; 34,82±0,01 ; 20,12±0,01 ; 8,90±0,01

Prążek szesnasty: 22,60±0,01 ; 35,03±0,01 ; 20,31±0,01 ; 7,89±0,01

Prążek siedemnasty: 22,40±0,01 ; 35,22±0,01 ; 20,50±0,01 ; 7,70±0,01

Prążek osiemnasty: 22,06±0,01 ; 35,60±0,01 ; 20,90±0,01 ; 7,33±0,01

Obliczam wartości długości promieni prążków:

8:

10:

12:

14:

15:

16:

17:

18:

Wyznaczam promienie krzywizny soczewki dla kolejnych obliczonych wartości promieni pierścieni:

k=8 :

k=10:

k=12:

k=14:

k=15:

k=16:

k=17:

k=18:

Obliczam średnią arytmetyczną promienia krzywizny soczewki:

R_ŚR=[4,03+4,50+4,06+4,09+3,79+4,09+4,09+4,34]m : 8 = 4,12m

Obliczam złożoną niepewność standardową:

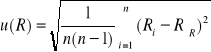
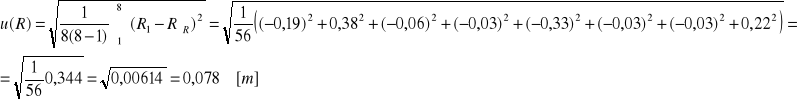
Wnioski:

Za pomocą pierścieni Newtona można wyznaczyć krzywiznę badanej soczewki. Na podstawie doświadczenia i obliczeń można stwierdzić, iż promień naszej soczewki miał długość 4,12m± 0,078m, czyli zawiera się w przedziale [4,198m ; 4,042m]. Wynik podany jest z niepewnością (0,078:4,12)=1,9%, czyli jest bardzo dokładny.

Na błąd podczas pomiarów pierścieni Newtona wpłynęły między innymi:

1. słaba dokładność wyznaczenia położenia środka pierścieni

2. błąd paralaksy podczas odczytu pokrywania się krzyża okularu ze styczną danego okręgu, szybkie zmęczenie oka

3. nieduże powiększenie mikroskopu.

Mimo powyższych trudności udało się uzyskać dokładny wynik. Oznacza to, że zjawisko nierównomiernego załamania światła wykorzystane w tym doświadczeniu jest , wraz z przyrządem Newtona, dobrym układem do badania i obserwacji właściwości fal świetlnych.

---