1. HIPOTEZA STATYSTYCZNA. DEFINICJA, PRZYKŁADY METODY WERYFIKACJI.

Hipoteza statystyczna - każde przypuszczenie dotyczące rozkładu lub charakterystyk rozkład określonej zmiennej losowej, o prawdziwości lub fałszywości którego wnioskuje się na podstawie pobranej próbki.

Rodzaje hipotez statystycznych:

1. parametryczna - hipoteza, która dotyczy wyłącznie wartości parametru określonej klasy rozkładów

2. nieparametryczna - każda hipoteza, która nie jest parametryczna

3. prosta - jeżeli hipoteza parametryczna precyzuje dokładne wartości wszystkich nieznanych parametrów rozkładu badanej cechy

4. złożona - hipoteza, która nie jest prostą

2. TEST STATYSTYCZNY. POJĘCIE, ZASTOSOWANIE, RODZAJE

Test statystyczny - reguła postępowania, za pomocą której, na podstawie wyników próby losowej, decydujemy o przyjęciu lub odrzuceniu sprawdzanej hipotezy

Rodzaje testów statystycznych:

1. testy parametryczne - służą do weryfikacji hipotez parametrycznych

2. testy nieparametryczne - służą do weryfikacji hipotez nieparametrycznych

1. testy niezależności - służą do weryfikacji skojarzeń cech

2. testy zgodności - mają na celu ustalenie typu rozkładu rozważanej zmiennej losowej

3. testy istotności - pozwalają na odrzucenie hipotezy sprawdzanej z małym ryzykiem popełnienia błędu I rodzaju lub stwierdzenia, że brak jest podstaw do jej odrzucenia.

3. WERYFIKACJA HIPOTEZ STATYSTYCZNYCH. RODZAJE POPEŁNIANYCH BŁĘDÓW. METODY MINIMALIZACJI PRAWDOPODOBIEŃSTWA POPEŁNIENIA BŁĘDU.

Sprawdzając hipotezę statystyczną, można popełnić dwojakiego rodzaju błędy. Odrzucenie hipotezy zerowej gdy jest ona prawdziwa, nosi nazwę błędu pierwszego rodzaju, a przyjęcie hipotezy zerowej gdy jest ona fałszywa - błędu drugiego rodzaju. Prawdopodobieństwo popełnienia błędu pierwszego rodzaju jest oznaczone przez α, zaś prawdopodobieństwo popełnienia błędu drugiego rodzaju oznacza się przez β.

Udowodniono, że przy danej próbie n-elementowej zmniejszenie prawdopodobieństwa α popełnienia błędu I rodzaju powoduje wzrost prawdopodobieństwa β popełnienia błędu II rodzaju i odwrotnie. Aby rozwiązać ten problem, można najpierw zmniejszać α, aby następnie - przez zwiększenie liczebności próby n - obniżyć również prawdopodobieństwo β do wymaganego poziomu i w ten sposób zwiększyć moc testu.

4. SCHEMAT POSTEPOWANIA PRZY WERYFIKACJI HIPOTEZ STATYSTYCZNYCH PRZY POMOCY TESTÓW ISTOTNOŚCI

W testach istotności nie oblicza się błędu drugiego rodzaju. Przy założeniu prawdziwości weryfikowanej hipotezy budujemy zbiór krytyczny w ten sposób, aby zagwarantować małe prawdopodobieństwo zaobserwowania wartości statystyki testowej należącej do tego zbioru, równe z góry obranemu poziomowi istotności α. Jeżeli zatem wartość statystyki testowej wpadnie do wyznaczonego uprzednio obszaru krytycznego, to można twierdzić, że zaszło zdarzenie o małym prawdopodobieństwie i wówczas weryfikowaną hipotezę należy odrzucić. Jeżeli jednak wartość statystyki testowej nie znajdzie się w obszarze krytycznym, a prawdopodobieństwo takiego zdarzenia jest większe niż α, to można jedynie twierdzić, że nie ma podstaw do odrzucenia weryfikowanej hipotezy.

Schemat postępowania:

1. sformułowanie hipotezy zerowej i hipotezy alternatywnej

2. ustalenie poziomu istotności α

3. wybór odpowiedniej statystyki testowej związanej z hipotezą zerową

4. określenie obszaru krytycznego

5. obliczenie wartości wybranej statystyki testowej na podstawie wyników uzyskanych z próby

6. podjęcie decyzji weryfikującej

5. TESTY ISTOTNOŚCI DLA DWÓCH ŚREDNICH. WARUNKI STOSOWANIA, SPRAWDZIANY

MODEL I

Założenia:

Losujemy dwie próby niezależne: X₁ ~ N(μ₁,σ₁) oraz X₂ ~ N(μ₂,σ₂)

σ₁,σ₂ - znane

H₀: μ₁₌μ₂

H₁: μ₁
μ₂

poziom istotności α

n₁ n₂

Sprawdzianem Hipotezy zerowej są średnie arytmetyczne
, ale wiemy, że zmienna która jest różnicą tych zmiennych:
~
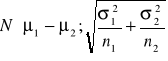
. Jeśli hipoteza H₀ jest prawdziwa, to
~
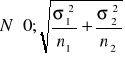
, natomiast standaryzowana statystyka postaci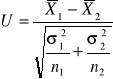
ma standaryzowany rozkład normalny N(0;1).Obszar krytyczny jest określony nierównością

MODEL II

Założenia:

Losujemy dwie próby niezależne: X₁ ~ N(μ₁,σ₁) oraz X₂ ~ N(μ₂,σ₂)

σ₁,σ₂ - nieznane, ale wiemy, że σ₁=σ₂

H₀: μ₁₌μ₂

H₁: μ₁
μ₂

poziom istotności α

n₁ n₂

Do weryfikacji hipotezy zerowej wykorzystujemy test t oparty na statystyce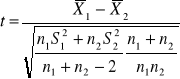
, która przy założeniu prawdziwości hipotezy zerowej ma rozkład t-Studenta o (n₁+n₂-2) stopniach swobody, gdzie S₁² i S₂² są wariancjami z prób. Obszar krytyczny jest określony nierównością

MODEL III

Założenia:

Losujemy dwie próby niezależne: X₁ ~ N(μ₁,σ₁) oraz X₂ ~ N(μ₂,σ₂)

σ₁,σ₂ - nieznane i nie wiemy czy σ₁=σ₂

H₀: μ₁₌μ₂

H₁: μ₁
μ₂

poziom istotności α

n₁ n₂

1. Musimy zweryfikować odpowiednią hipotezę o równości dwóch wariancji. W obu testach poziom istotności musi być taki sam.

2. 2.wykonujemy procedure z modelu 2 jeśli nie podstaw do odrzucenia hipotezy

H₀: σ₁²=σ₂²

MODEL IV

Założenia:

Losujemy dwie próby niezależne: X₁ ~ N(μ₁,σ₁) oraz X₂ ~ N(μ₂,σ₂)

σ₁,σ₂ - nieznane

H₀: μ₁₌μ₂

H₁: μ₁
μ₂

poziom istotności α

n₁ n₂ - duże

Sprawdzianem Hipotezy zerowej są średnie arytmetyczne
, ale wiemy, że zmienna która jest różnicą tych zmiennych:
~
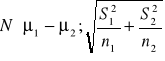
, gdzie S₁² i S₂² są wariancjami z prób. Jeśli hipoteza H₀ jest prawdziwa, to
~

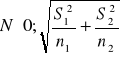
, natomiast standaryzowana statystyka postaci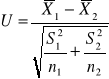
ma asymptotyczny rozkład normalny N(0;1).Obszar krytyczny jest określony nierównością

6. TEST ISTOTNOŚCI DLA DWÓCH FRAKCJI. WARUNKI STOSOWANIA, SPRAWDZIAN

MODEL

Założenia:

Losujemy dwie próby niezależne: X₁ oraz X₂ o rozkładach dwupunktowych

Z obu prób obliczamy m₁ i m₂ elementów z cechą wyróżnioną w tych próbach

p₁,p₂ - nieznane

H₀: p₁=p₂

H₁: p₁
p₂

poziom istotności α

n₁ n₂ - duże

Korzystam z twierdzenia, że w próbie rozkład różnicy miedzy wskaźnikami struktury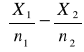
można dobrze zaproksymować za pomocą rozkładu normalnego postaci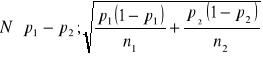
. Jeśli prawdziwa jest hipoteza zerowa to statystyka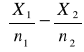
~
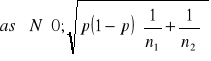
. Za ocenę p w obu populacjach przyjmuje się wskaźnik struktury z połączonych prób
. Sprawdzianem hipotezy zerowej jest

statystyka postaci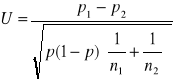
. Obszar krytyczny jest określony nierównością

7. ZWIĄZEK MIĘDZY WSPÓŁCZYNNIKIEM UFNOŚCI, A ROZPIĘTOŚCIĄ PRZEDZIAŁU UFNOŚCI

Ponieważ wraz ze wzrostem liczebności próby otrzymuje się na ogół - przy ustalonym poziomie ufności 1-α - przedziały o coraz mniejszej długości, to można stwierdzić, że wraz ze wzrostem współczynnika ufności rośnie rozpiętość przedziału ufności, a tym samym maleje precyzja oszacowania.

8. POZIOM ISTOTNOŚCI, HIPOTEZA ALTERNATYWNA, OBSZAR KRYTYCZNY. DEFINICJE, ZWIĄZKI MIĘDZY TYMI WIELKOŚCIAMI.

Hipoteza alternatywna - hipoteza przeciwna do hipotezy zerowej

Poziom istotności - prawdopodobieństwo popełnienia błędu I rodzaju, czyli odrzucenia hipotezy zerowej gdy jest ona prawdziwa. Im mniejszy przyjmie się poziom istotności α, tym

trudniej jest hipotezę zerową odrzucić. Odrzucenie hipotezy zerowej na poziomie istotności α=0,01 oznacza, że ryzyko popełnienia błędu pierwszego rodzaju przy tej decyzji wynosi 1%.

Obszar krytyczny testu - taki zbiór możliwych wartości wybranej statystyki Z_n, że zaobserwowanie w próbie losowej wartości statystyki należącej do tego zbioru będzie powodować odrzucenie sprawdzanej hipotezy zerowej.

W zależności od sformułowanej hipotezy alternatywnej wyróżnia się trzy rodzaje obszarów krytycznych:

1. dwustronny

2. prawostronny

3. lewostronny

Rozkład sprawdzianu hipotezy określa, z jakich tablic należy odczytać wartość krytyczną Z_α, wyznaczającą zbiór krytyczny.

9. TEST NIEZALEŻNOŚCI χ²

Test niezależności χ² wykorzystuje się do oceny niezależności stochastycznej dwóch cech jakościowych, dwóch cech ilościowych lub cechy jakościowej i ilościowej

Uwagi:

1. dobre ułożenie zapisu - uporządkowanie rosnąco lub malejąco

2. liczebność duża
   

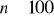
3. mały poziom istotności

4. wymaga się by liczebności oczekiwane były nie mniejsze od 5 dla każdego i, j. Ze względu na ten warunek zmniejsza się czasem liczba stopni swobody statystyki testowej, a tym samym zmniejsza się szansa odrzucenia hipotezy zerowej.

5. jeżeli dysponujemy danymi w postaci %, to należy je przekształcić w liczebności

Sprawdzianem hipotezy zerowej jest statystyka:
, która przy założeniu prawdziwości hipotezy zerowej o niezależności badanych cech, ma asymptotyczny rozkład chi-kwadrat z (r-1)(k-1) stopniami swobody. Obszar krytyczny jest prawostronny i wyznacza się go z warunku

10. TEST ZGODNOŚCI χ²

Test zgodności χ² pozwala na sprawdzenie hipotezy, że populacja generalna ma określony typ rozkładu.

1. pobieramy próbkę losową o dużej liczebności
   .

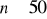
2. uzyskane z obserwacji dane przedstawiamy w postaci:

1. szeregu rozdzielczego punktowego lub przedziałowego o k wartościach x_i zmiennej X w przypadku zmiennej skokowej

2. szeregu rozdzielczego-klasowego o k klasach o środkach
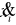
   dla zmiennej ciągłej.

3. formułujemy hipotezy:
   

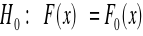
4. z teoretycznego rozkładu określonego typu obliczamy, dla każdego z możliwych wariantów cechy (klas), prawdopodobieństwa p_i, ze zmienna losowa X o określonym rozkładzie przyjmie wartości należące do wariantu cechy X o numerze i.

5. mnożymy te prawdopodobieństwa przez wielkość próby otrzymując liczebności teoretyczne.

6. obliczamy wartość statystyki testowej:
   

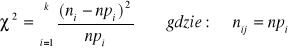
7. obszar krytyczny jest prawostronny i buduje się go na podstawie
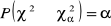
   , gdzie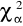
   odczytujemy z tablic rozkładu chi-kwadrat o (k-l-1) stopniach swobody, gdzie l jest liczbą parametrów rozkładu teoretycznego.

11. TEST SHAPIRO-WILKA

Test Shapiro-Wilka służy tylko i wyłącznie do sprawdzania hipotezy, że próba pochodzi ze zbiorowości o rozkładzie normalnym. Obszar odrzucenia jest lewostronny. Liczebność próby musi być duża
. W praktyce stosuje się go gdy:

1. wyraźnie jest powiedziane że dana próba pochodzi ze zbiorowości o rozkładzie normalnym

2. celem głównym jest weryfikacja hipotezy o średniej, ale wówczas statystyka testowa będzie miała rozkład t-Studenta, jeśli:

• próba pochodzi ze zbiorowości o rozkładzie normalnym

• hipoteza zerowa prawdziwa

Statystyka testowa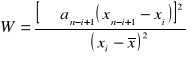
służy do sformułowania jednego z wniosków:

1. jeżeli W_obl wpadnie do obszaru krytycznego to odrzucamy hipotezę zerową

2. jeżeli W_obl >W_α to nie ma podstaw do odrzucenia hipotezy zerowej

Schemat postępowania:

1.sformułowanie hipotez statystycznych:

1. 
   

2. 
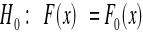
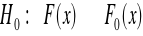
   gdzie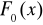
   - dystrybuanta rozkładu normalnego

2.obliczam wartość statystyki testowej W_obl

12. TESTY SERII

Testy serii stosujemy do:

1. sprawdzenia, że próba jest losowa. Obszar odrzucenia jest dwustronny
   .

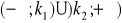
2. dwie próby pochodzą z tej samej populacji (rozkłady są jednakowe). Obszar odrzucenia jest lewostronny.

MODEL I

Schemat postępowania:

1. sformułowanie hipotez statystycznych:

1. H₀: F(x₁) = F(x₂)

2. H₁: F(x₁)
   F(x₂)

2. losujemy małą n-elementową próbę.

3. wyznaczamy medianę.

4. zaobserwowane wartości x_i∈X₁ oznaczamy jako A, zaś wartości x_i∈X₂ oznaczamy jako B

5. otrzymuję ciąg elementów a i b

6. obliczam ogólną liczbę serii k (im mniejsza jest liczba k w stosunku do liczby obserwacji n, tym większe jest prawdopodobieństwo nielosowości próby)

7. przy założeniu prawdziwości hipotezy zerowej liczba k ma znany i stablicowany rozkład zależny tylko od liczebności elementów a i b.

8. obszar krytyczny jest lewostronny
   

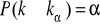
MODEL II

Schemat postępowania:

9. sformułowanie hipotez statystycznych:

1. H₀: próba jest losowa

2. H₁; próba nie jest losowa

10. losujemy małą n-elementową próbę.

11. wyznaczamy medianę.

12. zaobserwowane wartości x_i>Me oznaczamy jako A, zaś wartości x_i<Me oznaczamy jako B

13. otrzymuję ciąg elementów a i b

14. obliczam ogólną liczbę serii k (im mniejsza jest liczba k w stosunku do liczby obserwacji n, tym większe jest prawdopodobieństwo nielosowości próby)

15. przy założeniu prawdziwości hipotezy zerowej liczba k ma znany i stablicowany rozkład zależny tylko od liczebności elementów a i b.

16. obszar krytyczny jest dwustronny
    

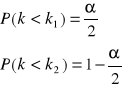
13. WERYFIKACJA HIPOTEZY O WARTOŚCI OCZEKIWANEJ W POPULACJI

MODEL I

Założenia:

Losujemy niezależnie: X ~ N(μ,σ)

σ - znane

H₀: μ₌μ₀

H₁: μ
μ₀

poziom istotności α

liczebność n

Sprawdzianem Hipotezy zerowej jest statystyka testowa postaci
, która przy założeniu prawdziwości hipotezy zerowej ma standaryzowany rozkład normalny N(0;1).Obszar krytyczny jest określony:

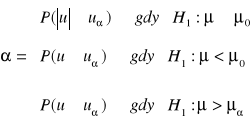
, czyli dla obszaru jednostronnego
, zaś dla obszaru odrzucenia dwustronnego

MODEL II

Założenia:

Losujemy niezależnie: X ~ N(μ,σ)

σ - nieznane

H₀: μ₌μ₀

H₁: μ
μ₀

poziom istotności α

liczebność n <30

Statystyka testowa jest postaci
i przy założeniu prawdziwości hipotezy zerowej ma rozkład t-Studenta o (n-1) stopniach swobody.

Obszar krytyczny jest określony:

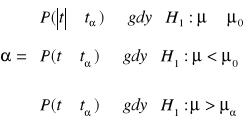
MODEL III

Założenia:

Losujemy niezależnie: X (nie ma podstaw do przyjęcia, że populacja ma rozkład normalny)

σ - nieznane

H₀: μ₌μ₀

H₁: μ
μ₀

poziom istotności α

liczebność n >30

Sprawdzianem Hipotezy zerowej jest statystyka testowa postaci
, która przy założeniu prawdziwości hipotezy zerowej ma standaryzowany rozkład normalny N(0;1).Obszar krytyczny jest określony:

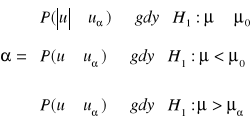
, czyli dla obszaru jednostronnego
, zaś dla obszaru odrzucenia dwustronnego

14. WERYFIKACJA HIPOTEZY O WSKAŹNIKU STRUKTURY

Założenia:

Losujemy niezależnie: X ~ rozkład dwupunktowy

H₀: p₌p₀

H₁: p
p₀

poziom istotności α

liczebność n >100

1. Wyznaczamy wskaźnik struktury z próby
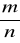
   , gdzie k - liczba elementów wyróżnionych w próbie

2. obliczamy wartość statystyki testowej
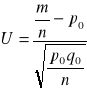
   gdzie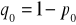
   , która przy założeniu prawdziwości hipotezy zerowej ma rozkład N(0;1)

15. WERYFIKACJA HIPOTEZY O RÓWNOŚCI WARIANCJI

Założenia:

Losujemy dwie próby niezależne: X₁ ~ N(μ₁,σ₁) oraz X₂ ~ N(μ₂,σ₂)

σ₁,σ₂ - nieznane

poziom istotności α

n₁ n₂

Hipotezy:

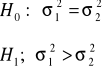
Statystyka testowa ma postać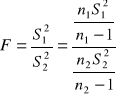
i ma ona przy założeniu prawdziwości hipotezy zerowej rozkład F Snedecora o (n₁-1) i (n₂-1) stopniach swobody. Obszar odrzucenia jest prawostronny.

Hipotezy statystyczne i ich weryfikacja testy statystyczne

- 4 -

---