HIPOTEZY

STATYSTYCZNE

HIPOTEZY

STATYSTYCZNE

Hipotezami statystycznymi określa się każde

przypuszczenie dotyczące rodzaju rozkładu zmiennej

losowej

(wtedy

mówimy

o

hipotezach

nieparametrycznych) lub jego parametrów (hipotezy

parametryczne). Najczęściej spotykane w praktyce

hipotezy statystyczne mają postać:

   Wartość oczekiwana lub wariancja cechy populacji

ogólnej jest równa pewnej liczbie (mniejsza od pewnej

liczby, większa od pewnej liczby).

   Wartości oczekiwane (wariancje lub inne parametry)

dwóch populacji są równe; wartość oczekiwana w

populacji

pierwszej

jest

większa

od

wartości

oczekiwanej w populacji drugiej.

HIPOTEZY

STATYSTYCZNE

Wśród hipotez statystycznych wyróżniamy hipotezy zerowe H

0

oraz hipotezy alternatywne H

1

. Hipotezę dopuszczalną,

podlegającą sprawdzeniu (weryfikacji) nazywa się hipotezą

zerową.Każdą

dopuszczalną hipotezę poza hipotezą zerową

nazywa się alternatywną.

Przykład: Interesuje nas wartość oczekiwana zmiennej losowej X,
czyli EX = m, która jest parametrem nieznanym. Sformułowanie
hipotezy zerowej może być następujące:

H

0

: EX = m

0

Hipotezy alternatywne mogą mieć postać:

H

1

: EX < m

0

lub

H

1

: EX  m

0

lub

H

1

: EX > m

0

HIPOTEZY

STATYSTYCZNE

Wnioskowanie statystyczne polega na orzeczeniu, czy

hipoteza jest słuszna czy też nie, po uzyskaniu
odpowiednich informacji z próby. Postępowanie takie
nazywa się weryfikacją lub testowaniem hipotezy.
Statystyczna procedura weryfikacji hipotez zerowych oparta
jest na specjalnych narzędziach zwanych testami. Przez test
statystyczny rozumiemy postępowanie statystyczne, w
którego wyniku przyjmujemy lub odrzucamy weryfikowaną
hipotezę statystyczną. W zależności od rodzaju hipotezy
zerowej możemy wyróżnić testy zgodności (użyteczne do
weryfikacji nieparametrycznych H

0

) oraz testy istotności

(użyteczne do weryfikacji parametrycznych H

0

).

Przyjęcie lub odrzucenie hipotezy zerowej może być

obarczone błędem. Przyjmuje się że błąd jest pierwszego
rodzaju, jeżeli została odrzucona hipoteza zerowa, podczas
gdy w rzeczywistości jest ona prawdziwa.Błędem drugiego
rodzaju nazywa się błąd polegający na przyjęciu hipotezy
zerowej podczas gdy w rzeczywistości jest ona fałszywa.

HIPOTEZY

STATYSTYCZNE

W postępowaniu badawczym związanym z weryfikacją hipotez

statystycznych wyodrębnić można cztery etapy:

  Etap I, w którym formułowana jest właściwa hipoteza zerowa

oraz ewentualnie odpowiadająca jej hipoteza alternatywna.

Etap II, w którym wybierany jest – odpowiedni do

sformułowanej hipotezy zerowej – test zgodności lub istotności.
Polega to na wyborze odpowiedniej funkcji testowej (jest to
zmienna losowa: normalna standaryzowana, t – Studenta lub
inna, która jest funkcją charakterystyk próby takich jak:
liczność próby , wartość średnia , wariancja z próby , czasami
także parametrów populacji: wartość oczekiwana lub
odchylenie standardowe). Stosując funkcję testową wyliczamy
wartość liczbową tego testu dla danej próby.

HIPOTEZY

STATYSTYCZNE

Etap III, w którym przyjmowany jest poziom

istotności  i wyznaczane są obszary

krytyczne hipotezy zerowej. Obszar krytyczny

jest to zbiór tych wartości funkcji testowej, dla

których hipotezę H

0

odrzucamy.Wartości

statystyki przynależne do brzegu obszaru

krytycznego

nazywane

są

wartościami

krytycznymi.Każdemu obszarowi krytycznemu

odpowiada określone prawdo-podobieństwo

popełnienia

błędów.Prawdopodobieństwo

popełnienia błędu pierwszego rodzaju nazywa

się poziomem istotności i oznacza literą

alfa.Zwykle przyjmuje się  równe 5%, 1% lub

0,1%.

Etap IV, w którym podejmowana jest – na

ustalonym poziomie istotności – decyzja

odrzucenia (wtedy, kiedy wartość testu

zawiera się w obszarze krytycznym) lub

nieodrzucenia (wtedy, gdy wartość testu jest

poza obszarem krytycznym) danej hipotezy

zerowej.

Test istotności dla wartości

oczekiwanej

 

Testować będziemy 3 warianty hipotez H

0

i H

a

1)      H

0

: =

0

; H

a

: =

1



0

2)      H

0

: =

0

; H

a

: =

1

<

0

3)      H

0

: =

0

; H

a

: =

1

>

0

W przypadku, gdy weryfikację opieramy na dużej próbie

(n>30) i znane są parametry populacji, najwygodniejszą
funkcją testową jest średnia standary-

zowana

n

x

u









n

S

x

t

x

0







W przypadku, gdy weryfikację opieramy na małej próbie
(n<30) i nieznane są

parametry rozkładu, to statystyką testową będzie

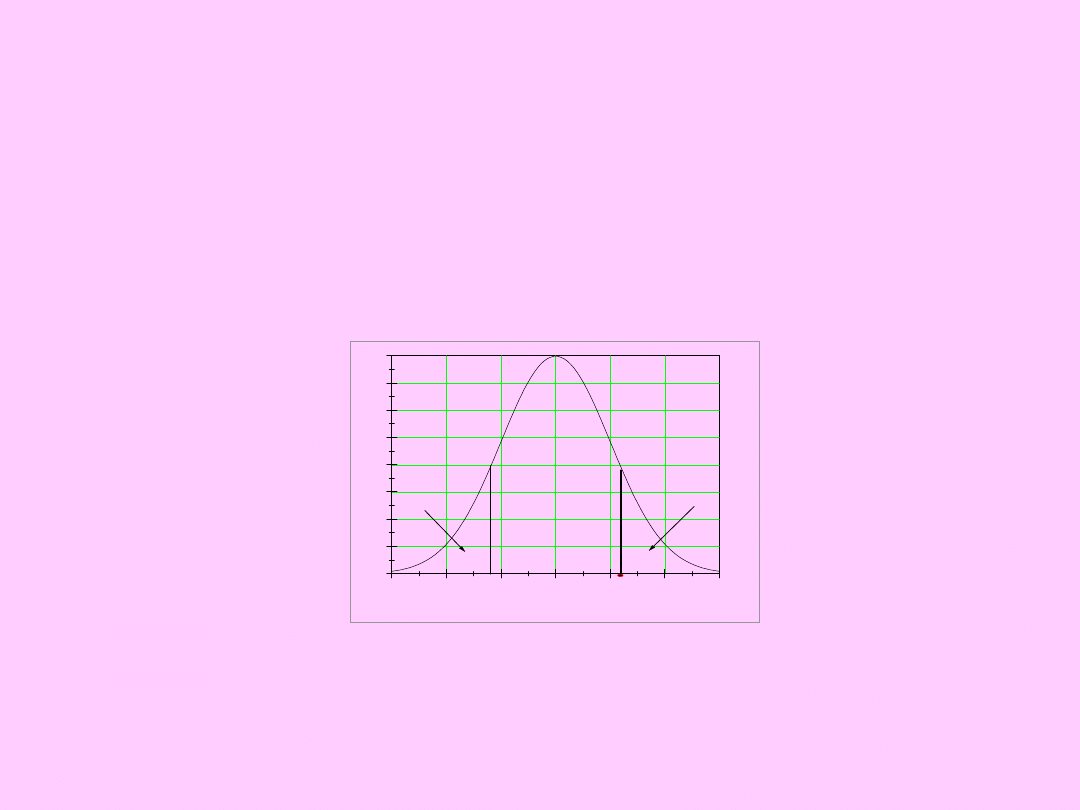
Test istotności dla wartości

oczekiwanej

1)      H

0

: =

0

; H

a

: =

1



0

-3

-2

-1

0

1

2

3

0.00

0.05

0.10

0.15

0.20

0.25

0.30

0.35

0.40

-t

n,

t

n,



/2



/2

1-



Dwustronny obszar
krytyczny
(odrzuć H

0

na korzyść H

a

)

(-, -t

n,

), (t

n,

, +

)

 

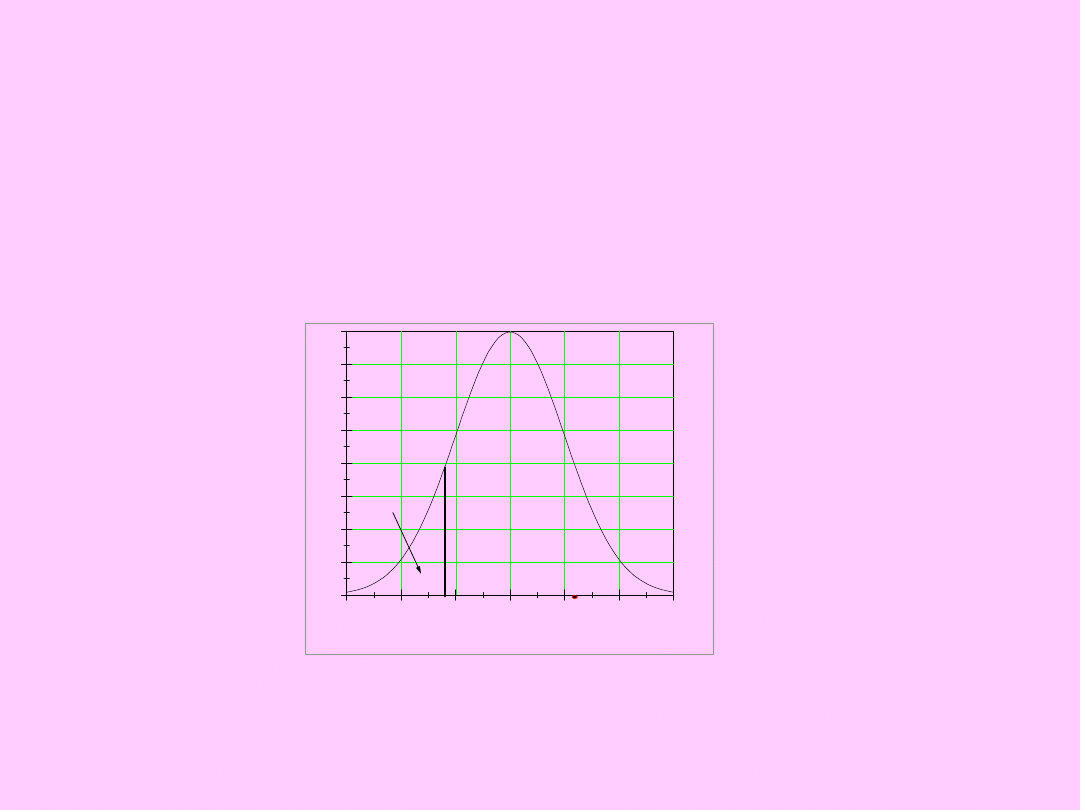
Test istotności dla wartości

oczekiwanej

2) H

0

: =

0

; H

a

: =

1

<

0

-3

-2

-1

0

1

2

3

0.00

0.05

0.10

0.15

0.20

0.25

0.30

0.35

0.40

-t

n,



t

n,





1-



Jednostronny obszar
krytyczny
(odrzuć H

0

na korzyść H

a

)

(-, -t

n,

)

 

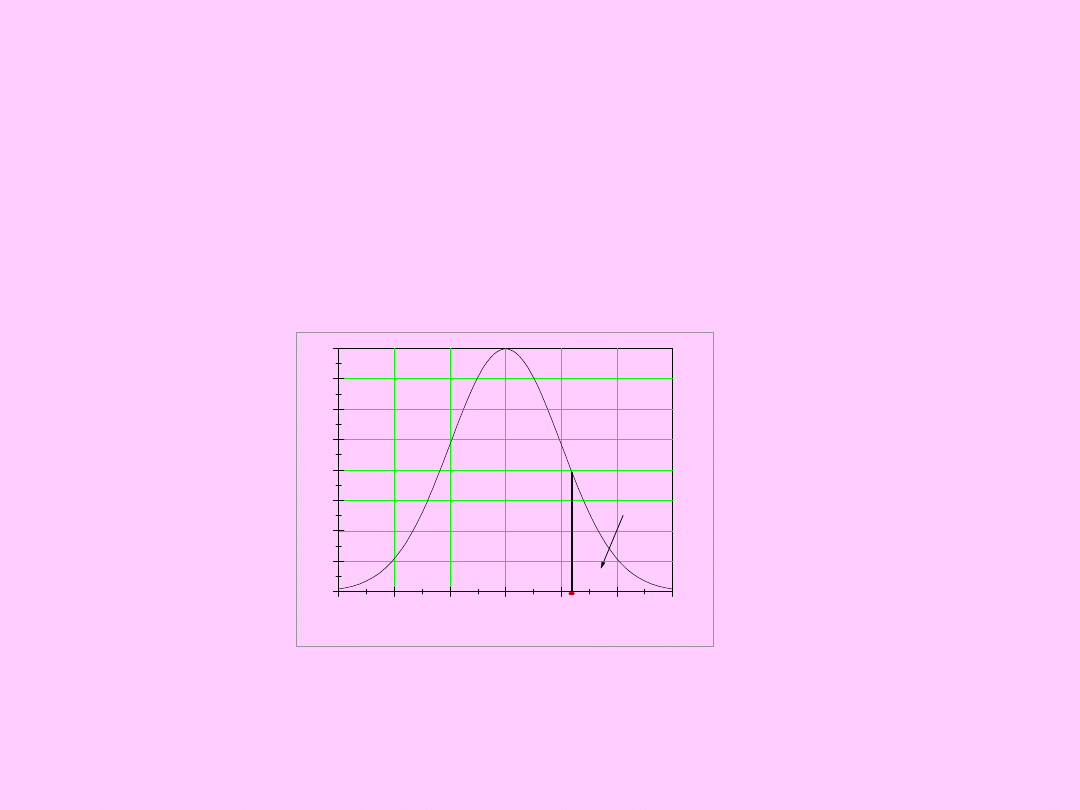
Test istotności dla wartości

oczekiwanej

3) H

0

: =

0

; H

a

: =

1

>

0

-3

-2

-1

0

1

2

3

0.00

0.05

0.10

0.15

0.20

0.25

0.30

0.35

0.40

-t

n,



t

n,





1-



Jednostronny obszar
krytyczny
(odrzuć H

0

na korzyść H

a

)

(t

n,

, +

)

Testy

parametryczne

Testy parametryczne pozwalają formułować
szereg wniosków dotyczących różnych
parametrów statystycznych.

Badanie zjawisk

w drodze obliczania wybranych parametrów
jest bardzo efektywnym sposobem poznania,
wynika to ze zwięzłej i precyzyjnej formy
opisu. Jednak testy parametryczne, mimo
swej różnorodności, nie dają odpowiedzi na
wszystkie istotne pytania, głównie dlatego, że
testy te mogą być stosowane w przypadku,
gdy badana wielkość (populacja) ma rozkład
normalny lub bardzo zbliżony do niego.
Ponadto testy parametryczne, jak sama
nazwa wskazuje, opisują pewną właściwość
badanego zjawiska (wyników pomiarów), nie
dając dostatecznych podstaw do
formułowania wniosków ogólnych.

Przy budowie każdego testu należy uchronić
się zarówno przed popełnieniem

błędu

pierwszego rodzaju, polegającego na
odrzuceniu hipotezy prawdziwej,

jak i

popełnieniem

błędu drugiego rodzaju,

polegającego na przyjęciu hipotezy
fałszywej

.

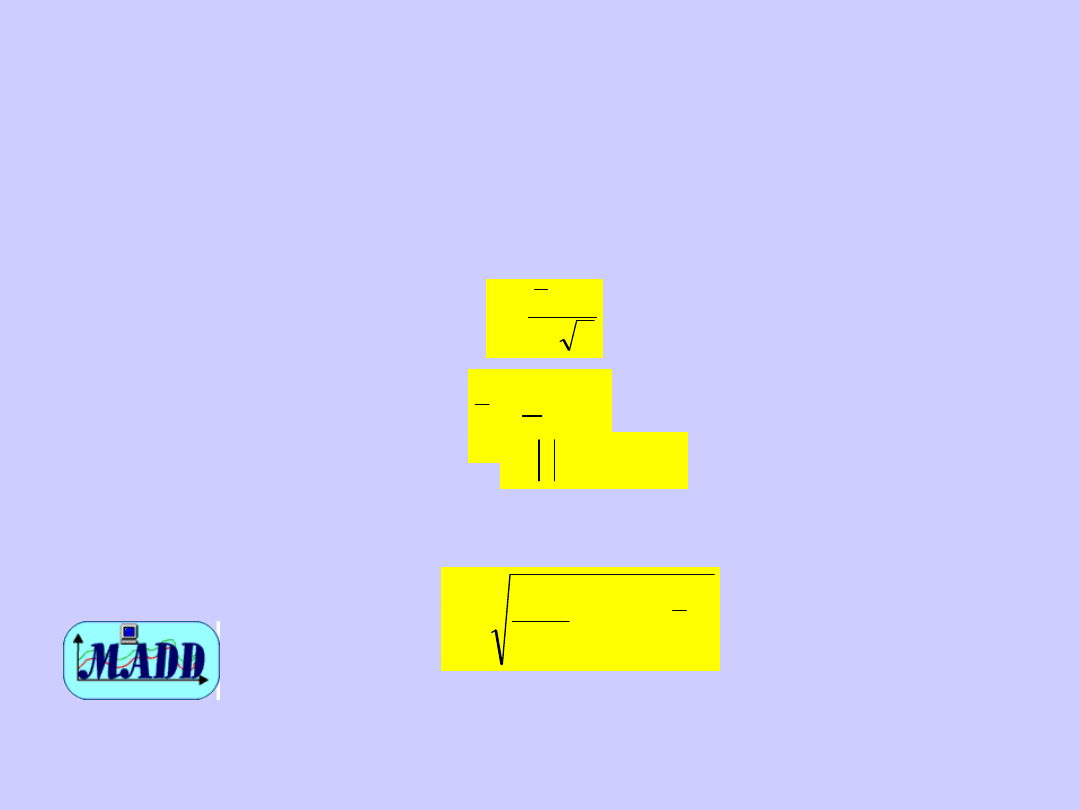
Test t Studenta

Test zgodności średniej próby ze średnią populacji

Za pomocą tego testu możemy
sprawdzić hipotezę zerową
postaci:
H

0

:  = 

0

natomiast hipoteza
alternatywna ma postać:
H

1

:   

0

W praktyce rzadko znamy wartość średnią i
odchylenie standardowe populacji generalnej,
musimy więc zadowolić się szacunkiem tych
wielkości za pomocą najczęściej stosowanych
estymatorów - wartości średniej z próby:

i odchylenia standardowego na podstawie próby
obliczonego w oparciu o wzór:







n

i

i

x

n

x

1

1















n

i

i

x

x

n

s

1

2

1

1

Obliczamy statystykę:

która ma rozkład t Studenta o n - 1
stopniach swobody (n oznacza liczbę
próbek), pod warunkiem, że populacja ma
rozkład normalny lub bardzo zbliżony do
niego.

n

s

x

t

/







Zatem, gdy chcemy sprawdzić hipotezę
zerową o równości średniej wartości dla
próby ze średnią wartością dla populacji,
korzystamy z tablic rozkładu t Studenta i dla
założonego poziomu ufności  odczytujemy
wartość krytyczną t



, taką, że:

Następnie porównujemy wartość krytyczną z
obliczoną wartością t i jeżeli:
 |t|  t



wówczas odrzucamy hipotezę

zerową;
 |t| < t



wtedy nie ma podstaw do odrzucenia

hipotezy zerowej.











t

t

P

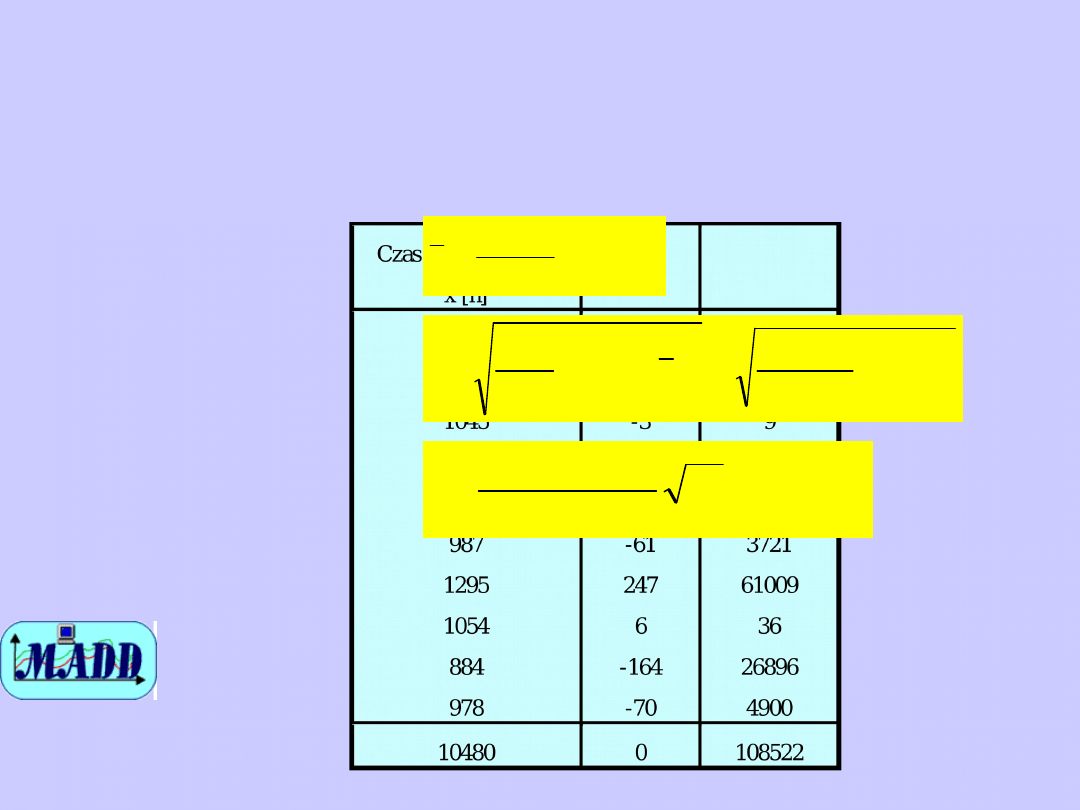
Test t Studenta

Przykład

Wiemy, że średni czas świecenia
żarówki wynosi 

0

= 1059 godzin. Po

wprowadzeniu zmian w technologii
postanowiono sprawdzić, czy zmiany te
nie skróciły czasu świecenia. Hipoteza
zerowa ma zatem postać H



: 

1

= 



,

czyli: średni czas świecenia żarówki nie
uległ zmianie. Do badania pobrano
losowo próbę 10 żarówek, wyniki tych
badań przedstawia tabela.

h

x

1048

10

10480









8

.

109

9

108522

1

1

1

2















n

i

i

x

x

n

s

317

,

0

10

8

.

109

1059

1048









t

Odczytana z tablic dla poziomu
istotności 0,1 wartość krytyczna t



=

1,833, zatem nie ma podstaw, aby
postawioną hipotezę zerową
odrzucić.

Porównanie dwóch

wartości oczekiwanych

Często zachodzi konieczność

porównania wyników dwóch prób i
odpowiedzenia na pytanie, czy
pochodzą one z tej samej popu-lacji
generalnej, co formalnie zapisujemy
w postaci hipotezy zerowej H

0

: 

1

=



2

. Dla małych prób o nieznanej

wariancji funkcją testową może być
zmienna losowa t Studenta.

Porównanie dwóch

wartości oczekiwanych

Można udowodnić następujące twierdzenie:
Jeżeli mamy dwie próby wylosowane z populacji o takiej

samej wariancji  : próbę I o liczebności n

1

pochodzącą (z

populacji o rozkładzie N(

1

, ) i próbę II o liczebności n

2

pochodzącą z populacji o rozkładzie N(

2

, ), to zmienna

losowa

2

1

2

1

2

1

2

2

2

2

1

1

2

1

)

2

(

)

1

(

)

1

(

n

n

n

n

n

n

S

n

S

n

x

x

t

















ma rozkład Studenta o (n

1

+n

2

-2) stopniach swobody. W tym wzorze S

2

oznacza
wariancję z próby.

Jeśli wartość obliczona t okaże się większa od wartości
krytycznej stwierdzimy podstawy do odrzucenia
hipotezy zerowej. Jeśli natomiast wartość obliczona
będzie mniejsza - nie będzie podstaw do odrzucenia
hipotezy zerowej.

Testy

nieparametryczne

Testy nieparametryczne
są uniezależnione od
rozkładu badanej cechy,
mogą być więc stosowane
także w przypadku
dowolnych rozkładów,
niekoniecznie zbliżonych
do normalnego.

Testy nieparametryczne
możemy podzielić na dwie
grupy:

• testy zgodności, pozwalające
na sprawdzenie hipotezy, że
populacja ma określony typ
rozkładu,

• testy dla hipotezy, że dwie
próby pochodzą z jednej
populacji (czyli, że dwie
populacje mają ten sam
rozkład).

Test zgodności chi-

kwadrat

Jest to jeden z najstarszych testów
statystycznych, pozwalający na
sprawdzenie hipotezy, że populacja
ma określony typ rozkładu (opisany
pewną dystrybuantą w postaci
funkcji), przy czym może to być
zarówno rozkład ciągły lub skokowy.
Jedynym ograniczeniem jest to, że
próba musi być duża, zawierająca co
najmniej kilkadziesiąt próbek,
bowiem wyniki jej musimy podzielić
na pewne klasy wartości. Klasy te nie
powinny być zbyt mało liczne, do
każdej z nich powinno wpadać
przynajmniej po 8 wyników.

Sposób postępowania jest następujący:
1.

Wyniki dzielimy na r rozłącznych klas

o liczebnościach n

i

, przy czym liczebność

próby

otrzymując w ten sposób rozkład
empiryczny.
2.

Formułujemy hipotezę zerową, że

badana populacja ma rozkład o
dystrybuancie należącej do pewnego zbioru
rozkładów o określonym typie postaci
funkcyjnej dystrybuanty;





r

i

i

n

n

3.

Z hipotetycznego rozkładu obliczamy

dla każdej z r klas wartości badanej zmiennej
losowej X prawdopodobieństwa p

i

, że zmienna

losowa przyjmie wartości należące do klasy o
numerze i (i = 1,2,...,r);
4.

Obliczamy liczebności teoretyczne

np

i

, które powinny wystąpić w klasie i, gdyby

populacja miała założony rozkład;

5.

Ze wszystkich liczebności

empirycznych n

i

oraz hipotetycznych np

i

wyznaczmy wartość statystyki:

która, przy założeniu prawdziwości hipotezy
zerowej, ma rozkład chi-kwadrat o r - 1
stopniach swobody lub o r - k - 1 stopniach
swobody, gdy z próby oszacowano k
parametrów rozkładu;











r

i

i

i

i

np

np

n

x

2

2

6. Z tablicy rozkładu chi-kwadrat dla
ustalonego poziomu ufności odczytuje się
taką wartość krytyczną aby zachodziło P( )
= 1 - .

7. Porównujemy obie wartości i jeśli
zachodzi nierówność

to hipotezę należy odrzucić. W przeciwnym
przypadku, gdy

nie ma podstaw do odrzucenia hipotezy
zerowej, nie oznacza to jednak, że możemy
ją przyjąć.

2

2









2

2









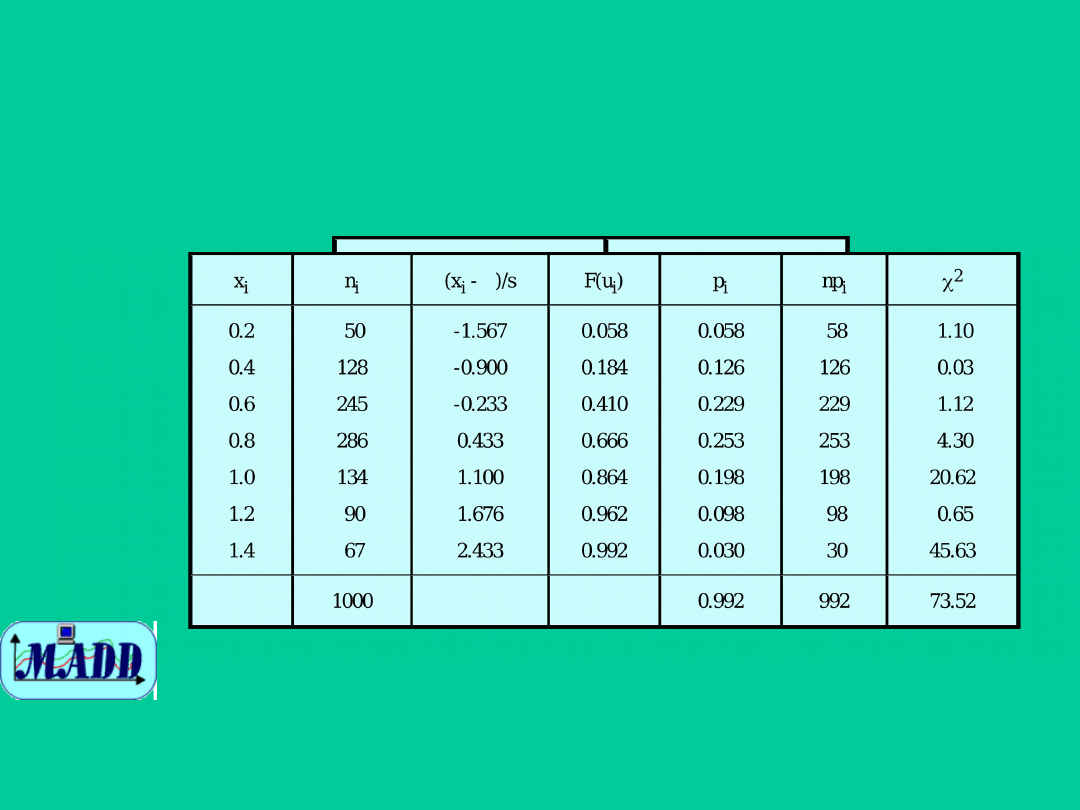
Test zgodności chi-

kwadrat

W pewnym doświadczeniu fizycznym
mierzy

się

czas

rozbłysku.

Przeprowadzono

n

=

1000

niezależnych doświadczeń nad tym
efektem i zbiór pogrupowanych
wyników jest taki jak w tabeli.
Na poziomie ufności 99% należy
zweryfikować

hipotezę,

że

czas

występowania badanego w tych
doświadczeniach efektu świetlnego
ma rozkład normalny. Z treści zadania
nie wynikają parametry rozkładu
hipotetycznego.

Nasza

hipoteza

zerowa zatem będzie brzmiała: F(x) 

 gdzie  jest klasą wszystkich

dystrybuant normalnych.

Przykład

Dwa parametry rozkładu, średnią
wartość m i odchylenie standardowe
, szacujemy z próby za pomocą

estymatorów m = 0.67 i s = 0.30.
Dalsze wyniki zestawiamy w tabeli,
gdzie F(u

i

) jest wartością

dystrybuanty rozkładu normalnego
N(0,1) w punkcie u

i

= (x

i

-m) / s,

który jest standaryzowaną wartością
prawego końca przedziału
klasowego.

Liczba stopni swobody k = 7 - 2 - 1
= 4, gdyż na podstawie próby
losowej zostały policzone dwa
parametry: wartość średnia i
odchylenie standardowe. Z tablic
rozkładu chi-kwadrat, dla poziomu
istotności 0,01, znajdujemy wartość
krytyczną = 13,277. Wartość
krytyczna jest mniejsza od obliczonej
statystyki równej 73,52, zatem
hipotezę o normalności rozkładu
należy odrzucić.

Test zgodności 

Kołmogorowa

W teście zgodności  Kołmogorowa, dla

zweryfikowania hipotezy, że populacja ma
określony typ rozkładu, nie rozpatruje się, jak w
teście chi-kwadrat, liczebności szeregu
empirycznego i porównuje z liczebnościami
szeregu hipotetycznego, ale porównuje się
dystrybuantę empiryczną i hipotetyczną. Bowiem,
gdy populacja ma rozkład zgodny z hipotezą, to
wartości dystrybuanty empirycznej i hipotetycznej
powinny być we wszystkich badanych punktach
zbliżone.

Test rozpoczynamy od zanalizowania różnic

między tymi dwoma dystrybuantami, największa z
nich posłuży następnie do budowy statystyki
lambda, której rozkład nie zależy od postaci
dystrybuanty hipotetycznej. Rozkład ten określa
wartości krytyczne w tym teście. Jeżeli
maksymalna różnica w pewnym punkcie obszaru
zmienności badanej cechy jest zbyt duża, to
hipotezę, że rozkład populacji ma taką
dystrybuantę jak przypuszczamy, należy odrzucić.

Stosowanie tego testu jest jednak

ograniczone, dystrybuanta hipotetyczna
musi bowiem być ciągła, w zasadzie
powinniśmy też znać parametry tego
rozkładu, jednak w przypadku dużych
prób możemy je szacować na podstawie
próby

.

Sposób postępowania w teście
Kołmogorowa jest następujący:
1. porządkujemy wyniki w kolejności
rosnącej lub grupujemy je w
stosunkowo wąskie przedziały, o
prawych końcach x

i

i odpowiadających

im liczebnościach n

i

;

2. wyznaczamy dla każdego x

i

wartość

empirycznej dystrybuanty F

n

(x)

korzystając ze wzoru:

 







k

i

i

k

n

n

n

x

F

1

1

3. z rozkładu hipotetycznego wyznaczamy dla
każdego x

i

wartość teoretycznej dystrybuanty

F(x);
4. dla każdego x

i

obliczamy wartość

bezwzględną różnicy F

n

(x)-F(x);

5. obliczamy wartość statystyki D = sup|
F

n

(x)-F(x)| oraz wartość statystyki:

która, przy prawdziwości hipotezy zerowej,
powinna mieć rozkład Kołmogorowa.

n

D





6. dla ustalonego poziomu
ufności  odczytujemy z

granicznego rozkładu
Kołmogorowa wartość krytyczną
spełniającą warunek P{  

kr

}

= 1 - .

Gdy   

kr

hipotezę zerową

należy odrzucić, w przeciwnym
wypadku nie ma podstaw do
odrzucenia hipotezy zerowej.