FORMUŁOWANIE

FORMUŁOWANIE

HIPOTEZ

HIPOTEZ

STATYSTYCZNYCH

STATYSTYCZNYCH

FORMUŁOWANIE

FORMUŁOWANIE

HIPOTEZ

HIPOTEZ

STATYSTYCZNYCH

STATYSTYCZNYCH

Porównanie średniej odległości

rzutu kulą

0

5

10

15

20

25

Grupa zawodników

Grupa studentów

O

d

le

g

ło

ść

[

m

]

Porównanie średniej odległości

rzutu kulą

0

5

10

15

20

25

Grupa zawodników

Grupa studentów

O

d

le

g

ło

ść

[

m

]

HIPOTEZA

HIPOTEZA

• Zdanie nie w pełni uzasadnione,

wymagające sprawdzenia. Hipotezy
naukowe powstają zwykle wtedy, gdy
dla pewnych faktów nie znajduje się
racji wśród uznanych twierdzeń.

• Celem formułowania hipotez jest

odkrycie nieznanych zjawisk lub
praw.

Weryfikacja hipotezy

Weryfikacja hipotezy

• Eksperyment jest zabiegiem

badawczym polegającym na celowym
wywołaniu zjawiska (lub jego zmiany)
w celu zweryfikowania sformułowanej
uprzednio hipotezy.

• Hipoteza w wyniku eksperymentu

może zostać potwierdzona (wzrasta
jej prawdopodobieństwo) lub obalona.

Falsyfikacja

Falsyfikacja

• procedura mająca na celu wykazanie

fałszywości (błędności ) sformułowanej
hipotezy i prowadząca do jej odrzucenia.

• Odrzucenie hipotezy na podstawie kolejnej

obserwacji jest zabiegiem z logicznego
punktu widzenia ostatecznym.
Uprawdopodobnienie hipotezy na
podstawie kolejnej obserwacji nie
wyklucza, że dalsze obserwacje
doprowadzą do jej odrzucenia.

Przykład

Przykład

•

Hipoteza:

Hipoteza: wszystkie kruki są czarne

wszystkie kruki są czarne

• 1 kruk - czarny (zgadza się),
• 2 kruk - czarny (kolejne potwierdzenie),
• ...
• 127 kruk - czarny (już jesteśmy prawie

pewni),

• 128 kruk - biały (i po ptakach - hipoteza

zostaje odrzucona).

Formułowanie hipotezy

Formułowanie hipotezy

statystycznej

statystycznej

• Hipoteza zerowa: efekt, który nas

efekt, który nas

interesuje, a który, jak nam się

interesuje, a który, jak nam się

wydaje, obserwujemy jest jedynie

wydaje, obserwujemy jest jedynie

wynikiem przypadkowym.

wynikiem przypadkowym.

• Weryfikacja: jeżeli możemy wykazać, że

hipoteza zerowa jest bardzo mało
prawdopodobna odrzucamy ją. W
przeciwnym przypadku nie odrzucamy
hipotezy, co oczywiście nie oznacza jej
przyjęcia.

Poziom istotności

Poziom istotności

• Co to znaczy, że hipoteza jest mało

prawdopodobna?
Graniczne prawdopodobieństwo dobieramy
arbitralnie. Zwykle przyjmuje się, że
prawdopodobieństwo prawdziwości
hipotezy zerowej p<0,05 (5%) jest
wystarczająco małe żeby ją odrzucić.

• Graniczne prawdopodobieństwo nazywamy

poziomem istotności i oznaczamy przez 



.

Dobór poziomu

Dobór poziomu

istotności

istotności

• Zwykle przyjmuje się jedną z trzech

wartości 



: 0,05

0,05

; 0,01

0,01

lub 0,001

0,001

.







= 0,05 - badania na mało licznych

próbkach, gdy pomyłka nie powoduje
groźnych skutków,







= 0,01 - badania, w których zależy nam

na uzyskaniu wiążących wyników,







= 0,001 - badania, w których pomyłka

może spowodować groźne skutki
(testowanie leków, uzbrojenia itp.)

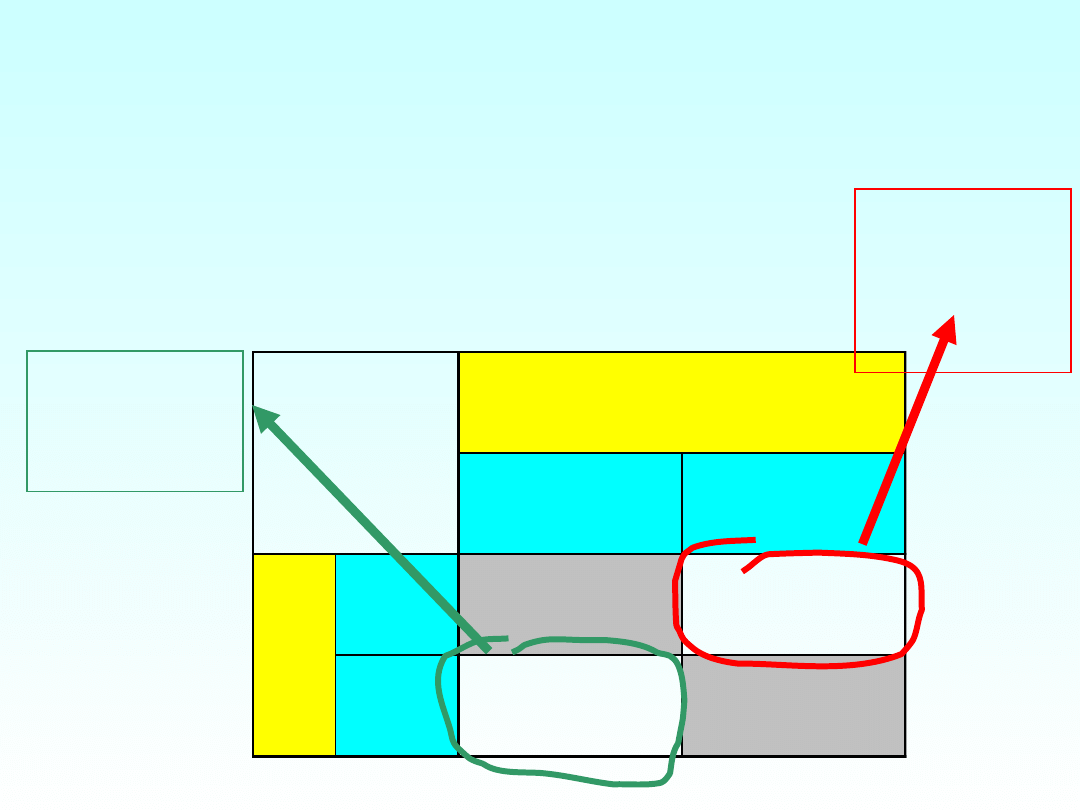
Błędy wnioskowania

Błędy wnioskowania

Hipoteza zerowa:

testowany efekt nie

testowany efekt nie

występuje

występuje

Ogłaszam
y
nieprawdę

nie występuje

występuje

nie
wystepuje

nie odrzucamy OK.

nie odrzucamy

-

popełniamy błąd II
rodzaju

występuje

odrzucamy

-

popełniamy błąd I
rodzaju

odrzucamy OK.

stan faktyczny

st

a

n

o

rz

e

cz

o

n

y

Jesteśmy
tak samo
głupi jak
przedtem

Błędy wnioskowania

Błędy wnioskowania

•

Błąd I rodzaju

Błąd I rodzaju

:

niesłusznie odrzucamy hipotezę zerową,
ogłaszamy istnienie efektu, którego w
rzeczywistości nie ma.

•

Błąd II rodzaju

Błąd II rodzaju

:

Nie odrzucamy hipotezy zerowej, nie
wykrywamy efektu, który w
rzeczywistości zachodzi.

Poziom istotności a

Poziom istotności a

błędy wnioskowania

błędy wnioskowania

• Prawdopodobieństwo prawdziwości

hipotezy zerowej to prawdopodobieństwo
popełnienia błędu I rodzaju.

• Maksymalne, przyjęte jako dopuszczalne,

prawdopodobieństwo popełnienia błędu I
rodzaju to poziom istotności 



.

• Błędu drugiego rodzaju nie da się

określić w sposób ścisły.

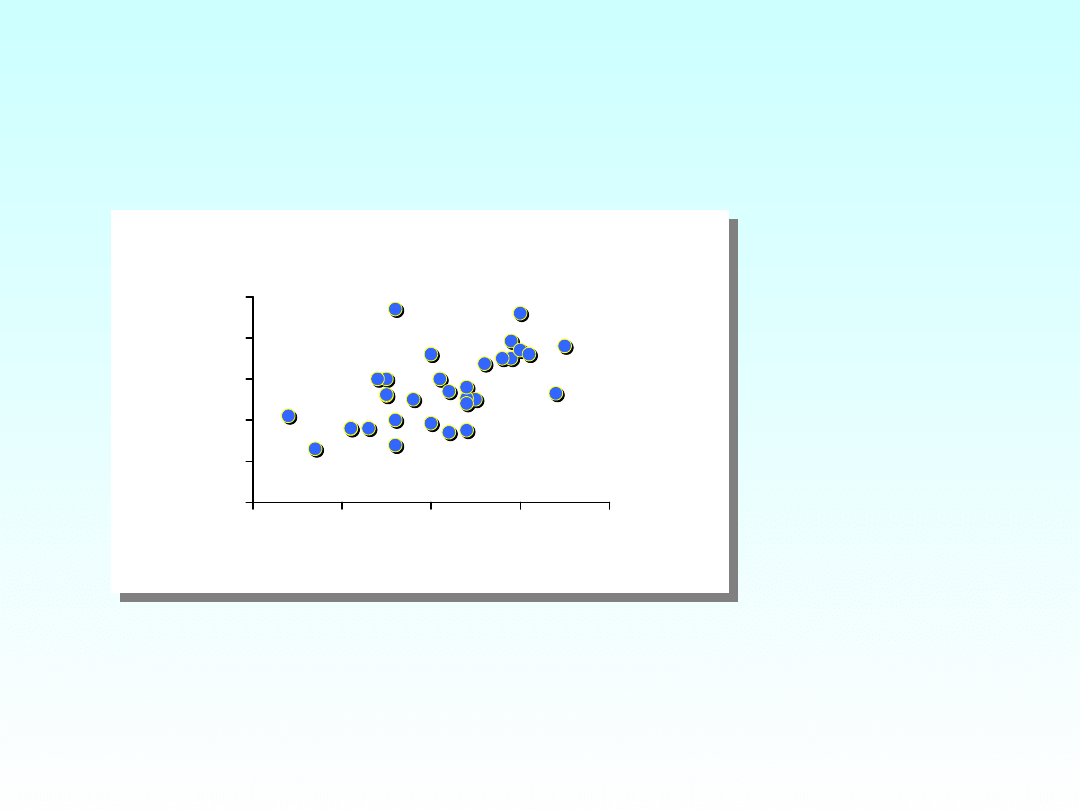
H

H

0

0

: związek między dwiema

: związek między dwiema

zmiennymi mierzalnymi nie

zmiennymi mierzalnymi nie

zachodzi

zachodzi

Związek masy ciała z wysokością

50

60

70

80

90

100

160

170

180

190

200

Wysokość [cm]

M

a

sa

[

k

g

]

Związek masy ciała z wysokością

50

60

70

80

90

100

160

170

180

190

200

Wysokość [cm]

M

a

sa

[

k

g

]

Jeżeli wykażemy, że prawdopodobieństwo
przypadkowego ułożenia punktów w sposób
wskazujący na istnienie związku jest małe -
odrzucamy H

0

Punktowy,

Punktowy,

dwuwymiaro

dwuwymiaro

wy wykres

wy wykres

rozrzutu

rozrzutu

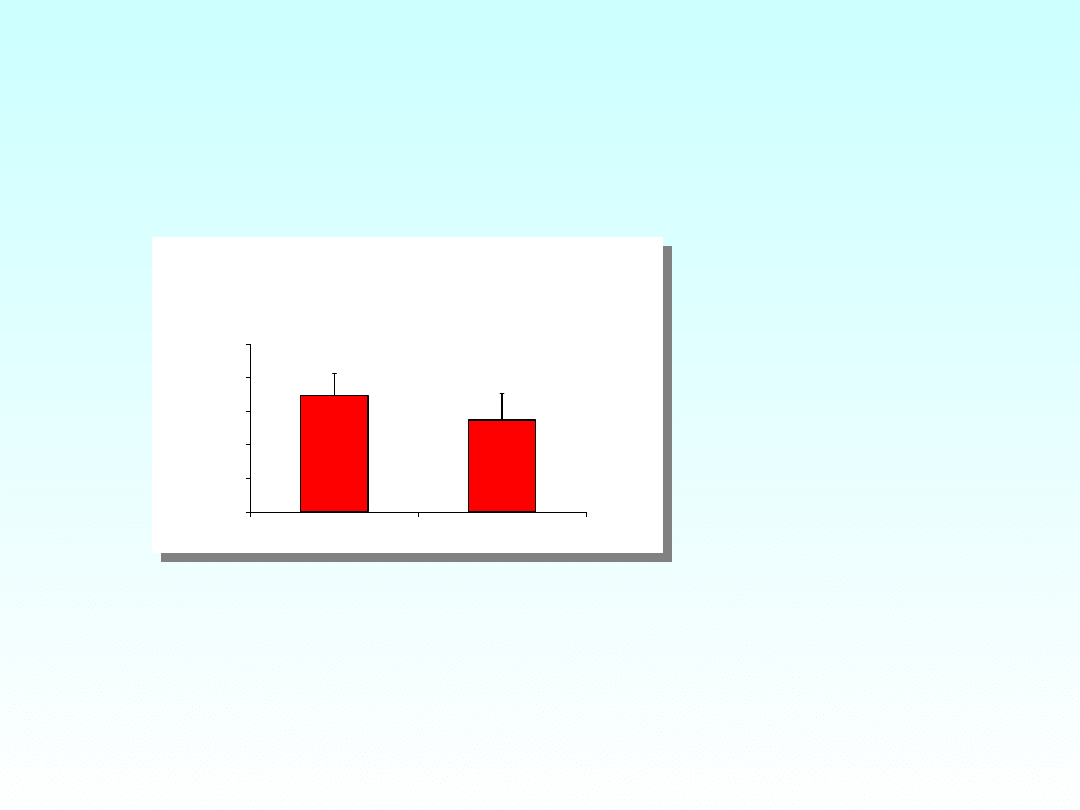
H

H

0

0

: Średnie wartości cechy w

: Średnie wartości cechy w

dwóch grupach nie różnią się

dwóch grupach nie różnią się

od siebie

od siebie

Histogramy z

Histogramy z

zaznaczonymi

zaznaczonymi

wartościami

wartościami

odchyleń

odchyleń

standardowyc

standardowyc

h

h

Jeżeli wykażemy, że prawdopodobieństwo
przypadkowego charakteru różnicy średnich jest
małe - odrzucamy H

0

Porównanie średniej odległości

rzutu kulą

0

5

10

15

20

25

Grupa zawodników

Grupa studentów

O

d

le

g

ło

ść

[

m

]

Porównanie średniej odległości

rzutu kulą

0

5

10

15

20

25

Grupa zawodników

Grupa studentów

O

d

le

g

ło

ść

[

m

]

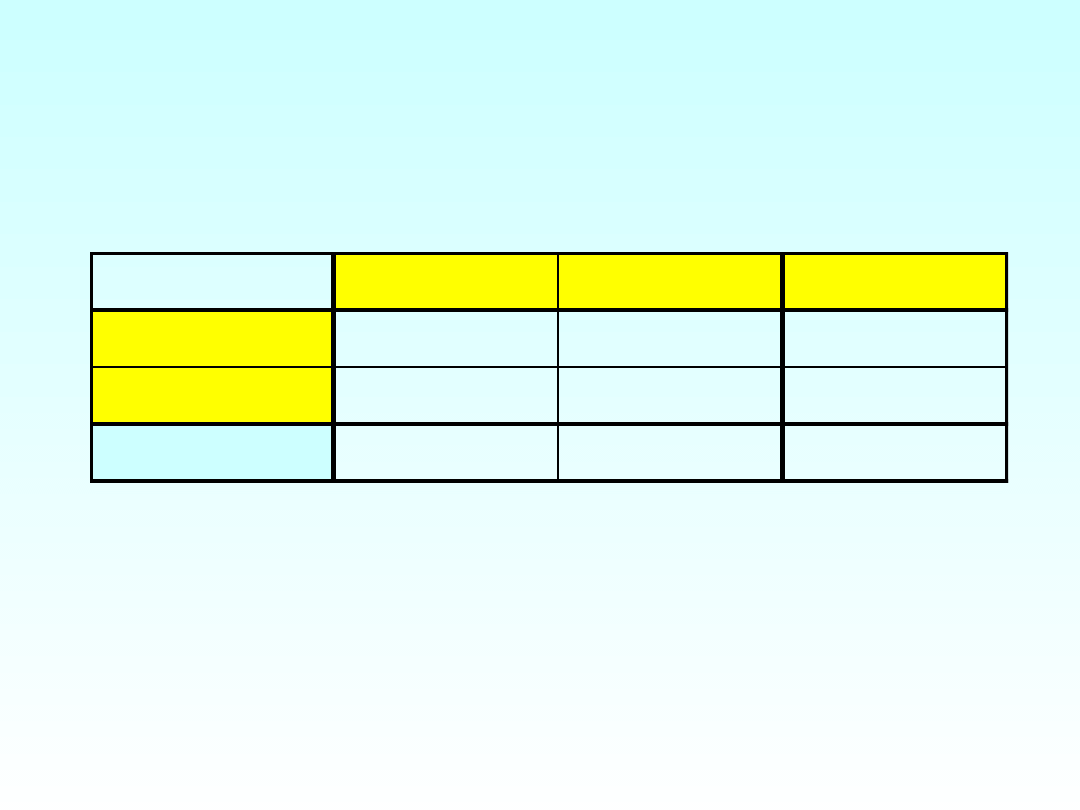
H

H

0

0

: Frakcje tych, którzy lubią

: Frakcje tych, którzy lubią

szpinak są jednakowe wśród

szpinak są jednakowe wśród

kobiet i mężczyzn

kobiet i mężczyzn

KOBIETY

MĘŻCZYŹNI

RAZEM

LUBI SZPINAK

34

56

90

NIE LUBI SZPINAKU

24

67

91

RAZEM

58

123

181

59%

46%

Jeżeli wykażemy, że prawdopodobieństwo
przypadkowego charakteru różnicy frakcji jest
małe - odrzucamy H

0

Algorytm postępowania

Algorytm postępowania

1. Sformułowanie H

0

, dobranie 



2. Obliczenie wskaźnika

statystycznego służącego do
oceny prawdopodobieństwa (P)
błędu I-go rodzaju (t-Studenta, 

2

itp.)

3. Jeżeli P<



odrzucamy H

o

,

w przeciwnym przypadku (P>=



)

nie odrzucamy H

o