79. Mechanizm wyładowania atmosferycznego

Wyładowanie atmosferyczne- wyładowanie elektryczne o charakterze iskrowym wewnątrz chmur, miedzy chmurami lub między chmurami a ziemią. W.a. powstaje na skutek rozdzielenia się naładowanych cząstek chmury burzowej, w pobliżu której natężenie pola elektrycznego wzrasta do wartości 500-1000 kV/m, co wywołuje jonizację lawinową gazu w chmurze. Wyładowanie piorunowe może mieć charakter liniowy, kulisty, paciorkowy lub łańcuchowy. W.a. przebiega w dwóch fazach. Wyładowanie wstępne ma postać wielokrotnych wyładowań urwanych, powtarzających się co ok. 25 μs. Gdy wyładowanie wstępne osiągnie powierzchnię ziemi, rozpoczyna się w.a. główne, podczas którego dochodzi do przepływu silnego prądu o natężeniu 10-200 kA. W.a. towarzyszą efekty świetlne- błyskawice i efekty akustyczne- grzmoty.

Do ochrony przed w.a. służą przewody odgromowe lub izolatory piorunochronowe.

80. Prawo Coulomba

Jest to podstawowe prawo elektrostatyki charakteryzujące oddziaływania między ładunkami punktowymi. Zgodnie z prawem Coulomba siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Prawo to można przedstawić za pomocą wzoru:

w którym:

F - siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych,

q₁ , q₂ - punktowe ładunki elektryczne,

r - odległość między ładunkami,

k - współczynnik proporcjonalności:

k=

gdzie:

ε₀- przenikalność elektryczna próżni

81.Pole elektrostatyczne, pole ładunku punktowego i dipola

Polem elektrostatycznym nazywamy właściwość przestrzeni, wewnątrz której działają siły elektrostatyczne.

P.e. jest polem wektorowym, którego źródłem jest nieruchomy ładunek elektryczny. Na ładunek elektryczny umieszczony w dowolnym punkcie pola działa siła pola. Każdemu punktowi p.e przypisujemy wektor natężenia pola (E) zdefiniowany jako stosunek siły działającej na ładunek punktowy q umieszczony w tym punkcie do jego wartości:

P.e. jest polem zachowawczym, tzn. że praca wykonana przez siły pola nie zależy od drogi, a tylko od początkowego i końcowego położenia ładunku. Rozróżniamy p.e. jednorodne, w którym natężenie pola jest stałe w każdym punkcie, i p.e. centralne, w którym siła zmienia się z odległością, jak w prawie Coulomba. P.e .jest szczególnym przypadkiem pola elektromagnetycznego.

Linie pola elektrostatycznego
Umożliwiają graficzne przedstawienie kierunku i wartości natężeń pola. Wektor natężeń pola w dowolnym punkcie jest styczny do lini pola przechodzącej przez ten punkt

Linie ładunku punktowego :




Pole jednorodne - linie pola są równoległe, a wartość natężenia jest stała.

Pole centralne - siły działają wzdłuż promienia.

Własności linii pola elektrostatycznego:

• nigdzie się nie przecinają;

• wychodzą z ładunku + a schodzą się w ładunku  - ;

• dla ładunków punktowych są to krzywe otwarte;

• są zawsze ^ do powierzchni;

• można je wystawić w każdym punkcie pola;

• im więcej linii, tym natężenie większe

Pole ładunku punktowego

Pole dipola

Dipol elektryczny składa się z dwóch cząstek o jednakowej wartości ładunku q, ale o przeciwnym znaku, znajdujących się w odległości d od siebie. Elektryczny moment dipolowy p dipola ma wartość qd i jest skierowany od ładunku ujemnego do dodatniego. Wartość natężenia pola wytworzonego przez dipol, w odległym punkcie na osi dipola (prostej przechodzącej przez oba ładunki) wynosi:

E=

Gdzie z- odległość między punktem i środkiem dipola, a p= qd

82. Pole elektrostatyczne naładowanej linii

Ciągłe rozkłady ładunków są to rozkłady składające się z bardzo wielu lezących blisko siebie ładunków punktowych, rozłożonych wzdłuż linii, na powierzchni, czy w pewnej objętości. Takie rozkłady mogą zawierać ogromna liczbę ładunków punktowych, dlatego też wytwarzane przez nie pola elektryczne znajdujemy, korzystając z zasad analizy matematycznej, a nie przez rozważanie poszczególnych ładunków punktowych.

Gdy mamy doczynienia z ciągłymi rozkładami ładunku, to wygodnie jest wyrazić ładunek za pomocą gęstości ładunku, a nie całkowitego ładunku:

- liniowa gęstość ładunku λ- ładunek na jednostkę długości linii [C/m], stosujemy dla naładowanej linii

- gęstość powierzchniowa σ [C/m²]

- gęstość objętościowa ρ [C/m³]

Pierścień naładowany jednorodnie- przykład z wykładów

Niech ds. będzie długością (wzdłuż łuku) elementu pierścienia. Ponieważ λ jest ładunkiem przypadającym na jednostkę długości, to taki element ma ładunek: dq= λds. Ten ładunek wytwarza natężenie pola E w punkcie P, który znajduje się w odległości r od elementu. Element ten traktujemy jak ładunek punktowy i po wielu przekształceniach otrzymujemy, że natężenie pola w tym punkcie wynosi:

83. Prawo Gaussa i zastosowania

Prawo Gaussa i prawo Coulomba chociaż mają różne postaci, są równoważnymi sposobami opisu związku między ładunkiem i natężeniem pola elektrycznego w sytuacjach statycznych.

Ma ono postać

:
, gdzie:

q wew- wypadkowy ładunek wewnątrz powierzchni Gaussa

Φ- wypadkowy strumień natężenia pola elektrycznego przez tę powierzchnie:

Zastosowania prawa Gaussa

Dla symetrycznych rozkładów ładunku możemy wyprowadzić wiele ważnych związków elektrostatycznych. Oto niektóre z nich:

1. Ładunek nadmiarowy na przewodniku znajduje się tylko na zewnętrznej jego powierzchni.

2. Natężenie pola elektrycznego przy zewnętrznej powierzchni naładowanego przewodnika jest prostopadłe do tej powierzchni i ma wartość:

(powierzchnia przewodnika)

σ- gęstość powierzchniowa ładunku

Wewnątrz przewodnika mamy E=0

3. Symetria cylindryczna. Natężenie pola elektrycznego nieskończonej lini naładowanej z gęstością liniową ładunku λ jest w dowolnym punkcie prostopadłe do naładowanej linii i ma wartość:

(naładowana linia)

Gdzie r- odległość punktu od naładowanej linii

4. Symetria płaszczyznowa. Natężenie pola elektrycznego nieskończonej nieprzewodzącej płyty, naładowanej jednorodnie z gęstością powierzchniową ładunku σ jest prostopadłe do płaszczyzny płyty i wynosi:

(naładowana płaszczyzna)

5. Powłoka sferyczna jednorodnie naładowana. Natężenie pola elektrycznego na zewnątrz sferycznej jednorodnie naładowanej powłoki o promieniu r i całkowitym ładunku q jest skierowana radialnie i ma wartość:

(powłoka sferyczna, dla r≥R)

Gdzie: r to odległość od środka powłoki do punktu, w którym wartość E jest wyznaczona (dla punktów na zewnątrz powłoki ładunek zachowuje się tak, jakby był skupiony w środku sfery). Natężenie pola wewnątrz sferycznej powłoki naładowanej jednorodnie jest równe zeru

E=0 (powłoka sferyczna, dla r<R).

6. Kula pełna (izolator). Natężenie pola elektrycznego wewnątrz jednorodnie naładowanej kuli jest skierowana radialnie i ma wartość:

84. Potencjał elektryczny, różnica potencjałów

Potencjał ładunku punktowego

W przypadku pola elektrycznego wytwarzanego przez punktowy ładunek elektryczny:

Zgodnie z definicją potencjału, gdzie W_∞ jest pracą siły elektrycznej wykonanej przy przeniesieniu ładunku daleko od ładunku wytwarzającego pole elektryczne. Zatem, ponieważ: W_∞= E_p- E_∞ , a energia potencjalna pola elektrycznego ładunku punktowego wyraża się wzorem:

Z czego wynika:

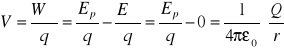
Jednostka: wolt

J/C= V

Potencjał elektryczny a natężenie pola elektrycznego

Potencjał elektryczny a praca w polu elektrycznym

Rozpatrując pole elektryczne rozważyć możemy jaka praca potrzebna jest aby przenieść (przemieścić) dany ładunek q z punktu P do punktu R rozważanego pola. Rozpatrzmy wpierw jednak przeniesienie danego ładunku z punktu P (lub R) do nieskończoności ; wówczas z definicji potencjału elektrycznego wynika, że praca ta dana jest jako:

W_∞=V_p*q (dla punktu P)

W_∞=V_R*q (dla punktu R)

Zatem praca potrzebna na przeniesienie ładunku q z punktu P do R dana jest jako:

W_PR=W_R∞-W_P∞= V_R*q -V_p*q= ∆V*q

Praca potrzebna na przeniesienie ładunku q z danego punktu P do innego punktu R zależy jedynie od:

• różnicy potencjałów między tymi punktami - zwanej inaczej napięciem elektrycznym,

• ładunku q.

Napięcie

Z potencjałem elektrycznym wiąże się pojęcie powierzchni ekwipotencjalnej

85. Natężenie pola elektrycznego

Natężenie pola elektrycznego E, jest to wielkość charakteryzująca pole elektryczne w dowolnym punkcie przestrzeni. N.p.e. definiujemy jako stosunek siły pola F działającej na umieszczony w tym punkcie ładunek próbne q₀, do wartości tego ładunku:

Kierunek natężenia E jest zgodny z kierunkiem siły działającej naładunek próbny (ładunek próbny jest zawsze dodatni!)

Aby zdefiniować pole elektryczne w pewnym obszarze należy podobnie zdefiniować natężenie we wszystkich punktach tego obszaru.

Ładunek punktowy

Aby znaleźć pole ładunku punktowego q w dowolnym punkcie, w odległości r od ładunku punktowego, umieszczamy w tym punkcie dodatni ładunek próbny.

Wartość siły elektrostatycznej działającej naładunek próbny (z prawa Coulomba):

a zatem wartość natężenia pola wynosi:

Dipol- patrz punkt 81

Naładowana linia- patrz punkt 82

86. Kondensatory: pojemność, połączenia równoległe oraz szeregowe, zastosowania

Pojemność kondensatora

Doprowadzenie napięcia do okładzin kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Jeżeli kondensator jako całość nie jest naelektryzowany, to cały ładunek zgromadzony na jego okładkach jest jednakowy, ale przeciwnego znaku. Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:

C=Q/U

• C - pojemność, w faradach

• Q - ładunek zgromadzony na jednej okładce, w kulombach

• U - napięcie elektryczne między okładkami, w woltach.

Pojemność wyrażana jest w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano-, mikro- i milifaradów.

Obliczanie pojemności

Pojemność kondensatora o określone konfiguracji obliczamy następująco:

1. Zakładamy, że na okładkach umieszczono ładunek q

2. Znajdujemy natężenie pola E wytworzonego przez ten ładunek

3. Obliczamy U

4. Wyznaczamy C ze wzoru ogólnego

Łączenie kondensatorów

Szeregowe

Równoległe

Zastosowania kondensatorów

87. Energia pola elektrycznego, energia pola magnetycznego

Elektryczna energia potencjalna- ładunek punktowy

Zmiana elektrycznej energii potencjalnej ładunku punktowego, przy jego przesunięciu z punktu początkowego do punktu końcowego w polu elektrycznym wynosi:

Gdzie W jest pracą wykonaną przez siłę elektrostatyczną(związaną z polem elektrycznym) nad ładunkiem punktowym, przy przesunięciu z punktu początkowego do końcowego. Jeśli energia potencjalna jest zdefiniowana tak, że jest równa zeru dla ładunku w nieskończoności, to elektryczna energia potencjalna ładunku punktowego w danym punkcie wnosi:

E_p= -W_∞,

Gdzie W_∞ jest pracą, wykonaną przez siłę elektrostatyczną nad ładunkiem punktowym, przy przesunięciu go z nieskończoności do rozważanego punktu.

Elektryczna energia potencjalna naładowanego kondensatora jest równa pracy, potrzebnej do jego naładowania. Energię te można powiązać z natężeniem pola elektrycznego w kondensatorze i wyciągnąć wniosek, że energia ta jest zmagazynowana w polu elektrycznym.

Energia dipola magnetycznego związana z jego ustawieniem

Magnetyczna energia potencjalna dipola magnetycznego, znajdującego się w polu magnetycznym jest równa:

Gdzie μ to dipolowy moment magnetyczne, a B to indukcja magnetyczna

Jeżeli dipol obraca się od pewnego początkowego ustawienia do ustawienia innego, to praca wykonana nad dipolem przez pole magnetyczne wynosi:

Energia magnetyczna zmagazynowana w cewce.

Jeżeli w cewce o indukcyjności L płynie prąd o natężeniu I, to w polu magnetycznym cewki zmagazynowana jest energia:

Jeżeli B oznacza wartość indukcji magnetycznej w dowolnym punkcie (wewnątrz cewki lub gdzie indziej), to gęstość zmagazynowanej energii jest w tym punkcie równa:

.

88. Prąd elektryczny: nośniki, natężenie, gęstość prądu

Prąd elektryczny- uporządkowany ruch ładunków elektrycznych w ośrodku.

Nośniki pradu elektrycznego- naładowane cząstki biorące udział w przewodnictwie elektrycznym substancji. Nośnikami p.e. w metalach są elektrony zwane elektronami przewodnictwa, w cieczach są to jony dodatnie i ujemne, w gazach zjonizowanych- elektrony i jony, w półprzewodnikach- elektrony i dziury (puste miejsca po elektronach). Rozróżniamy p.e. stały, którego natężenie nie ulega zmianie, i zmienny, gdy natężenie prądu ulega zmianie co do wartości i kierunku. Przepływ p.e. opisywany jest prawami prądu: Ohma i Kirchhoffa.

Natężenie prądu elektrycznego w przewodniku zdefiniowane jest wzorem:

Gdzie q jest ilością ładunku (dodatniego) przepływającego w czasie t przez powierzchnię przekroju poprzecznego przewodnika. Kierunek p.e. wybieramy umownie jako kierunek, w którym poruszałyby się dodatnie nośniki ładunku.

Jednostka- amper [C/s= A]

Gęstość prądu elektrycznego

Natężenie prądu elektrycznego (skalar) jest powiązane z gęstością prądu elektrycznego (wektor) wzorem:

Gdzie dS(wektor) jest wektorem prostopadłym do elementu powierzchni o polu dS. Wektor J ma taki sam kierunek jak prędkość poruszających się ładunków, jeśli są one dodatnie i przeciwny jeśli są ujemne

89. Prawa Kirchhoffa

Prawa Kirchhoffa - dwa prawa dotyczące obliczania natężeń i napięć stałego prądu elektrycznego w obwodach elektrycznych, sformułowane przez niemieckiego fizyka Gustava Kirchhoffa, żyjącego w XIX wieku.

Pierwsze prawo Kirchhoffa- prawo dotyczące przepływu prądu w rozgałęzieniach obwodu elektrycznego. Prawo to wynika z zasady zachowania ładunku. Wraz z drugim prawem Kirchhoffa umożliwia określenie przepływających prądów w obwodach elektrycznych.

Prawo to brzmi: Suma algebraiczna natężeń prądów dopływających(+) i odpływających(-) z danego węzła jest równa 0. lub Suma natężeń prądów dopływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

Z wykładów:

Drugie prawo Kirchhoffa dotyczy napięć w oczku: w zamkniętym obwodzie elektrycznym algebraiczna suma zmian potencjałów przy pełnym obejściu dowolnego oczka musi być równa zeru.

90,Rezystancja i rezystywność; prawo Ohma w obrazie makro- i mikroskopowym

Opór elektryczny, opór czynny, rezystancja, R- wielkość charakteryzująca przewodnik, której miarą jest stosunek napięcia elektrycznego U przyłożonego do końców przewodnika do natężenia prądu I płynącego przez przewodnik:

R= U/I

Jednostka- om [Ω= V/A]

Jeżeli wzór ten zapiszemy w postaci; I= U/R to widzimy, ze im większy jest opór przewodnika, tym mniejsze jest natężenie prądu.

Element obwodu, którego rolą jest zapewnienie określonego oporu- opornik.

Opór przewodnika zależy od sposobu, w jaki przyłożono do niego różnicę potencjałów.

Opór właściwy, rezystywność- wielkość charakteryzująca materiał z jakiego został wykonany przewodnik

Jednostka [Ω*m]

E= U/L

J= I/S

Opór elektryczny R	Opór właściwy ρ
Właściwość ciała	Właściwość materiału
Pod uwagę bierzemy różnicę potencjałów U oraz natężenie prądu I płynącego przez przewodnik	Pod uwagę bierzemy natężenie pola elektrycznego E oraz gęstość prądu J w rozważanym punkcie
Zależy od sposobu w jaki przyłożono napięcie U	Zależy od temperatury
R= U/I [Ω]	Ρ= E/J [Ωm]

Przewodność elektryczna właściwa (konduktywność) σ materiału- jest to odwrotność jego oporu właściwego

σ= 1/ρ

Jednostka: simens [S= 1/ Ωm]

Prawo Ohma

Inne istotne pojęcia związane z prądem

Półprzewodniki- materiały z małą liczba elektronów przewodnictwa, ale mogą stać się przewodnikami, gdy są „domieszkowane” innymi atomami, które dostarczają wolnych elektronów.

Nadprzewodniki- materiały, dla których opór elektryczny zanika przy niskich temperaturach.

91. Moc w obwodach elektrycznych

Moc P, czyli ilość energii przenoszonej w jednostce czasu, w danm przewodniku, na którym utrzymuje się przyłożona różnica potencjałów U, wynosi:

Wzór ten stosuje się do dowolnych przekazów energii elektrycznej

---