3. Kombinatoryka, zliczanie i generowanie obiektów kombinatorycznych, tożsamości kombinatoryczne, zasada włączania -wyłączania, podziały zbioru, liczby Stirlinga drugiego i pierwszego rodzaju.
Kombinatoryka pierwotnie elementarny dział teorii mnogości, którego przedmiotem było badanie różnych możliwych zestawień i ugrupowań, jakie można tworzyć z elementów dowolnego zbioru skończonego, np. zbioru liczb, liter, przedmiotów itp.; obecnie bardzo rozbudowana dyscyplina matematyczna badająca własności zbiorów skończonych; znajduje zastosowanie m.in. w teorii liczb, rachunku prawdopodobieństwa i informatyce. Stanowi jeden z działów matematyki dyskretnej.
Kombinatoryka zajmuje się zagadnieniami
przeliczenia (określenia liczby elementów),
wyliczenia (wypisania wszystkich elementów),
optymalizacji
zbiorów skończonych.
Kombinatoryka posługuje się terminologią nie występującą w innych działach matematyki, stąd pozorna jej odrębność. Najważniejszym jej zadaniem jest konstruowanie spełniających pewne określone warunki odwzorowań jednego zbioru skończonego w drugi oraz znajdowanie wzorów na liczbę tych odwzorowań.
Zliczanie obiektów kombinatorycznych - funkcje i rozmieszczenia
Klasycznym problemem kombinatorycznym jest zadanie sformułowane następująco:
Dane są dwa zbiory skończone X i Y, przy czym ![]()
i ![]()
. Ile jest funkcji f: X→Y spełniających dane ograniczenia?
Inaczej problem ten można sformułować następująco:
na ile sposobów można rozmieścić n obiektów (zbiór X - zbiór obiektów) w m pudełkach (zbiór Y - zbiór pudełek), y=f(x) określa numer pudełka dla obiektu x, albo
na ile sposobów można pokolorować n obiektów (zbiór X - zbiór obiektów) m kolorami (zbiór Y - zbiór kolorów), y=f(x) określa kolor dla obiektu x.
Można przyjąć, że każdą funkcję f: X→Y, gdzie X={1,2,…,n} i Y={1,2,…,m} określamy jako ciąg wartości funkcji <f(1),f(2),…,f(n)>, co zapisujemy <y1,y2,…,yn>.
Problem ten jest najprostszy jeżeli na rozmieszczenia nie nakładamy żadnych ograniczeń, ponieważ można udowodnić następujące twierdzenie:
Twierdzenie 1
Jeżeli ![]()
i ![]()
, to liczba wszystkich funkcji f: X→Y jest równa mn.
Dowód
Przyjmując X={1,2,…,n} pytamy ile jest wszystkich ciągów <y1,y2,…,yn> o wyrazach ze zbioru m elementowego Y.
Każdy wyraz możemy zapisać na m sposobów, co daje nam mm…m (n razy), czyli mn.
Jeżeli ustalimy ograniczenie, że każde pudełko zawiera co najwyżej jeden obiekt to takie rozmieszczenia odpowiadają funkcjom różnowartościowym. Liczbę wszystkich funkcji różnowartościowych ze zbioru n-elementowego do zbioru m-elementowego oznaczamy przez [m]n.
Twierdzenie 2
Jeżeli ![]()
, ![]()
i nm to liczba wszystkich funkcji różnowartościowych f: X→Y jest równa
[m]n=m(m-1)(m-2)…(m-n+1),
przyjmujemy, że [m]0=1.
Dowód
Przyjmując X={1,2,…,n} i nm, pytamy ile jest wszystkich różnowartościowych ciągów <y1,y2,…,yn> o wyrazach ze zbioru m elementowego Y. Wyraz y1 możemy zapisać na m sposobów, wyraz y2 już tylko na m-1 sposobów, wyraz y3 na m-2 sposoby itd. aż do wyrazu yn który zapisuje się na m-(n-1) sposobów, co daje liczbę m(m-1)(m-2)…(m-n+1), czyli liczba wszystkich funkcji różnowartościowych wynosi [m]n=m(m-1)(m-2)…(m-n+1).
Jeżeli n>m to [m]n=0 i nie istnieje funkcja różnowartościowa
f: X→Y.
Jeżeli n=m, to każda funkcja różnowartościowa f: X→Y jest wzajemnie jednoznacznym odwzorowaniem zbioru X na zbiór Y, czyli jest bijekcją.
Twierdzenie 3
Jeżeli ![]()
i ![]()
, to liczba wszystkich bijekcji f: X Y jest równa
[n]n=n(n-1)(n-2)…1 co oznaczamy przez n! (n silnia).
Dowód
Przyjmując ![]()
i ![]()
i podstawiając zamiast m, n do wzoru [m]n=m(m-1)(m-2)…(m-n+1) otrzymujemy
[n]n=n(n-1)(n-2)…1.
Jeżeli rozmieszczamy n obiektów w m pudełkach, przy czym każde pudełko zawiera ciąg (a nie jak poprzednio zbiór) obiektów, przy czym dwa rozmieszczenia uważa się za równe jeśli każde pudełko zawiera taki sam ciąg obiektów. Rozmieszczenia tego typu nazywa się rozmieszczeniami uporządkowanymi n obiektów w m pudełkach ich liczbę oznaczamy przez [m]n.
Twierdzenie 4
Liczba rozmieszczeń uporządkowanych n obiektów w m pudełkach wynosi
[m]n=m(m+1)…(m+n-1),
przyjmujemy, że [m]0=1.
Dowód
Konstruujemy rozmieszczenie uporządkowane przez kolejne dodawanie nowych obiektów. Pierwszy obiekt możemy rozmieścić na m sposobów, drugi na m+1 sposobów, gdyż można go umieścić w jednym z m-1 pustych pudełek lub w pudełku zawierającym pierwszy obiekt przed lub za tym obiektem. Ogólnie jeżeli zostało już rozmieszczone i-1 obiektów, przy czym dla k=1,2,…,m w k-tym pudełku znajduje się rk obiektów, wtedy i-ty obiekt możemy dodać na rk+1 sposobów do k-tego pudełka, co daje w sumie
(r1+1)+(r2+1)+…+(rm+1)=(r1+r2+…+rm)+m=i-1+m=m+i-1
możliwości. Wszystkich rozmieszczeń uporządkowanych jest więc [m]n=m(m+1)…(m+n-1).
Przykład
Rozmieścić dwa obiekty a, b w trzech pudełkach
Pudełko 1 |
Pudełko 2 |
Pudełko 3 |
a |
b |
|
a |
|
b |
b |
a |
|
b |
|
a |
|
a |
b |
|
b |
a |
ab |
|
|
ba |
|
|
|
ab |
|
|
ba |
|
|
|
ab |
|
|
ba |
[3]2=34=12.
Obiekty kombinatoryczne
Permutacje
Permutacją zbioru n-elementowego X nazywamy dowolną wzajemnie jednoznaczną funkcję f:X→X. Inaczej permutacją zbioru
n-elementowego X nazywamy dowolny różnowartościowy ciąg długości n o elementach ze zbioru X. Jeżeli upraszczając przyjmiemy, że X={1,2,…,n} to dowolną permutację f:X→X utożsamiać można z ciągiem <a1,a2,…,an>, gdzie ai=f(i) dla i=1,2,…,n. Zbiór wszystkich permutacji tego zbioru oznaczamy przez Pn.
Na mocy twierdzenia 3 liczba wszystkich permutacji zbioru
n-elementowego X wynosi n!, czyli 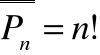
.
Permutację zbioru n-elementowego X f:X→X, gdzie i=f(i) nazywamy permutacją identycznościową.
Kombinacje
Weźmy teraz pod uwagę skończony n-elementowy zbiór A,
każdy k-elementowy podzbiór zbioru A nazywamy k-elementową kombinacją bez powtórzeń zbioru n-elementowego, należy zauważyć, że kn. Liczbę wszystkich k-elementowych podzbiorów zbioru A oznaczamy przez 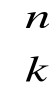
(n po k) i nazywamy współczynnikiem dwumiennym (współczynnikiem dwumianowym Newtona, symbolem Newtona).
Twierdzenie 5
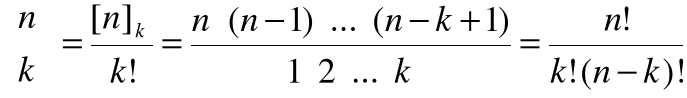
Dowód
Każdy z [n]k ciągów różnowartościowych długości k wyznacza podzbiór k-elementowy złożony z elementów występujących w tym ciągu, przy czym ten sam podzbiór A otrzymujemy z dokładnie k! ciągów, odpowiadających wszystkim permutacjom zbioru A.
Stąd 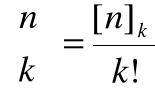
, korzystając teraz z twierdzenia 2 otrzymujemy
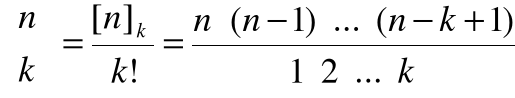
,
co przy zastosowaniu symbolu silni można zapisać w postaci
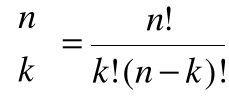
.
Dla skończonego n-elementowy zbióru A, można określić
k-elementowy podzbiór z powtórzeniami zbioru A, który nazywamy k-elementową kombinacją z powtórzeniami zbioru n-elementowego. Liczba wszystkich k-elementowych kombinacji z powtórzeniami zbioru n-elementowego A jest równa liczbie ciągów niemalejących długości k o elementach ze zbioru {1,2,…,n}, wynika to stąd, że elementy każdego podzbioru można jednoznacznie ustawić w ciąg niemalejący. Oznacza to, że liczba wszystkich k-elementowych kombinacji z powtórzeniami zbioru n-elementowego A wynosi
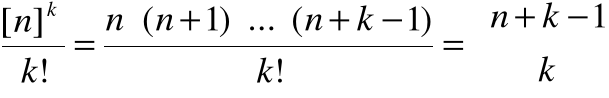
.
Wariacje
Każdy k-wyrazowy ciąg elementów n-elementowego zbioru A nazywamy k-elementową wariacją z powtórzeniami zbioru
n-elementowego. Na mocy twierdzenia 1 mamy, że liczba wszystkich k-wyrazowych wariacji z powtórzeniami zbioru
n-elementowego wynosi nk.
Każdy k-wyrazowy ciąg różnych elementów n-elementowego zbioru A nazywamy k-elementową wariacją bez powtórzeń zbioru
n-elementowego. Na mocy twierdzenia 2 mamy, że liczba wszystkich k-wyrazowych wariacji bez powtórzeń zbioru n-elementowego wynosi [n]k=n(n-1)…(n-k+1).
Tożsamości kombinatoryczne
[m]n=(m-n+1)[m]n-1
[m]n=
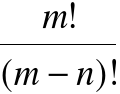
[m]n=[m+n-1]n
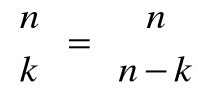
symetria symbolu Newtona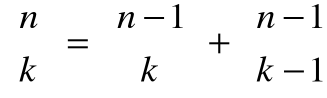
trójkąt Pascala
Tożsamości kombinatoryczne
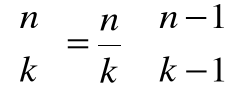
pochłanianie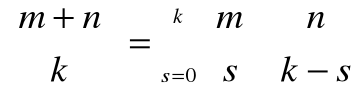
tożsamość Cauchy'ego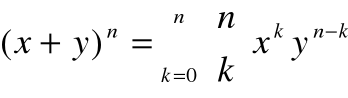
, dla x, yR i nN.
Ponieważ liczba wszystkich podzbiorów zbioru n-elementowego A wynosi 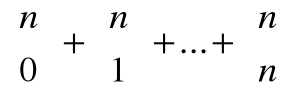
, korzystając teraz ze wzoru dwumianowego mamy
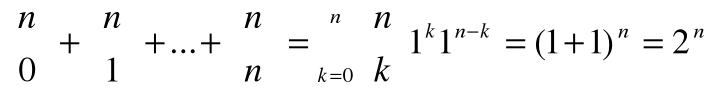
,
czyli wyprowadziliśmy wzór na moc zbioru potęgowego P(A) skończonego n-elementowego zbioru A. Czyli 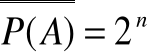
.
Zasada włączania -wyłączania
Zasada włączania - wyłączania pozwala znaleźć liczbę elementów zbioru A1A2…An, gdzie Ai (dla i=1,2,…,n) są zbiorami skończonymi. Sumę taką nazywamy sumą uogólnioną zbiorów Ai i oznaczamy przez 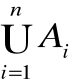
.
Proste przypadki zasady włączania i wyłączania:
Twierdzenie 6
Jeżeli n=2 to 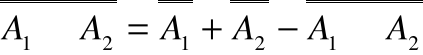
.
Dowód
Jeżeli 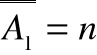
oraz 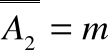
i A1A2=, czyli 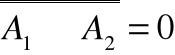
to liczba elementów zbioru A1A2 wynosi 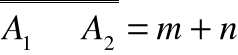
-0 czyli 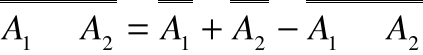
.
Jeżeli 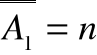
oraz 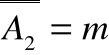
i A1A2 oraz 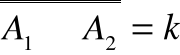
to elementy wspólne liczone są w sumie 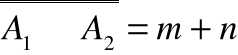
podwójnie i należy je odjąć czyli 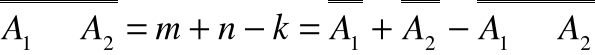
.
Twierdzenie 7
Jeżeli n=3 to
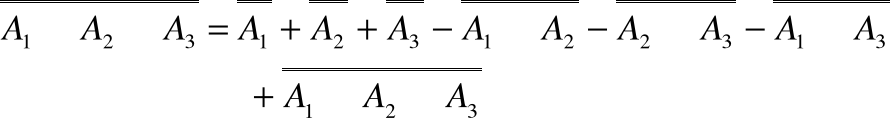
Dowód
Wykorzystując twierdzenie 1 i prawo rozdzielności sumy i iloczynu zbiorów mamy:
A1A2A3=(A1A2)A3 co daje na mocy twierdzenia 1
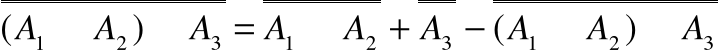
oraz 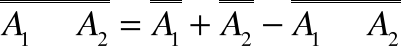
i
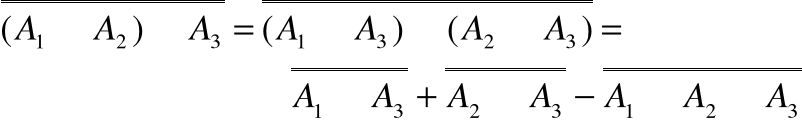
co daje wzór
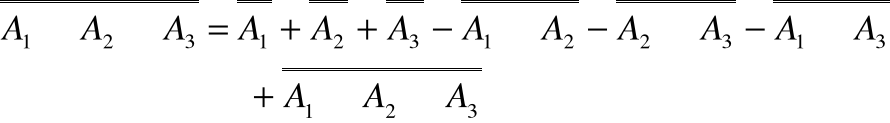
Uogólniając dla n można sformułować zasadę włączania - wyłączania następująco:
Zasada włączania-wyłączania
Aby wyznaczyć liczbę elementów zbioru 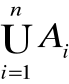
należy dodać do siebie liczności poszczególnych zbiorów Ai (włączanie), odjąć liczności wszystkich iloczynów zbiorów AiAj (wyłączanie), dodać liczności wszystkich iloczynów trzech zbiorów AiAjAk (włączanie), odjąć liczności wszystkich iloczynów czterech zbiorów AiAjAkAl., itd.
Oznacza to że dodajemy liczności iloczynów nieparzystej liczby zbiorów a odejmujemy liczności iloczynów parzystej liczby zbiorów.
Można to zapisać następująco:
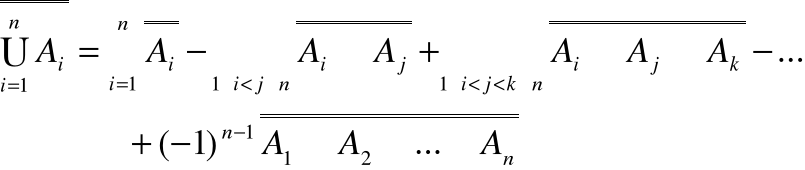
Podziały (rozkłady) zbioru
Podziałem (rozkładem) zbioru n - elementowego X na k bloków nazywamy dowolną rodzinę ={B1, B2,…, Bk} taką, że
Bi , dla 1ik,
B1B2…Bk = X,
BiBj=.
Podzbiory B1, B2,…, Bk zbioru X nazywamy blokami podziału .
Zbiór wszystkich podziałów zbioru X na k bloków oznacza się k(X), natomiast zbiór wszystkich podziałów przez (X). Zachodzą następujące własności:
(X)=1(X)2(X)…k(X) oraz
zbiór {1(X), 2(X),…, k(X)} jest podziałem zbioru (X).
Liczby Stirlinga drugiego rodzaju i pierwszego rodzaju
Liczbą Stirlinga drugiego rodzaju S(n,k) nazywamy liczbę podziałów zbioru n - elementowego na k bloków:
S(n,k)=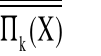
, gdzie ![]()
=n.
Przyjmujemy, że S(0,0)=1, gdyż pusta rodzina bloków jest podziałem zbioru pustego.
Przykład
Dla zbioru 4-elementowego X={1,2,3,4} mamy S(4,2)=7, ponieważ istnieją tylko następujące podziały zbioru X:
{{1,2,3}, {4}}, {{1,2,4}, {3}}, {{1,3,4}, {2}}, {{2,3,4}, {1}}, {{1,2}, {3,4}}, {{1,3}, {2,4}}, {{1,4}, {2,3}}.
Własności liczb Stirlinga drugiego rodzaju:
S(n,k)=0 dla k>n,
S(n, n) =1 dla n≥0,
S(n,0)=0 dla n>0,
S(n,1)=1 dla n>0,
S(n,k)=S(n-1,k-1)+kS(n-1,k) dla 0<k<n,
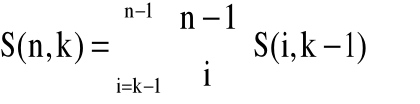
, dla k>1,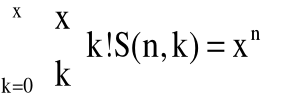
, dla n≥0,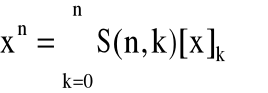
, dla n≥0.
Liczby Stirlinga drugiego rodzaju S(n,k)
n\k |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
7 |
6 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
15 |
25 |
10 |
1 |
0 |
0 |
0 |
0 |
0 |
6 |
31 |
90 |
65 |
15 |
1 |
0 |
0 |
0 |
0 |
7 |
63 |
301 |
350 |
140 |
21 |
1 |
0 |
0 |
0 |
8 |
127 |
966 |
1701 |
1050 |
266 |
28 |
1 |
0 |
0 |
9 |
255 |
3025 |
7770 |
6951 |
2646 |
462 |
36 |
1 |
0 |
10 |
511 |
9330 |
34105 |
42525 |
22827 |
5880 |
750 |
45 |
1 |
Liczbami Stirlinga pierwszego rodzaju s(n,k) nazywamy współczynniki przy kolejnych k-potęgach zmiennej x w wielomianie [x]n, czyli
[x]n=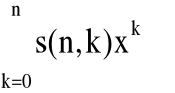
.
Przyjmujemy, że s(0,0)=1.
Własności liczb Stirlinga pierwszego rodzaju:
s(n,k)=0 dla k>n,
s(n, n) =1 dla n≥0,
s(n,0)=0 dla n>0,
s(n,k)=s(n-1,k-1)-(n-1)s(n-1,k) dla 0<k<n.
Liczby Stirlinga pierwszego rodzaju s(n,k)
n\k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
2 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
2 |
-3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
-6 |
11 |
-6 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
24 |
-50 |
35 |
-10 |
1 |
0 |
0 |
0 |
0 |
0 |
6 |
-120 |
274 |
-225 |
85 |
-15 |
1 |
0 |
0 |
0 |
0 |
7 |
720 |
-1764 |
1624 |
-735 |
175 |
-21 |
1 |
0 |
0 |
0 |
8 |
-5040 |
13068 |
-13132 |
6769 |
-1960 |
322 |
-28 |
1 |
0 |
0 |
9 |
40320 |
-109584 |
118124 |
-67284 |
22449 |
-4536 |
546 |
-36 |
1 |
0 |
10 |
-362880 |
1026576 |
-1172700 |
723680 |
-269325 |
63273 |
-9450 |
870 |
-45 |
1 |
1-1
na
Wyszukiwarka
Podobne podstrony:
matdyskr5, 2 Semestr, Matematyka dyskretna, MDwyklady
pytegzmatdyskr2009wi, 2 Semestr, Matematyka dyskretna, matematyka dyskretna 2009, egzamin pytania i
md-2009, 2 Semestr, Matematyka dyskretna, matematyka dyskretna 2009, egzamin pytania i odpowiedzi
fibb, Chomiczek, Studia, Semestr 2, Matematyka Dyskretna, Matematyka dyskretna
Matematyka dyskretna md wyklad 3
ListazadanMD1, 2 Semestr, Matematyka dyskretna, MDzadania
ListazadanMD4, 2 Semestr, Matematyka dyskretna, MDzadania
ListazadanMD67, 2 Semestr, Matematyka dyskretna, MDzadania
Matematyka dyskretna, md wyklad 2
Matematyka dyskretna, md wyklad 2b
pytania na egz md, semestr 2, matematyka dyskretna II
odp to 29, Informatyka SGGW, Semestr 2, Matematyka dyskretna 2, dysk
tabelku do kolok A, Studia Informatyka 2011, Semestr 2, Matematyka dyskretna, labolatoria Dmytryszyn
dyskretna2, Studia, PWR, 2 semestr, Matematyka dyskretna
pytegzMatDyskr2010ZSB, 2 Semestr, Matematyka dyskretna, MDwyklady
więcej podobnych podstron