WOJSKOWA AKADEMIA TECHNICZNA

Wydział Inżynierii Lądowej i Geodezji

RACHUNEK WYRÓWNAWCZY

Sprawozdanie z ćwiczenia

WYRÓWNANIE SIECI NIWELACYJNEJ

Sieć nr 33.

wykonali:

prowadzący: Kozioł Krzysztof G8X4S1

dr inż. Krzysztof Kroszczyński Kozikowski Marcin G8X4S1

1. Wstęp teoretyczny

1.1. Sieć niwelacyjna

Definicja niwelacji

Pomiary wysokości punktów budowli, elementów uzbrojenia terenu, reperów, jak również charakterystycznych punktów ukształtowania terenu ponad poziomem morza, są nazywane niwelacją. Umownym poziomem odniesienia dla Polski jest średni poziom Morza Bałtyckiego w Kronsztadzie (Zatoka Fińska). Pomiary wysokościowe są przeprowadzane za pomocą niwelatorów, natomiast jednoczesne pomiary sytuacyjne i wysokościowe za pomocą tachimetrów i odbiorników GPS.

Siecią niwelacyjną nazywamy zbiór punktów geodezyjnych, (wśród których jest przynajmniej jeden punkt o znanej wysokości), w którym dla wyznaczenia wysokości p punktów wykorzystano więcej niż p ciągów niwelacyjnych charakteryzujących wzajemne położenie wysokościowe tych punktów.

W celu wyrównania sieci niwelacyjnej wykonujemy następujące czynności:

• Obliczenie różnic przewyższeń z kierunku głównego i powrotnego

• Obliczenie błędu średniego podwójnej niwelacji ciągu 1 km oraz błędów średnich ciągów niwelacyjnych

• Przyjęcie modelu stochastycznego

• Ułożenie równań poprawek i zapisanie ich w postaci macierzowej

• Rozwiązanie układu równań normalnych

• Sprawdzenie poprawności obliczeń i zastosowanego modelu2. Dane wejściowe

(Skopiować ze zbioru /dane/ niwelacja_numersieci.txt)

lp j k dh_g dh_p d

1 2 1 2.628 2.623 0.39

2 3 2 -2.589 -2.584 0.53

3 4 1 2.320 2.315 0.32

4 1 5 -1.133 -1.136 0.58

5 5 2 -1.497 -1.494 0.37

6 3 5 -1.089 -1.086 0.43

7 6 3 1.501 1.506 0.34

8 5 4 -1.186 -1.182 0.35

9 6 5 0.409 0.414 0.34

10 7 4 -2.502 -2.507 0.41

11 5 7 1.314 1.315 0.72

12 8 5 -0.031 -0.028 0.56

13 5 9 -0.893 -0.888 0.57

14 9 6 0.483 0.478 0.45

15 8 7 1.282 1.283 0.39

16 9 8 0.923 0.918 0.47

17 9 3 1.982 1.977 0.79

18 7 1 -0.183 -0.189 0.57

19 10 1 2.319 2.324 0.43

20 11 10 -1.187 -1.184 0.45

21 1 11 -1.133 -1.137 0.72

22 11 2 -1.497 -1.492 0.38

23 3 11 -1.088 -1.094 0.53

24 12 11 0.409 0.405 0.44

25 12 3 1.501 1.498 0.36

lp x y ps

1 783.540 195.010 0

2 940.980 551.390 0

3 916.490 1084.530 0

4 556.120 414.540 0

5 633.090 759.520 0

6 573.610 1095.940 1

7 213.250 180.760 1

8 115.280 554.240 0

9 125.780 1024.660 0

10 1210.380 260.580 1

11 1287.350 702.490 0

12 1269.860 1144.400 0

numery punktów dowiązania

6 7 10

wysokości punktów dowiązania

98.454 100.186 97.679

macierz błędu punktów dowiązania

1.520 -0.816 0.017

-0.816 1.889 0.035

0.017 0.035 2.128

lp - liczba porządkowa

j, k - wskaźniki początku i końca niwelowanego odcinka (numery punktów)

dh_p - przewyższenie w przód w [m] - metrach

dh_w - przewyższenie w wstecz w [m] - metrach

d - długość ciągu w [km] - kilometrach

x,y - współrzędne punktów sieci w metrach - [m]

ps = 1 - punkt stały, ps = 0 - punkt wyznaczany

3. Szkic i opis elementów sieci

Szkic wykonujemy na podstawie tabeli (współrzędnych reperów) danych wejściowych

Rys. 1. Szkic sieci niwelacyjnej.

4. Wyznaczenie błędu średniego podwójnej niwelacji ciągu o długości 1 km

Ciągi są mierzone (tabela danych) w kierunku głównym, zaznaczono je strzałką na szkicu, oraz powrotnym. Przewyższenia niwelacyjne z kierunku głównego hg i powrotnego hp są uśredniane (z kierunku powrotnego zapisano je z odwrotnym znakiem):

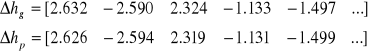
(1)

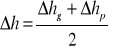
. (2)

Błąd średni
podwójnej niwelacji ciągu o długości 1 km wyznaczamy na podstawie różnic przewyższeń z kierunków głównego i powrotnego wykorzystując zależność:

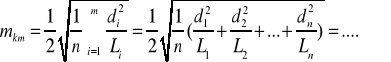
(3)

gdzie n to ilość ciągów niwelacyjnych,
długość ciągu niwelacyjnego (w km), d to wektor różnic:

(4)

wyrażamy w mm (różnice nie powinny przekraczać wartości dopuszczalnych, zależnych od klasy niwelacji). Mnożnik
wynika z faktu, że jednostkami przewyższeń są metry [m].

Korzystając z zależności (3) otrzymano

Wartość
wyrażono w milimetrach.

5. Wyniki wyrównania

	Pomiary	Błędy pomiarów	Wyrównane pomiary	Błędy wyrównanych pomiarów	Poprawki	Błędy poprawek	Test poprawek
Lp.	(przew. [m])	bl. przew [mm]	przew.popr [m]	bl.przew.popr [mm]	pop. v	3*mv	test
1	2.6255	2	2.628	1	2.	5.	+
2	- 2.5865	2	- 2.585	1	2.	6.	+
3	2.3175	2	2.317	1	-0.	4.	+
4	- 1.1345	2	- 1.132	1	2.	7.	+
5	- 1.4955	2	- 1.496	1	-0.	5.	+
6	- 1.0875	2	- 1.089	1	-2.	5.	+
7	1.5035	2	1.503	1	-1.	5.	+
8	- 1.184	2	- 1.185	1	-1.	4.	+
9	0.4115	2	0.414	1	2.	5.	+
10	- 2.5045	2	- 2.503	1	1.	5.	+
11	1.3145	3	1.318	1	4.	8.	+
12	- 0.0295	2	- 0.032	1	-3.	6.	+
13	- 0.8905	2	- 0.891	1	-0.	6.	+
14	0.4805	2	0.477	1	-3.	5.	+
15	1.2825	2	1.286	1	4.	4.	+
16	0.9205	2	0.923	2	2.	5.	+
17	1.9795	3	1.980	2	1.	7.	+
18	- 0.186	2	- 0.186	1	-0.	7.	+
19	2.3215	2	2.321	1	-1.	6.	+
20	- 1.1855	2	- 1.186	1	-1.	5.	+
21	- 1.135	3	- 1.135	1	0.	7.	+
22	- 1.4945	2	- 1.493	1	1.	5.	+
23	- 1.091	2	- 1.091	1	-0.	6.	+
24	0.407	2	0.408	2	1.	4.	+
25	1.4995	2	1.499	2	-0.	4.	+

Tab. 2. Wyniki wyrównania sieci niwelacyjnej.

Nr.pkt	wys. [m]	bl.wys [mm]	X [m]	Y [m]
1	100.000	1	783.54	195.01
2	97.372	1	940.98	551.39
3	99.957	1	916.49	1084.53
4	97.683	1	556.12	414.54
5	98.868	1	633.09	759.52
6	98.454	0	573.61	1095.94
7	100.186	0	213.25	180.76
8	98.900	1	115.28	554.24
9	97.977	1	125.78	1024.66
10	97.679	0	1210.38	260.58
11	98.865	1	1287.35	702.49
12	98.458	2	1269.86	1144.40

Tab. 3. Wyznaczone wysokości reperów sieci niwelacyjnej.

5.1. Parametry testów statystycznych

Parametr m0 pierwszego etapu wyrównania: m0 = 1.00

Test
: chi = 16.0 chi2 = 26.3, chi < chi2.

Wnioski

Na podstawie przeprowadzonych obliczeń można stwierdzić, że:

Wartości błędów wysokości punktów (reperów) sieci nie przekraczają 2 mm. Jest to wynik zadowalający, sugerujący iż przeprowadzona procedura wyrównania została wykonana w sposób jak najbardziej poprawny. Wyrównanie przeprowadziliśmy w jednym etapie, gdyż po pierwszym, wstępnym wyrównaniu błąd średni zawarł się w dopuszczalnym zakresie, co sugerowało iż przyjęty przez nas model stochastyczny oddaje wiernie rzeczywistośc i nie należy dokonywac jego korekty.

Błędy pomiarów wyrównanych są mniejsze od błędów obserwacji co jest jak najbardziej właściwa sytuacja. Zarówno test globalny jak i lokalny dają wyniki pozytywne.

Warszawa 9.03.2010 r.

2

---