POLITECHNIKA CZĘSTOCHOWSKA
KATEDRA FIZYKI
ĆWICZENIE nr 14
Pomiar promieni krzywizny soczewki płasko-wypukłej metodą pierścieni Newtona
Wykonał:
Sebastian Ciupa
Wydział Elektryczny
grupa III
1. Wprowadzenie
Zjawisko interferencji światła występuje wtedy, gdy w określonym punkcie przestrzeni nakładają się dwie jednakowe, monochromatyczne fale świetlne ( czyli fale o jednakowej częstotliwości ) zwane falami spójnymi (koherentnymi). Wynik interferencji zależy od różnicy faz spotykających się fal. Koherentne wiązki światła zachowują niezmienną w czasie różnicę faz. Światło pochodzące z dwu różnych źródeł nie spełnia tego warunku. Aby uzyskać dwie wiązki koherentne kierujemy światło wychodzące z punktowego źródła światła na dwie wąskie równoległe szczeliny. Wynik interferencji zależny jest od różnicy faz spotykających się fal. Różnica faz może powstać jedynie z powodu różnicy dróg jakie przebywają fale do punktu, w którym nastąpi interferencja.
Jeśli ta różnica dróg:
S = nλ
czyli jeśli równa jest całkowitej wielokrotności długości fali, wówczas w miejscu spotkania mamy wzmocnienie drgań.
Jeśli różnica dróg:
S = (2n+1)λ/2
tzn. równa się nieparzystej wielokrotności λ/2, drgania znoszą się, następuje częściowe lub całkowite wygaszenie fal ( w zależności od amplitudy drgań).
Jednym z przykładów interferencji fal świetlnych jest powstawanie tzw. pierścieni Newtona.
Otrzymujemy je za pomocą dwóch płytek szklanych bardzo dokładnie oszlifowanych: płaskiej i wypukłej (rys. 1).
I
II
Między tymi płytkami znajduje się cienka warstewka powietrza, której grubość wzrasta stopniowo od środka płytek ku brzegom. Gdy układ ten oświetlimy światłem jednobarwnym padającym normalnie, to w świetle odbitym ujrzymy wielką liczbę współśrodkowych pierścieni, na przemian jasnych i ciemnych, ośrodku ciemnym w miejscu zetknięcia się obu powierzchni. Pierścienie te powstają jako wynik interferencji promieni odbitych od powierzchni sferycznej I i powierzchni płaskiej II. W przypadku powstawania pierścienia ciemnego różnica dróg takich dwóch promieni musi wynosić:
(2n + 1)λ/2
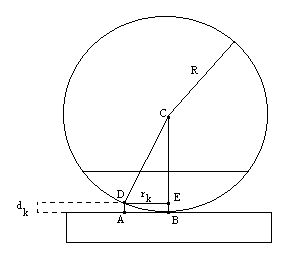
Załóżmy, że w punkcie B powstaje k- ty pierścień ciemny. W punkcie A powstaje również pierścień ciemny - zmiana fazy (gdyż następuje odbicie fali od środowiska optycznie gęstszego, czemu towarzyszy zmiana fazy o 180°; ta zmiana fazy odpowiada różnicy czasu, równej połowie okresu lub różnicy dróg, równej połowie długości fali). Różnica dróg dla k- tego krążka wynosi
S= 2e + λ/2
Z warunku powstawania prążka ciemnego mamy:
![]()
Z trójkąta prostokątnego ADC mamy:
![]()
Skąd
![]()
Z trójkąta DCE znajdziemy, że
![]()
Gdzie R jest promieniem krzywizny powierzchni I.
Ponieważ dk<<rk można przyjąć:
![]()
![]()
Uwzględniając wzór powyższy otrzymujemy zależność następującą:
Ze wzoru tego wynika, że znając długość fali światła oświetlającego układ, przez pomiar k- tego prążka można znaleźć promień krzywizny soczewki lub na odwrót. Aby uniknąć błędu spowodowanego niedokładnym oznaczeniem środka pierścienia ciemnego mierzymy średnice dwóch ciemnych pierścieni ( możliwie daleko odległych od siebie ) np. m- tego i n- tego.
![]()
![]()
Wówczas
![]()
Odejmując stronami te równania otrzymamy:
2. Układ pomiarowy
W celu wykonania ćwiczenia posługujemy się mikroskopem i układem płytek. Światło z lampy sodowej jest skupiane za pomocą soczewki. Po odbiciu od zwierciadła (wewnątrz mikroskopu) pada na układ płytek, dających wskutek odbicia i interferencji pierścienie Newtona. Promienie odbite trafiają do obiektywu mikroskopu, a następnie do oka obserwatora. W okularze mikroskopu znajduje się nić pajęcza, którą możemy przesuwać za pomocą śrub mikrometrycznych.
3. Tabela pomiarowa
Numer pierścienia K |
Wskazania mikrometru na lewo l na prawo p [m] [ m] |
rk= [m] |
m,n
|
λ [m] |
R [m] |
Rśr [m] |
|
|
29.84*10-3 |
21.85*10-3 |
3.99*10-3 |
35,15 |
5.89*10-7 |
4.24 |
|
|
30.13*10-3 |
21.56*10-3 |
4.28*10-3 |
20,7 |
5.89*10-7 |
4.28 |
|
|
30.43*10-3 |
21.26*10-3 |
4.58*10-3 |
30,9 |
5.89*10-7 |
4.28 |
|
|
30.68*10-3 |
21.00*10-3 |
4.84*10-3 |
20,6 |
5.89*10-7 |
4.27 |
|
|
30.90*10-3 |
20.75*10-3 |
5.07*10-3 |
25,15 |
5.89*10-7 |
4.30 |
|
|
31.93*10-3 |
19.57*10-3 |
6.18*10-3 |
30,25 |
5.89*10-7 |
4.35 |
|
|
32.90*10-3 |
18.60*10-3 |
7.15*10-3 |
25,9 |
5.89*10-7 |
4.25 |
|
|
33.75*10-3 |
17.80*10-3 |
7.97*10-3 |
30,20 |
5.89*10-7 |
4.29 |
|
|
34.51*10-3 |
17.03*10-3 |
8.74*10-3 |
35,10 |
5.89*10-7 |
4.24 |
|
|
35.16*10-3 |
16.37*10-3 |
9.39*10-3 |
25,10 |
5.89*10-7 |
4.28 |
|
|
35.64*10-3 |
15.72*10-3 |
9.96*10-3 |
|
|
|
|
|
36.13*10-3 |
15.16*10-3 |
10.48*10-3 |
|
|
|
4.28 |
4. Przykładowe obliczenia
a) promień pierścienia
[m]
b) promień soczewki R
dla m=35, n=15
[m]
c) wyznaczanie średniej wartości promienia
[m]
5. Rachunek błędów i dyskusja wyników
a) błędy Δrm i Δrn zależące od dokładności nastawienia środka krzyża nici pajęczej w
stosunku do prążka interferencyjnego.
Błąd ten oszacowujemy doświadczalnie przez trzykrotne ustawienie środka krzyża na
środku prążka, odczytanie wskazania mikrometru, obliczenie średniego wskazania.
Maksymalne odstępstwo od średniej przyjmujemy jako (Δl)=(Δp).
(Δrm)=(Δrn)=2∗(Δl)
Pomiary:
[m]
[m]
[m]
Obliczamy wartość średnią:
[m]
(Δl)=(Δp)= [m]
(Δrm)=(Δrn)=2(Δl)= [m]
b) błąd średni kwadratowy:
[m]
ε1 = R1 - Rsr = 4.24 - 4.28 = -0.04 [m]
ε2 = R2 - Rsr = 4.28 - 4.28 = 0 [m]
ε3 = R3 - Rsr = 4.28 - 4.28 = 0 [m]
ε4 = R4 - Rsr = 4.27 - 4.28 = -0.01 [m]
ε5 = R5 - Rsr = 4.30 - 4.28 = 0.02 [m]
ε6 = R6 - Rsr = 4.35 - 4.28 = 0.07 [m]
ε7 = R7 - Rsr = 4.25 - 4.28 = -0.03 [m]
ε8 = R8 - Rsr = 4.29 - 4.28 = 0.01 [m]
ε9 = R9 - Rsr = 4.24 - 4.28 = -0.04 [m]
ε10 = R10 - Rsr = 4.28 - 4.28 = 0 [m]
ΔR = 0.033 [m]
[m]
Dyskusja wyników
Niedokładność pomiarów oraz błędy jakie w czasie tych pomiarów otrzymałem uzależnione są od:
- niedokładności urządzeń pomiarowych - w naszym przypadku mikroskopu
- niedokładności odczytów
- zaokrągleń liczb w czasie wykonywania obliczeń
![]()
Wyszukiwarka
Podobne podstrony:
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko - wypukłej(1), Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko - wypukłej metodą pierścieni Newtona, Sprawozdania - Fizyk
Opt- Pomiar promienia krzywizny soczewki płasko - wypukłej m, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko-wypukłej 2, Sprawozdania - Fizyka
Opt- Pomiar promienia krzywizny soczewki płasko-wypukł metod, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Pomiar promieni krzywizny soczewki płasko-wypukłej metodą pierścieni Newtona, POLITECHNIKA CZ˙STOCHO
Wyznaczania promienia krzywizny soczewki płasko-wypukłej2, Fizyka
Pomiar promieni krzywizny soczewki płasko wypukłej metod DOC
Wyznaczania promieni krzywizny soczewki płasko-wypukłej meto, Akademia Morska Szczecin Nawigacja, uc
OP Pomiar promieniowania krzywizny soczewki, Wiadomo˙ci teoretyczne
sprawka fizyka, Wyznaczanie promienia krzywizny soczewki za pomocą pierścieni Newtona
72a promień krzywizny soczewek, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Lab
POMIAR ODLEGŁOŚCI OGNISKOWYCH SOCZEWEK1, Studia - podręczniki, fizyka, sprawozdania, soczewki, badan
Promie˝ krzywizny soczewki(fiz), Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza l
1, sprawozdanie 81, WYZNACZANIE PROMIENI KRZYWIZNY SOCZEWKI I DŁUGOŚCI FALI ŚWIETLNEJ ZA POMOCĄ PIER
Pomiar odległości ogniskowych soczewek, Pwr MBM, Fizyka, sprawozdania vol I, sprawozdania część I
promień krzywizny soczewek, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolat
więcej podobnych podstron