Wydział: WiŚ	Imie i Nazwisko	Nr. Zepołu 13	Ocena Ostateczna
Grupa: Dziewiąta	Tytół ćwiczenia: Pomiar oporu elektrycznego i wyznaczanie oporu właściwego metali	Nr. Cwiczenia 12	Data Wykonania:

1. Wprowadzenie

Opór elektryczny R jest wielkością charakterystyczną dla danego przewodnika. Zgodnie z prawem Ohma stosunek napięcia U, przyłożonego do końców przewodnika, do natężenia prądu I płynącego przez przewodnika jest wielkością stałą, którą nazywamy oporem elektrycznym R:

Opór przewodnika zależy od jego długości l, przekroju poprzecznego S oraz rodzaju materiału z jakiego wykonany jest przewodnik i wyraża się wzorem:

Występujący we wzorze współczynnik proporcjonalności ρ nosi nazwę oporu właściwego. Ów opór to opór przewodnika o długości 1 metra i polu przekroju 1 metra kwadratowego (sześcian o boku równym 1 m).

Pomiaru oporu elektrycznego można dokonać różnymi sposobami:

- miernikiem elektrycznym odpowiednio wzorcowanym - omomierzem

- z prawa Ohma - mierząc napięcie U i natężenie prądu I

- metodami mostkowymi (np. mostkiem Wheatstone'a dla średnich wartości oporów)

- metodami kompensacyjnymi

• Mostek Wheatstone'a

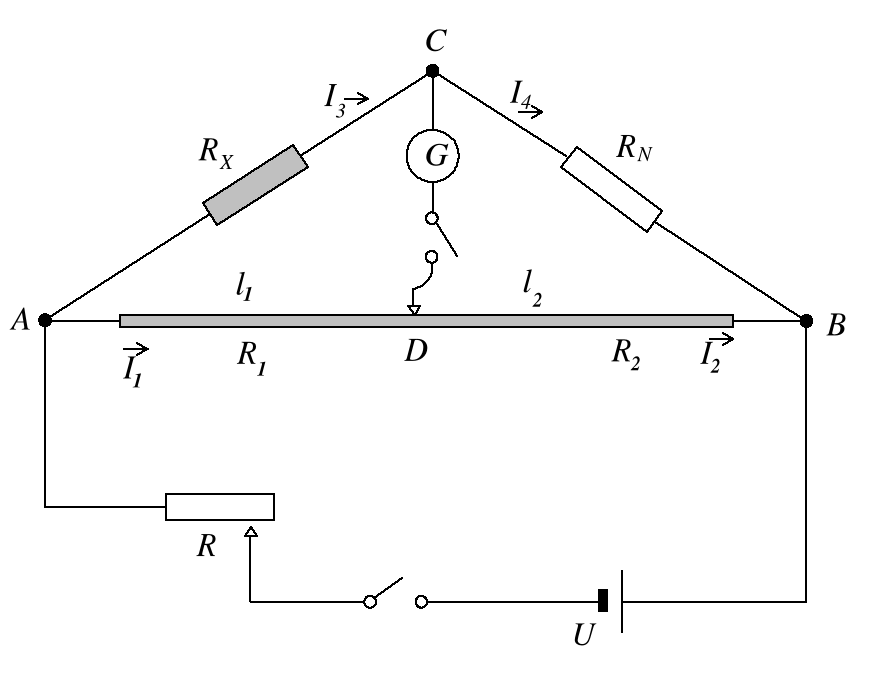
Przedstawiony poniżej obwód jest nazywany mostkiem Wheatstone'a. Odwód mostka składa się z dwóch równoległych gałęzi ACB i ADB.

Między punktami A i B, na podziałce milimetrowej, rozciągnięty jest kalibrowany drut oporowy o długości 1,000 m. W gałęzi AC jest mierzony opór R_X, a w gałęzi CB opór wzorcowy R_N. Między punktem C i suwakiem D wpięty jest galwanometr G o stałej ~ 10^-9 A/dz. Mostek zasilany jest poprzez opór R stałym napięciem U (kilka Voltów).

Pomiar polega na doprowadzeniu mostka do równowagi, która występuje wówczas, gdy przez galwanometr nie płynie prąd. Dokonujemy tego przesuwając styk D wzdłuż drutu AB tak, aby uzyskać
.

Gdy mostek jest w równowadze, to spełnione są wówczas następujące zależności:

oraz równość napięć w gałęziach AC i AD:

i gałęziach CB i DB:

Z powyższych zależności otrzymujemy, że

Położenie styku D dzieli drut AB na odcinki AD = l₁ i DB = l₂. Ponieważ

to mierzony opór R_X obliczamy ze wzoru

Największą czułość mostka otrzymujemy wówczas, gdy
. Dobieramy zatem opór R_N tak, aby był on zbliżony do oporu mierzonego R_X.

2. Metoda pomiaru

Korzystając z prawa z Ohma wyznaczamy opór jednego z drutów w tym celu łączymy układ zgodnie z poniższym schematem.

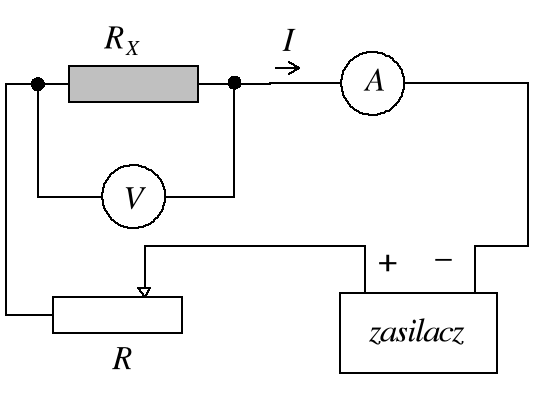
taki układ połączeń stosujemy wówczas, gdy opór mierzony R_X jest dużo mniejszy od oporu woltomierza R_V.

Dokładność oporu R_X obliczamy ze wzoru

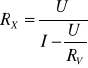
Jeżeli jest spełniony warunek R_X << R_V, mierzony opór dany jest zależnością

Należy wykonać pięć pomiarów oporu R_X, zmieniając oporem R wartość natężenia prądu i napięcia.

3. Tabele pomiarowe i obliczenia.

	Drut pierwszy					Drut drugi
Lp.	[Ω]	[m]	[m]		[Ω]	[Ω]	[m]		[m]		[Ω]
1	5,2	0,493	0,507		5,05	19,3	0,506		0,494		24,56
2	5,3	0,487	0,503		5,03	19,4	0,507		0,493		24,41
3	5,4	0,485	0,508		5,08	19,5	0,506		0,494		24,81
5,05						24,59

	drut pierwszy		drut drugi
Lp.	l [m]	d [mm]	l [m]	d [mm]
1	1,010	0,57	1,765	0,37
2	1,010	0,58	1,765	0,38
3	1,010	0,57	1,765	0,36
4	1,010	0,59	1,765	0,37
5	1,010	0,56	1,765	0,37
6	1,010	0,58	1,765	0,36
7	1,010	0,51	1,765	0,36
8	1,010	0,50	1,765	0,38
9	1,010	0,59	1,765	0,37
10	1,010	0,50	1,765	0,31
	1,010	0,57	1,765	0,37

Podstawiając odpowiednie dane do poniższego wzoru:

Zatem

ρ₁ = 1.206 · 10^-6 Ω·m

ρ₂ = 1,214 · 10^-6 Ω·m

4. Błędy pomiarowe

∆l=0,001m

∆2=0,001m

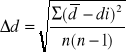
Zatem wyliczona niepewnoś wynosi odpowiednio:

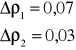
Zatem ostatecznie wyniki są równe:

ρ₁ = [(1,206
0,07 ) · 10^-6 ] Ω·m

ρ₂ = [(1,214
0,03 ) · 10^-6 ] Ω·m

---