Robert Maniura
Sprawozdanie z ćwiczenia nr B-11: Prężność pary nasyconej w układach jednoskładnikowych.
1. Wstęp teoretyczny:
Reguła faz zastosowana do opisu układów jednoskładnikowych stwierdza, że liczba stopni swobody takich układów wynosi 3 - , a zatem, że w układach tych mogą występować jedna, dwie lub maksymalnie trzy fazy.
Jak wynika z reguły faz, układ jednoskładnikowy, w którym występują dwie fazy, wykazuje jeden stopień swobody (s = 1 - 2 + 2). Oznacza to, że z dwóch zmiennych intensywnych opisujących stan takiego układu (temperatury i ciśnienia) jedną można traktować jako niezależną, druga powiązana jest z nią zależnością funkcyjną. Linia równowagi fazowej wykresem tej zależności. Ustalając np. dowolną wartość temperatury T1 można odszukać na linii równowagi punkt o współrzędnych (T1, p1) dla którego spełniony jest warunek równowagi fazowej:
![]()
Zajmiemy się obecnie wyprowadzeniem analitycznej postaci zależności funkcyjnej pomiędzy ciśnieniem i temperaturą w stanie równowagi dwufazowej, której geometrycznym obrazem jest linia równowagi. Zależność ta znana jest pod nazwą prawa Clausiusa - Clapeyrona. Punkt wyjścia stanowi znów termodynamiczny warunek równowagi izotermiczno - izobarycznej między fazami k i j:
![]()
Podziałajmy na układ zawierający obie te fazy w równowadze jakimś czynnikiem z zewnątrz. Niech tym czynnikiem będzie np. dostarczenie ciepła, zwiększające temperaturę układu o wartość dT. Pociągnie to za sobą odpowiednią zmianę ciśnienia w układzie o wartość dp, układ jest bowiem jednozmienny. Odpowiednio do tych zmian również wartości molowych entalpii swobodnych obu faz zmienią się o dGk i dGj. Zmiany te można wyrazić równaniami:
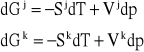
Ponieważ układ w nowym stanie pozostaje nadal w równowadze fazowej, wartości molowych entalpii swobodnych obu faz będą nadal sobie równe, aczkolwiek będą się nieco różniły od wartości poprzednich. Oznacza to, że zmiany dGk i dGj muszą być sobie równe, co możemy zapisać w postaci następującego równania:
![]()
Po przekształceniu otrzymujemy różniczkową postać zależności funkcyjnej między p i T w stanie równowagi:
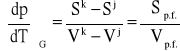
którą na podstawie wzoru Sp.f. = Hp.f./Tp.f. można zapisać alternatywnie w postaci równań:
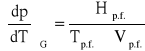
(1)
oraz
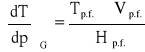
(2)
Dwa ostatnie równania stanowią dwie równoważne formy prawa Clausiusa - Clapeyrona, wiążącego wartości ciśnienia i temperatury w układzie jednoskładnikowym, w którym w stanie równowagi znajdują się dwie fazy. Gdy jedną z faz stanowi para nasycona, tj. gdy rozważa się równowagę parowania lub sublimacji, dogodniej jest posłużyć się równaniem pierwszym. Otrzymuje się z niego, dającą się bezpośrednio sprawdzić doświadczalnie, relację między prężnością pary nasyconej p a temperaturą T, która panuje w układzie. Dyskutując zachowanie się układu złożonego z dwóch faz skondensowanych, a więc rozważając proces topnienia, krzepnięcia lub przemiany polimorficznej, wygodniej jest posłużyć się postacią drugą. Określa ona, w jaki sposób temperatura równowagi T (np. temperatura topnienia) zależy od panującego w układzie ciśnienia p. Stosując równanie pierwsze do opisu równowagi parowania lub sublimacji, można przekształcić je do postaci całkowalnej. W tym celu korzysta się z przybliżeń i otrzymuje:
![]()
a w konsekwencji:
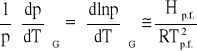
Przy dodatkowym założeniu niezależności ciepła parowania (sublimacji) od temperatury, równanie drugie daje się łatwo scałkować. Otrzymuje się wówczas wyrażenie przedstawiające ciśnienie pary nasyconej nad cieczą lub fazą stalą (p) jako funkcję temperatury (T):
![]()
(3)
przy czym wartość stałej całkowania zależna jest od rodzaju substancji oraz od jednostek, w jakich wyrażone jest ciśnienie.
Zauważono, że iloraz standardowego ciepła parowania w temperaturze wrzenia i normalnej temperatury wrzenia, tj. temperatury wrzenia pod ciśnieniem 1 atm, ma dla wielu substancji wartość podobną (reguła Troutona):
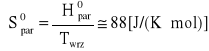
Równanie (3) przewiduje liniową zależność logarytmu prężności pary nasyconej od odwrotności temperatury bezwzględnej, stwierdzoną rzeczywiście w doświadczeniach przeprowadzanych w niezbyt szerokim zakresie temperatur. Pewne zakrzywienie linii log p = f(1/T), widoczne w dokładniejszych pomiarach, jest zrozumiale wobec uproszczeń poczynionych w trakcie wyprowadzania wzoru (1). Ściśle rzecz biorąc niepoprawne jest bowiem zarówno założenie stałości Hp.r.* (np. ciepło parowania wody w pobliżu temp. l00oC maleje w przybliżeniu o 0,12 % ze wzrostem temperatury o 1 stopień), jak i użycie równania stanu gazu doskonałego do opisu własności pary nasyconej. Mimo tych uproszczeń wzór (2) jest często stosowany do interpolacji i ekstrapolacji wyników pomiarów prężności pary nasyconej do innych wartości temperatury. Często korzysta się też z niego obliczając ciepło parowania (sublimacji) na podstawie wyznaczanych doświadczalnie wartości prężności pary nasyconej w kilku temperaturach.
Linia równowagi pomiędzy fazą ciekłą i parą wykazuje ciekawą osobliwość, nie obserwowaną dla linii równowagi pomiędzy jakimikolwiek innymi dwiema fazami. Jej zasięg na wykresie p(T) jest mianowicie ograniczony w kierunku rosnących temperatur wartością temperatury krytycznej danej cieczy. W tej temperaturze zanikają różnice pomiędzy stanami: ciekłymi gazowym, powierzchnie entalpii swobodnej obu tych faz schodzą się z sobą i dalej, w wyższych temperaturach i ciśnieniach, przebiegają wspólnie jako jedna powierzchnia, odpowiadająca fazie "nadkrytycznej". W przypadku równowagi pomiędzy parą nasyconą i fazą stalą lub ciekłą, zwiększenie temperatury wywołuje zawsze zwiększenie ciśnienia w układzie (prężności pary nasyconej), to znaczy na wykresie P(T) linia równowagi wykazuje nachylenie dodatnie. Wynika to z faktu, że zarówno objętość, jak i entalpia molowa fazy gazowej są zawsze większe od tychże wielkości dla fazy skondensowanej [Vp.r. i Hp.r. są dodatnie i w konsekwencji pochodna (dp/dT)G jest również dodatnia]. Inaczej ma się rzecz z linią równowagi między dwiema fazami skondensowanymi: cieczą i ciałem stałym, lub dwiema odmianami polimorficznymi. Tutaj również faza trwalsza w wyższej temperaturze wykazuje zazwyczaj wyższą wartość entalpii molowej, jednakże DVpf. może być zarówno dodatnie, jak i ujemne. W zależności od znaku DVpf. pochodna (dT/dp)G będzie miała znak dodatni lub ujemny, to znaczy zwiększenie ciśnienia w układzie powodować będzie zwiększenie lub zmniejszenie temperatury przemiany (równowagi fazowej). Jeżeli zdarzy się, że objętości molowe obu faz skondensowanych są jednakowe, linia p(T) przebiega na wykresie pionowo - wartość ciśnienia nie ma wpływu na temperaturę przemiany fazowej. Ciecze wykazują zazwyczaj mniejszą gęstość (większą objętość właściwą) niż faza stała, z której powstały. Z tego względu linia topnienia na wykresie p(T) ma zazwyczaj nachylenie dodatnie. Wyjątek stanowią między innymi woda, bizmut, german i gal, dla których stwierdza się obniżenie temperatury topnienia pod zwiększonym ciśnieniem (w zakresie nie nadmiernie wysokich ciśnień).
Opracowanie wyników:
Pomiaru temperatury wrzenia dokonane zostały przy różnych wartościach ciśnienia po osiągnięciu temperatury wrzenia i ustabilizowaniu się wskazań termometru oraz manometru. Wartość ciśnienia dla danej temperatury obliczam z równania kalibracyjnego manometru:
p [hPa] = 953,3 + 544,3 U + 13,56 U2 gdzie: U - wskazania miernika ciśnienia [mV]
Pomiar 1
L.p. |
t [°C] |
T [K] |
1/T |
U [V] |
p [hPa] |
P = p/po |
lnP |
1. |
65 |
338,15 |
0,002957 |
-1,389 |
223,428893 |
0,220562 |
-1,51158 |
2. |
67 |
340,15 |
0,00294 |
-1,345 |
245,746879 |
0,242593 |
-1,41637 |
3. |
69 |
342,15 |
0,002923 |
-1,282 |
277,793585 |
0,274229 |
-1,29379 |
4. |
71 |
344,15 |
0,002906 |
-1,266 |
285,949571 |
0,28228 |
-1,26486 |
5. |
72 |
345,15 |
0,002897 |
-1,228 |
305,347863 |
0,301429 |
-1,19922 |
6. |
75 |
348,15 |
0,002872 |
-1,146 |
347,340765 |
0,342883 |
-1,07037 |
7. |
77 |
350,15 |
0,002856 |
-1,094 |
374,064896 |
0,369264 |
-0,99624 |
8. |
79 |
352,15 |
0,00284 |
-1,08 |
381,272384 |
0,376379 |
-0,97716 |
9. |
81 |
354,15 |
0,002824 |
-0,973 |
436,533745 |
0,430932 |
-0,84181 |
10. |
83 |
356,15 |
0,002808 |
-0,902 |
473,37387 |
0,467299 |
-0,76079 |
11. |
85 |
358,15 |
0,002792 |
-0,828 |
511,916119 |
0,505347 |
-0,68251 |
12. |
87 |
360,15 |
0,002777 |
-0,751 |
552,178554 |
0,545092 |
-0,6068 |
13. |
89 |
362,15 |
0,002761 |
-0,666 |
596,810819 |
0,589152 |
-0,52907 |
14. |
91 |
364,15 |
0,002746 |
-0,572 |
646,397015 |
0,638102 |
-0,44926 |
15. |
93 |
366,15 |
0,002731 |
-0,47 |
700,474404 |
0,691485 |
-0,36891 |
16. |
95 |
368,15 |
0,002716 |
-0,378 |
749,492107 |
0,739874 |
-0,30128 |
17. |
97 |
370,15 |
0,002702 |
-0,276 |
804,106147 |
0,793787 |
-0,23094 |
18. |
99 |
372,15 |
0,002687 |
-0,18 |
855,765344 |
0,844783 |
-0,16868 |
19. |
100 |
373,15 |
0,00268 |
-0,13 |
882,770164 |
0,871441 |
-0,13761 |
Równanie regresji liniowej prostej ln p = f (1/T ) z wykresu tej zależności:
y |
a |
x |
b |
y=ax+b |
ln p |
-4955,8 |
1/T |
13,153 |
ln p =-4955,8/T+13,153 |
Normalna temperatura wrzenia: ln p = 0
0 = -4955,8/T + 13,153 => T0 = 376,78 [K]
Molowa entalpia parowania:
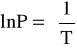
z równania Clausiusa- Clapeyrona po całkowaniu:
![]()
gdzie: a = -4955,8; R = 8,314 [J/(mol-*K)]
![]()
Molowa entropia parowania:
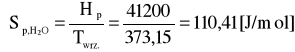
Pomiar 2
L.p. |
t [°C] |
T [K] |
1/T |
U [V] |
p [hPa] |
P = p/po |
lnP |
1. |
63 |
336,15 |
0,002975 |
-1,43 |
202,6798 |
0,200079 |
-1,60904 |
2. |
65 |
338,15 |
0,002957 |
-1,388 |
223,9355 |
0,221062 |
-1,50931 |
3. |
68 |
341,15 |
0,002931 |
-1,338 |
249,3023 |
0,246103 |
-1,40201 |
4. |
70 |
343,15 |
0,002914 |
-1,293 |
272,1904 |
0,268697 |
-1,31417 |
5. |
72 |
345,15 |
0,002897 |
-1,251 |
293,6021 |
0,289834 |
-1,23845 |
6. |
74 |
347,15 |
0,002881 |
-1,195 |
322,2255 |
0,31809 |
-1,14542 |
7. |
76 |
349,15 |
0,002864 |
-1,136 |
352,4743 |
0,347951 |
-1,05569 |
8. |
78 |
351,15 |
0,002848 |
-1,068 |
387,4545 |
0,382482 |
-0,96107 |
9. |
80 |
353,15 |
0,002832 |
-1,018 |
413,2552 |
0,407952 |
-0,89661 |
10. |
82 |
355,15 |
0,002816 |
-0,951 |
447,9344 |
0,442186 |
-0,81602 |
11. |
84 |
357,15 |
0,0028 |
-0,875 |
487,4194 |
0,481164 |
-0,73155 |
12. |
86 |
359,15 |
0,002784 |
-0,802 |
525,4932 |
0,51875 |
-0,65633 |
13. |
88 |
361,15 |
0,002769 |
-0,717 |
570,0079 |
0,562693 |
-0,57502 |
14. |
90 |
363,15 |
0,002754 |
-0,63 |
615,773 |
0,607871 |
-0,49779 |
15. |
92 |
365,15 |
0,002739 |
-0,544 |
661,2137 |
0,652728 |
-0,42659 |
16. |
94 |
367,15 |
0,002724 |
-0,433 |
720,1605 |
0,710919 |
-0,3412 |
17. |
96 |
369,15 |
0,002709 |
-0,355 |
761,7824 |
0,752006 |
-0,28501 |
18. |
98 |
371,15 |
0,002694 |
-0,246 |
820,2228 |
0,809697 |
-0,2111 |
19. |
100 |
373,15 |
0,00268 |
-0,192 |
849,2943 |
0,838395 |
-0,17627 |
20 |
102 |
375,15 |
0,002666 |
-0,128 |
883,8518 |
0,872509 |
-0,13638 |
Równanie regresji liniowej prostej ln p = f (1/T ) z wykresu tej zależności:
y |
a |
x |
b |
y=ax+b |
ln p |
-4920,5 |
1/T |
13,035 |
ln p =-4920,5/T+13,035 |
Normalna temperatura wrzenia: ln p = 0
0 = -4920,5/T + 13,035 => T0 = 377,48 [K]
Molowa entalpia parowania:
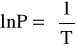
z równania Clausiusa- Clapeyrona po całkowaniu:
![]()
gdzie: a = -4920,5; R = 8,314 [J/(mol-*K)]
![]()
Molowa entropia parowania:
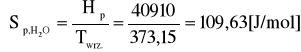
Zestawienie wyników i porównanie z wartościami tablicowymi:
L.p. |
Normalna temperatura wrzenia [K] |
Molowa entalpia parowania [kJ/mol] |
Molowa entropia parowania [J/K] |
1. wartość wyznaczona (pomiar 1) |
376,78 |
41,20 |
110,41 |
2. wartość wyznaczona (pomiar 2) |
377,48 |
40,91 |
109,63 |
3. wartość wyznaczona (średnia) |
377,13 |
41,06 |
110,02 |
4. wartość tablicowa |
373,15 |
40,66 |
109,13 |
5. błąd procentowy |
1,07 % |
0,98 % |
0,81 % |
4. Wnioski:
Entropia parowania jest wielkością związaną ze strukturą cieczy. Według reguły Troutona entropia parowania cieczy niezasocjowanych jest stała i wynosi ok. 88 [J/K]. Wartość otrzymana w pomiarze jest znacznie wyższa od wartości, która wynika z reguły Troutona. Świadczy to o silnej asocjacji wody. Wyznaczona normalna temperatura wrzenia wody (377,13 K) niewiele różni się od wartości tablicowej (373,15 K - błąd względny 1,07 %). Otrzymana z pomiarów wartość molowej entalpii parowania wody - 41,06 kJ/mol - jest nieco wyższa od wartości literaturowej (40,66 kJ/mol - błąd względny 0,98 %).
3
Wyszukiwarka
Podobne podstrony:
Prężność pary nasyconej w układach jednoskładnikowych
zadania2 preznosc pary nasyconej oraz gestosc cieczy i gazow, Technologia chemiczna, Podstawy techno
Fizyczna prężność pary nasyconej
Prężność pary nasyconej
Prężność pary nasyconej
badanie ruchu jednost przysp, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 1 semestr
Prawo inżynierskie i ochrona własności intelektualnych. Wykład 3, Studia, Politechnika Łódzka - Pend
Testy biodegradacji, Studia, Politechnika
Chf9, Studia, Politechnika
Wyznaczanie stałej reakcji szybkości zmydlania estru, Studia, Politechnika
CH.F.L9, Studia, Politechnika
ZAKAAD CHEMI FIZYCZNEJ, Studia, Politechnika
C15, Studia, Politechnika
podstawowe informacje o ochronie prawnej wzorów przemysłowych, Studia - Politechnika Śląska, Zarządz
Sprawko spawalnictwo 1, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 2 semestr, obro
dziadek25, Studia, Politechnika
Cisnienie pary nasyconej
4 2 vademecum echosondy (w tym przykładzie wodnej), studia, studia Politechnika Poznańska - BMiZ - M
więcej podobnych podstron