MOC PRĄDÓW ODKSZTAŁCONYCH.

Moc czynna dwójnika równa się sumie mocy wytworzonej przez składowe stałe U₀, I₀ oraz mocy czynnych poszczególnych harmonicznych prądu i napięcia tego samego rzędu: P=U₀I₀+_k=1Σ^∞U_k⋅I_k⋅cosϕ_k. Moc bierną definiujemy jako sumę mocy biernych poszczególnych harmonicznych: P= _k=1Σ^∞U_k⋅I_k⋅sinϕ_k. Mocą pozorną nazywamy iloczyn wartości skutecznych prądu i napięcia: S_p=U_skI_sk. Moc odkształcenia: Dla niesinusoidalnych przebiegów ogólnie nie obowiązuje trójkąt mocy. Zachodzi natomiast nierówność: P²+Q²≤S_p², w związku z czym wprowadza się pojęcie mocy zniekształcenia T, korzystając z relacji: P²+Q²+T²=S_p².

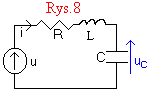
STAN NIEUSTALONY W SZEREGOWYM OBWODZIE RLC.

W celu sformułowania równania obwodu zastosujemy NPK:

Ri + L(di/dt) + u_C = u,

i podstawimy i=C(du_C/dt), otrzymując: LC(d²u_CS/dt²) + RC(du_CS/dt) + u_CS = 0. Równanie to zapiszemy w postaci:

(1) (d²u_CS/dt²) + 2α(du_CS/dt) + ω_n²uCS = 0, gdzie α=R/2L nosi nazwę stałej tłumienia, zaś ω_n = 1/√(LC) jest pulsacją drgań nietłumionych. Rozwiązanie równania (1) zależy od pierwiastków równania charakterystycznego s²+2αs+ω_n²=0, wynoszących:

s_1,2 = -α ± √(α²-ω_n²). Rozróżniamy trzy przypadki:

1) α>ω_n, czyli R>2√(L/C) - pierwiastki równania charakterystycznego są rzeczywiste i ujemne, a ponadto s₁≠s₂. Rozwiązanie swobodne określa wzór:

u_CS = A₁e^s1t+A₂e^s2t, zaś: i_S = C(dU_CS/dt) = C(A₁s₁e^s1t+A₂s₂e^s2t), przy czym A₁ i A₂ są stałymi zależnymi od warunków początkowych. Przebiegi mają charakter aperiodyczny i znikają od zera dla t→∞.

2) α=ω_n, czyli R=2√(L/C) - pierwiastki równania charakterystycznego są jednakowe, rzeczywiste i ujemne, a ponadto s₁ = s₂ = -α. Rozwiązanie jest następujące: u_CS = (A₁+A₂t)e^-αt, a zatem:

i_S = C(dU_CS/dt) = C[A₂-α(A₁+A₂t)]e^-αt. Przebiegi aperiodyczne, graniczne, zanikające do zera dla t→∞. 3) α<ω_n, czyli R<2√(L/C) - pierwiastki równania charakterystycznego są zespolone, sprzężone s_1,2 = -α ± jω₀, gdzie ω₀ = √(ω_n²-α²) nosi nazwę pulsacji drgań własnych. Rozwiązanie równania ma postać: u_CS = Ae^-αtsin(ω₀t+ψ), gdzie A i ψ są stałymi. Stąd: i_S = C(dU_CS/dt) = CA[-αsin(ω₀t+ψ) + ω₀cos(ω₀t+ψ)]. Otrzymujemy ostatecznie: i_S = A√(L/C)e^-αtcos(ω₀t+ψ+η), przy czym: η = arctg(α/ω₀). Stopień tłumienia określa dekrement tłumienia ∂. Dla napięcia swobodnego u_CS otrzymujemy: ∂ = u_CS(t)/u_CS(t+T₀) = e^αTo, a stąd wynika następujący wzór na logarytmiczny dekrement tłumienia: ln∂ = αT₀.

TWIERDZENIA PRZEKSZTAŁCENIA LAPLACE'A:

Twierdzenie o liniowości. Jeżeli a i b są dowolnymi stałymi, to α{af(t)+bg(t)}= aF(s)+bG(s). Prawdziwość twierdzenia wynika bezpośrednio z faktu, że całkowanie jest operacją addytywną i jednorodną.

Twierdzenie o podobieństwie. Jeżeli a jest liczbą rzeczywistą dodatnią, to α{f(at)} = (1/a)F(s/a).

Twierdzenie o przesunięciu w dziedzinie zespolonej. Jeżeli k jest dowolną liczbą rzeczywistą lub zespoloną, to α{e^ktf(t)} = F(s-k). Twierdzenie to pokazuje jaki wpływ w dziedzinie przekształcenia Laplace'a ma pomnożenie funkcji f(t) przez czynnik e^kt.

Twierdzenie o opóźnieniu. Jeżeli h jest stałą rzeczywistą dodatnią, to α{f(t-h)u(t-h)} = e^-shF(s).

Twierdzenie o transformacie pochodnej. α{df/dt} = sF(s)-f(0), gdy F(s) = α{f(t).

Twierdzenie o transformacie całki. α{₀∫^t f(τ)dτ} = F(s)/s, gdy F(s) = α{f(t).

Twierdzenie o transformacie splotu (Borela). α{f(t)*g(t)} = F(s)G(s).

CZWÓRNIKI.

Czwórnik - połączenie mające cztery zaciski: dwa zaciski wejściowe (pierwotne) oraz dwa zaciski wyjściowe (wtórne). Zaciski wejściowe oznaczamy 1, 1', a wyjściowe 2, 2'. Napięcie u₁ między 1,1' nazywa się wejściowym, natomiast u₂ między 2,2' - wyjściowym. Podobnie prądu i₁ oraz i₂.

Czwórnik liniowy - gdy wszystkie elementy z których zbudowany jest czwórnik są liniowe.

Czwórnik nieliniowy - jeżeli choć jeden z elementów jest nieliniowy.

Czwórnik aktywny - jeżeli w wewnętrznych połączeniach znajdują się niezależne źródła energii. Czwórnik nie zawierający żadnego źródła nazywa się pasywnym.

POŁĄCZENIE SZEREGOWE I RÓWNOLEGŁE CZWÓRNIKÓW:

Połączenie szeregowe (regularne): Równania impedancyjne poszczególnych czwórników w połączeniu przybierają postać: [U₁'; U₂'] = z₁[I₁; I₂] oraz [U₁''; U₂''] = z₂[I₁; I₂]. Napięcie wejściowe U₁ oraz wyjściowe U₂ są sumą napięć po stronie wejściowej lub wyjściowej obu czwórników. Wynika stąd, że macierz impedancyjna połączenia szeregowego dwóch czwórników: z = z₁+z₂, a więc macierze impedancyjne dodają się.

Połączenie równoległe: W połączeniu równoległym dwóch czwórników zarówno strony wejściowe jak i wyjściowe obu czwórników połączone są równolegle, wobec czego napięcie U₁ istnieje po stronie wejściowej, a napięcie U₂ - po stronie wyjściowej każdego z czwórników. Równania admitancyjne poszczególnych czwórników tworzących połączenie wyrażają się wzorami: [I₁'; I₂'] = y₁[U₁; U₂] oraz [I₁''; I₂''] = y₂[U₁; U₂]. Macierz admitancyjna połączenia równoległego dwóch czwórników: y = y₁+y₂, co oznacza że przy połączeniu równoległym czwórników dodają się ich macierze admitancyjne.

MOC PRĄDÓW ODKSZTAŁCONYCH.

Moc czynna dwójnika równa się sumie mocy wytworzonej przez składowe stałe U₀, I₀ oraz mocy czynnych poszczególnych harmonicznych prądu i napięcia tego samego rzędu: P=U₀I₀+_k=1Σ^∞U_k⋅I_k⋅cosϕ_k. Moc bierną definiujemy jako sumę mocy biernych poszczególnych harmonicznych: P= _k=1Σ^∞U_k⋅I_k⋅sinϕ_k. Mocą pozorną nazywamy iloczyn wartości skutecznych prądu i napięcia: S_p=U_skI_sk. Moc odkształcenia: Dla niesinusoidalnych przebiegów ogólnie nie obowiązuje trójkąt mocy. Zachodzi natomiast nierówność: P²+Q²≤S_p², w związku z czym wprowadza się pojęcie mocy zniekształcenia T, korzystając z relacji: P²+Q²+T²=S_p².

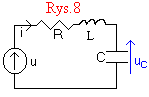
STAN NIEUSTALONY W SZEREGOWYM OBWODZIE RLC.

W celu sformułowania równania obwodu zastosujemy NPK:

Ri + L(di/dt) + u_C = u,

i podstawimy i=C(du_C/dt), otrzymując: LC(d²u_CS/dt²) + RC(du_CS/dt) + u_CS = 0. Równanie to zapiszemy w postaci:

(1) (d²u_CS/dt²) + 2α(du_CS/dt) + ω_n²uCS = 0, gdzie α=R/2L nosi nazwę stałej tłumienia, zaś ω_n = 1/√(LC) jest pulsacją drgań nietłumionych. Rozwiązanie równania (1) zależy od pierwiastków równania charakterystycznego s²+2αs+ω_n²=0, wynoszących:

s_1,2 = -α ± √(α²-ω_n²). Rozróżniamy trzy przypadki:

1) α>ω_n, czyli R>2√(L/C) - pierwiastki równania charakterystycznego są rzeczywiste i ujemne, a ponadto s₁≠s₂. Rozwiązanie swobodne określa wzór:

u_CS = A₁e^s1t+A₂e^s2t, zaś: i_S = C(dU_CS/dt) = C(A₁s₁e^s1t+A₂s₂e^s2t), przy czym A₁ i A₂ są stałymi zależnymi od warunków początkowych. Przebiegi mają charakter aperiodyczny i znikają od zera dla t→∞.

2) α=ω_n, czyli R=2√(L/C) - pierwiastki równania charakterystycznego są jednakowe, rzeczywiste i ujemne, a ponadto s₁ = s₂ = -α. Rozwiązanie jest następujące: u_CS = (A₁+A₂t)e^-αt, a zatem:

i_S = C(dU_CS/dt) = C[A₂-α(A₁+A₂t)]e^-αt. Przebiegi aperiodyczne, graniczne, zanikające do zera dla t→∞. 3) α<ω_n, czyli R<2√(L/C) - pierwiastki równania charakterystycznego są zespolone, sprzężone s_1,2 = -α ± jω₀, gdzie ω₀ = √(ω_n²-α²) nosi nazwę pulsacji drgań własnych. Rozwiązanie równania ma postać: u_CS = Ae^-αtsin(ω₀t+ψ), gdzie A i ψ są stałymi. Stąd: i_S = C(dU_CS/dt) = CA[-αsin(ω₀t+ψ) + ω₀cos(ω₀t+ψ)]. Otrzymujemy ostatecznie: i_S = A√(L/C)e^-αtcos(ω₀t+ψ+η), przy czym: η = arctg(α/ω₀). Stopień tłumienia określa dekrement tłumienia ∂. Dla napięcia swobodnego u_CS otrzymujemy: ∂ = u_CS(t)/u_CS(t+T₀) = e^αTo, a stąd wynika następujący wzór na logarytmiczny dekrement tłumienia: ln∂ = αT₀.

TWIERDZENIA PRZEKSZTAŁCENIA LAPLACE'A:

Twierdzenie o liniowości. Jeżeli a i b są dowolnymi stałymi, to α{af(t)+bg(t)}= aF(s)+bG(s). Prawdziwość twierdzenia wynika bezpośrednio z faktu, że całkowanie jest operacją addytywną i jednorodną.

Twierdzenie o podobieństwie. Jeżeli a jest liczbą rzeczywistą dodatnią, to α{f(at)} = (1/a)F(s/a).

Twierdzenie o przesunięciu w dziedzinie zespolonej. Jeżeli k jest dowolną liczbą rzeczywistą lub zespoloną, to α{e^ktf(t)} = F(s-k). Twierdzenie to pokazuje jaki wpływ w dziedzinie przekształcenia Laplace'a ma pomnożenie funkcji f(t) przez czynnik e^kt.

Twierdzenie o opóźnieniu. Jeżeli h jest stałą rzeczywistą dodatnią, to α{f(t-h)u(t-h)} = e^-shF(s).

Twierdzenie o transformacie pochodnej. α{df/dt} = sF(s)-f(0), gdy F(s) = α{f(t).

Twierdzenie o transformacie całki. α{₀∫^t f(τ)dτ} = F(s)/s, gdy F(s) = α{f(t).

Twierdzenie o transformacie splotu (Borela). α{f(t)*g(t)} = F(s)G(s).

CZWÓRNIKI.

Czwórnik - połączenie mające cztery zaciski: dwa zaciski wejściowe (pierwotne) oraz dwa zaciski wyjściowe (wtórne). Zaciski wejściowe oznaczamy 1, 1', a wyjściowe 2, 2'. Napięcie u₁ między 1,1' nazywa się wejściowym, natomiast u₂ między 2,2' - wyjściowym. Podobnie prądu i₁ oraz i₂.

Czwórnik liniowy - gdy wszystkie elementy z których zbudowany jest czwórnik są liniowe.

Czwórnik nieliniowy - jeżeli choć jeden z elementów jest nieliniowy.

Czwórnik aktywny - jeżeli w wewnętrznych połączeniach znajdują się niezależne źródła energii. Czwórnik nie zawierający żadnego źródła nazywa się pasywnym.

POŁĄCZENIE SZEREGOWE I RÓWNOLEGŁE CZWÓRNIKÓW:

Połączenie szeregowe (regularne): Równania impedancyjne poszczególnych czwórników w połączeniu przybierają postać: [U₁'; U₂'] = z₁[I₁; I₂] oraz [U₁''; U₂''] = z₂[I₁; I₂]. Napięcie wejściowe U₁ oraz wyjściowe U₂ są sumą napięć po stronie wejściowej lub wyjściowej obu czwórników. Wynika stąd, że macierz impedancyjna połączenia szeregowego dwóch czwórników: z = z₁+z₂, a więc macierze impedancyjne dodają się.

Połączenie równoległe: W połączeniu równoległym dwóch czwórników zarówno strony wejściowe jak i wyjściowe obu czwórników połączone są równolegle, wobec czego napięcie U₁ istnieje po stronie wejściowej, a napięcie U₂ - po stronie wyjściowej każdego z czwórników. Równania admitancyjne poszczególnych czwórników tworzących połączenie wyrażają się wzorami: [I₁'; I₂'] = y₁[U₁; U₂] oraz [I₁''; I₂''] = y₂[U₁; U₂]. Macierz admitancyjna połączenia równoległego dwóch czwórników: y = y₁+y₂, co oznacza że przy połączeniu równoległym czwórników dodają się ich macierze admitancyjne.

---