CHARAKTERYSTYKA ODKSZTAŁCENIA.

-Wartość średnia za okres funkcji f(t) definiuje zależność

-Wartość średnia z modułu funkcji

-Wartość skuteczna

- Współczynnik szczytu: Jest to stosunek wartości maksymalnej do skutecznej: s=A_max/A_sk; dla sinusoidy: A_sk=A_max/√2, s=√2; dla prostokąta: A_max=A; A_sk=A; s=1.

- Współczynnik kształtu: Jest to stosunek wartości skutecznej do wartości średniej z modułu: k=A_sk/A_śr; dla sinusoidy: A_śr = 2A_max/π; k = (A_max/√2)(π/2A_max) = 1,11; dla prostokąta: k = A/A = 1.

- Współczynnik zawartości harmonicznych: Jest to stosunek wartości skutecznej przebiegu po usunięciu z niego składowej stałej i pierwszej harmonicznej do wartości skutecznej przebiegu po usunięci z niego składowej stałej: dla sinusoidy: h=0; dla prostokąta: A₀=0; A_sk=A; h=0,43.

- Współczynnik odkształcenia: Jest to stosunek wartości skutecznej I harmonicznej do wartości skutecznej całego przebiegu: k₀ = A₁/A_sk; dla sinusoidy: k₀=A/A=1; dla prostokąta: k₀ = 4/π√2 = 0,9.

- Współczynnik zawartości k-tej harmonicznej: Jest to stosunek wartości skutecznych k-tej harmonicznej do I harmonicznej: h_k = A_k/A₁.

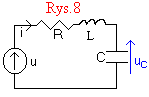
STAN NIEUSTALONY W SZEREGOWYM OBWODZIE RLC.

W celu sformułowania równania obwodu zastosujemy NPK: Ri + L(di/dt) + u_C = u, i podstawimy i=C(du_C/dt), otrzymując LC(d²u_CS/dt²) + RC(du_CS/dt) + u_CS = 0. Równanie to zapiszemy w postaci: (1) (d²u_CS/dt²) + 2α(du_CS/dt) + ω_n²uCS = 0, gdzie α=R/2L nosi nazwę stałej tłumienia, zaś ω_n = 1/√(LC) jest pulsacją drgań nietłumionych. Rozwiązanie równania (1) zależy od pierwiastków równania charakterystycznego s²+2αs+ω_n²=0, wynoszących: s_1,2 = -α ± √(α²-ω_n²). Rozróżniamy trzy przypadki:

1) α>ω_n, czyli R>2√(L/C) - pierwiastki równania charakterystycznego są rzeczywiste i ujemne, a ponadto s₁≠s₂. Rozwiązanie swobodne określa wzór: u_CS = A₁e^s1t+A₂e^s2t, zaś: i_S = C(dU_CS/dt) = C(A₁s₁e^s1t+A₂s₂e^s2t), przy czym A₁ i A₂ są stałymi zależnymi od warunków początkowych. Przebiegi mają charakter aperiodyczny i znikają od zera dla t→∞.

2) α=ω_n, czyli R=2√(L/C) - pierwiastki równania charakterystycznego są jednakowe, rzeczywiste i ujemne, a ponadto s₁ = s₂ = -α. Rozwiązanie jest następujące: u_CS = (A₁+A₂t)e^-αt, a zatem: i_S = C(dU_CS/dt) = C[A₂-α(A₁+A₂t)]e^-αt. Przebiegi aperiodyczne, graniczne, zanikające do zera dla t→∞.

3) α<ω_n, czyli R<2√(L/C) - pierwiastki równania charakterystycznego są zespolone, sprzężone s_1,2 = -α ± jω₀, gdzie ω₀ = √(ω_n²-α²) nosi nazwę pulsacji drgań własnych. Rozwiązanie równania ma postać: u_CS = Ae^-αtsin(ω₀t+ψ), gdzie A i ψ są stałymi. Stąd: i_S = C(dU_CS/dt) = CA[-αsin(ω₀t+ψ) + ω₀cos(ω₀t+ψ)]. Otrzymujemy ostatecznie: i_S = A√(L/C)e^-αtcos(ω₀t+ψ+η), przy czym: η = arctg(α/ω₀). Stopień tłumienia określa dekrement tłumienia ∂. Dla napięcia swobodnego u_CS otrzymujemy: ∂ = u_CS(t)/u_CS(t+T₀) = e^αTo, a stąd wynika następujący wzór na logarytmiczny dekrement tłumienia: ln∂ = αT₀.

TWIERDZENIA PRZEKSZTAŁCENIA LAPLACE'A:

Twierdzenie o liniowości. Jeżeli a i b są dowolnymi stałymi, to α{af(t)+bg(t)}= aF(s)+bG(s). Prawdziwość twierdzenia wynika bezpośrednio z faktu, że całkowanie jest operacją addytywną i jednorodną.

Twierdzenie o podobieństwie. Jeżeli a jest liczbą rzeczywistą dodatnią, to α{f(at)} = (1/a)F(s/a).

Twierdzenie o przesunięciu w dziedzinie zespolonej. Jeżeli k jest dowolną liczbą rzeczywistą lub zespoloną, to α{e^ktf(t)} = F(s-k). Twierdzenie to pokazuje jaki wpływ w dziedzinie przekształcenia Laplace'a ma pomnożenie funkcji f(t) przez czynnik e^kt.

Twierdzenie o opóźnieniu. Jeżeli h jest stałą rzeczywistą dodatnią, to α{f(t-h)u(t-h)} = e^-shF(s).

Twierdzenie o transformacie pochodnej. α{df/dt} = sF(s)-f(0), gdy F(s) = α{f(t).

Twierdzenie o transformacie całki. α{₀∫^t f(τ)dτ} = F(s)/s, gdy F(s) = α{f(t).

Twierdzenie o transformacie splotu (Borela). α{f(t)*g(t)} = F(s)G(s).

PARAMETRY FALOWE CZWÓRNIKA:

-impedancja falowa

-przekładnia impedancyjna

-przekładnia energetyczna

-współczynnik przenoszenia falowego g - tzw. Tamowalność

CHARAKTERYSTYKA ODKSZTAŁCENIA.

-Wartość średnia za okres funkcji f(t) definiuje zależność

-Wartość średnia z modułu funkcji

-Wartość skuteczna

- Współczynnik szczytu: Jest to stosunek wartości maksymalnej do skutecznej: s=A_max/A_sk; dla sinusoidy: A_sk=A_max/√2, s=√2; dla prostokąta: A_max=A; A_sk=A; s=1.

- Współczynnik kształtu: Jest to stosunek wartości skutecznej do wartości średniej z modułu: k=A_sk/A_śr; dla sinusoidy: A_śr = 2A_max/π; k = (A_max/√2)(π/2A_max) = 1,11; dla prostokąta: k = A/A = 1.

- Współczynnik zawartości harmonicznych: Jest to stosunek wartości skutecznej przebiegu po usunięciu z niego składowej stałej i pierwszej harmonicznej do wartości skutecznej przebiegu po usunięci z niego składowej stałej: dla sinusoidy: h=0; dla prostokąta: A₀=0; A_sk=A; h=0,43.

- Współczynnik odkształcenia: Jest to stosunek wartości skutecznej I harmonicznej do wartości skutecznej całego przebiegu: k₀ = A₁/A_sk; dla sinusoidy: k₀=A/A=1; dla prostokąta: k₀ = 4/π√2 = 0,9.

- Współczynnik zawartości k-tej harmonicznej: Jest to stosunek wartości skutecznych k-tej harmonicznej do I harmonicznej: h_k = A_k/A₁.

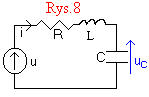
STAN NIEUSTALONY W SZEREGOWYM OBWODZIE RLC.

W celu sformułowania równania obwodu zastosujemy NPK: Ri + L(di/dt) + u_C = u, i podstawimy i=C(du_C/dt), otrzymując LC(d²u_CS/dt²) + RC(du_CS/dt) + u_CS = 0. Równanie to zapiszemy w postaci: (1) (d²u_CS/dt²) + 2α(du_CS/dt) + ω_n²uCS = 0, gdzie α=R/2L nosi nazwę stałej tłumienia, zaś ω_n = 1/√(LC) jest pulsacją drgań nietłumionych. Rozwiązanie równania (1) zależy od pierwiastków równania charakterystycznego s²+2αs+ω_n²=0, wynoszących: s_1,2 = -α ± √(α²-ω_n²). Rozróżniamy trzy przypadki:

1) α>ω_n, czyli R>2√(L/C) - pierwiastki równania charakterystycznego są rzeczywiste i ujemne, a ponadto s₁≠s₂. Rozwiązanie swobodne określa wzór: u_CS = A₁e^s1t+A₂e^s2t, zaś: i_S = C(dU_CS/dt) = C(A₁s₁e^s1t+A₂s₂e^s2t), przy czym A₁ i A₂ są stałymi zależnymi od warunków początkowych. Przebiegi mają charakter aperiodyczny i znikają od zera dla t→∞.

2) α=ω_n, czyli R=2√(L/C) - pierwiastki równania charakterystycznego są jednakowe, rzeczywiste i ujemne, a ponadto s₁ = s₂ = -α. Rozwiązanie jest następujące: u_CS = (A₁+A₂t)e^-αt, a zatem: i_S = C(dU_CS/dt) = C[A₂-α(A₁+A₂t)]e^-αt. Przebiegi aperiodyczne, graniczne, zanikające do zera dla t→∞.

3) α<ω_n, czyli R<2√(L/C) - pierwiastki równania charakterystycznego są zespolone, sprzężone s_1,2 = -α ± jω₀, gdzie ω₀ = √(ω_n²-α²) nosi nazwę pulsacji drgań własnych. Rozwiązanie równania ma postać: u_CS = Ae^-αtsin(ω₀t+ψ), gdzie A i ψ są stałymi. Stąd: i_S = C(dU_CS/dt) = CA[-αsin(ω₀t+ψ) + ω₀cos(ω₀t+ψ)]. Otrzymujemy ostatecznie: i_S = A√(L/C)e^-αtcos(ω₀t+ψ+η), przy czym: η = arctg(α/ω₀). Stopień tłumienia określa dekrement tłumienia ∂. Dla napięcia swobodnego u_CS otrzymujemy: ∂ = u_CS(t)/u_CS(t+T₀) = e^αTo, a stąd wynika następujący wzór na logarytmiczny dekrement tłumienia: ln∂ = αT₀.

TWIERDZENIA PRZEKSZTAŁCENIA LAPLACE'A:

Twierdzenie o liniowości. Jeżeli a i b są dowolnymi stałymi, to α{af(t)+bg(t)}= aF(s)+bG(s). Prawdziwość twierdzenia wynika bezpośrednio z faktu, że całkowanie jest operacją addytywną i jednorodną.

Twierdzenie o podobieństwie. Jeżeli a jest liczbą rzeczywistą dodatnią, to α{f(at)} = (1/a)F(s/a).

Twierdzenie o przesunięciu w dziedzinie zespolonej. Jeżeli k jest dowolną liczbą rzeczywistą lub zespoloną, to α{e^ktf(t)} = F(s-k). Twierdzenie to pokazuje jaki wpływ w dziedzinie przekształcenia Laplace'a ma pomnożenie funkcji f(t) przez czynnik e^kt.

Twierdzenie o opóźnieniu. Jeżeli h jest stałą rzeczywistą dodatnią, to α{f(t-h)u(t-h)} = e^-shF(s).

Twierdzenie o transformacie pochodnej. α{df/dt} = sF(s)-f(0), gdy F(s) = α{f(t).

Twierdzenie o transformacie całki. α{₀∫^t f(τ)dτ} = F(s)/s, gdy F(s) = α{f(t).

Twierdzenie o transformacie splotu (Borela). α{f(t)*g(t)} = F(s)G(s).

PARAMETRY FALOWE CZWÓRNIKA:

-impedancja falowa

-przekładnia impedancyjna

-przekładnia energetyczna

-współczynnik przenoszenia falowego g - tzw. Tamowalność

---