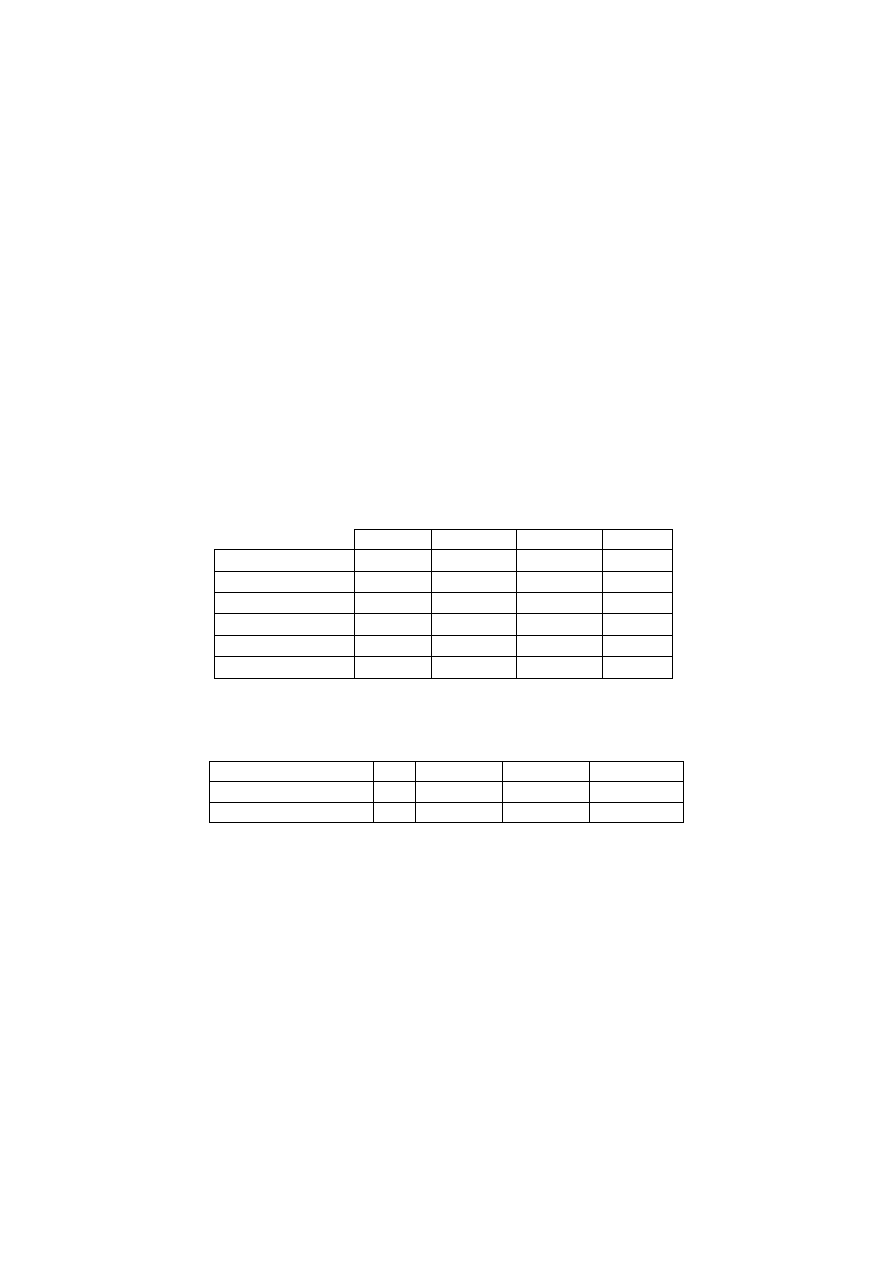
Egzamin ze statystyki, Studia Licencjackie Stacjonarne
TEMAT C – grupa 1
Czerwiec 2007
(imię, nazwisko, nr albumu)……………………………………………………………..
Przy rozwiązywaniu zadań, jeśli to konieczne, należy przyjąć poziom istotności 0,01 i
współczynnik ufności 0,95
Zadanie 1
Na zlecenie jednego z operatorów sieci telefonii komórkowej agencja badania rynku
„PENETRATOR” wykonała duże badanie konsumenckie, w którym zebrano informacje na
temat rynku telefonii komórkowej oraz zwyczajów i nawyków związanych z korzystaniem z
komórek. Badanie zostało zrealizowane na reprezentatywnej próbie 1000 gospodarstw
domowych, w których znajduje się, co najmniej jeden telefon komórkowy z abonamentem.
Poniższa tabela zawiera rozkład łączny (liczebności) wydatków na rachunki telefoniczne
względem miejsca zamieszkania:
wieś
małe miasta duże miasta razem
mniej niż 50 PLN
110
75
15
200
50-100
85
90
60
235
100-150
55
100
80
235
150-200
35
35
110
180
200-250
15
10
125
150
razem
300
310
390
1000
Dodatkowo jeden z pracowników agencji badania rynku obliczył podstawowe charakterystyki
wydatków względem miejsca zamieszkania:
wieś małe miasta duże miasta cała próba
ś
rednie
85,0
95,2
159,6
117,3
odchylenia standardowe 59,7
53,5
59,0
66,9
Korzystając z tabeli rozkładu oraz dodatkowych obliczeń proszę odpowiedzieć na następujące
pytania (odpowiedź uzasadnij):
a) (2 pkt) W której z trzech wyróżnionych klas miejsca zamieszkania, zróżnicowanie
wydatków na rachunki telefoniczne jest największe?
b) (2 pkt) Czy prawdą jest, że 50% gospodarstw domowych na wsi wydaje na rachunki
telefonicznie nie więcej niż 75 PLN, a 75% gospodarstw domowych w dużych miastach
nie więcej niż 200 PLN? Proszę obliczyć stosowne miary.
c) (3 pkt) Proszę dokonać estymacji punktowej (wraz z wartościami błędów) i przedziałowej
ś
rednich wydatków na rachunki telefoniczne w grupie wiejskich gospodarstw domowych.
d) (3 pkt) Czy można uznać, że rozkład wydatków na rachunki w całej badanej próbie jest
rozkładem normalnym? Zweryfikuj odpowiednią hipotezę, jeśli wiadomo, że statystyka
chi-2 przyjęła wartość 104. Jaka jest teoretyczna liczba gospodarstw domowych płacących
rachunki między 150 a 200 PLN?
Zadanie 2
Jako uzupełnienie badania zaprezentowanego w zadaniu 1, instytut badawczy postanowił
zanalizować zmiany liczby abonentów telefonii komórkowej w okresie 1996-2006 za pomocą
liniowej funkcji trendu (t=0,1,...,n). Zebrane dane (w milionach) charakteryzowały
następujące wartości:
- średnia liczba abonentów w badanym okresie (w milionach): 8,15
- odchylenie standardowe liczby abonentów: 5,1
- kowariancja: 16
- suma kwadratów reszt: 4,7
W oparciu to podane informacje proszę udzielić odpowiedzi na następujące pytania:
a) (3 pkt) Wyznacz i zinterpretuj parametry funkcji trendu (postać yˆ =at+b).
b)
(2 pkt) Wyznacz błędy oszacowań parametrów funkcji trendu.
c)
(2 pkt) Czy współczynnik trendu jest istotnie dodatni? Zweryfikuj odpowiednią hipotezę.
d)
(2 pkt) Wyznacz wartość współczynnika determinacji liniowej.
e)
(2 pkt) Podaj prognozowaną liczbę abonentów telefonii komórkowej w Polsce w roku
2010 wraz z błędem standardowym prognozy.
Zadanie 3
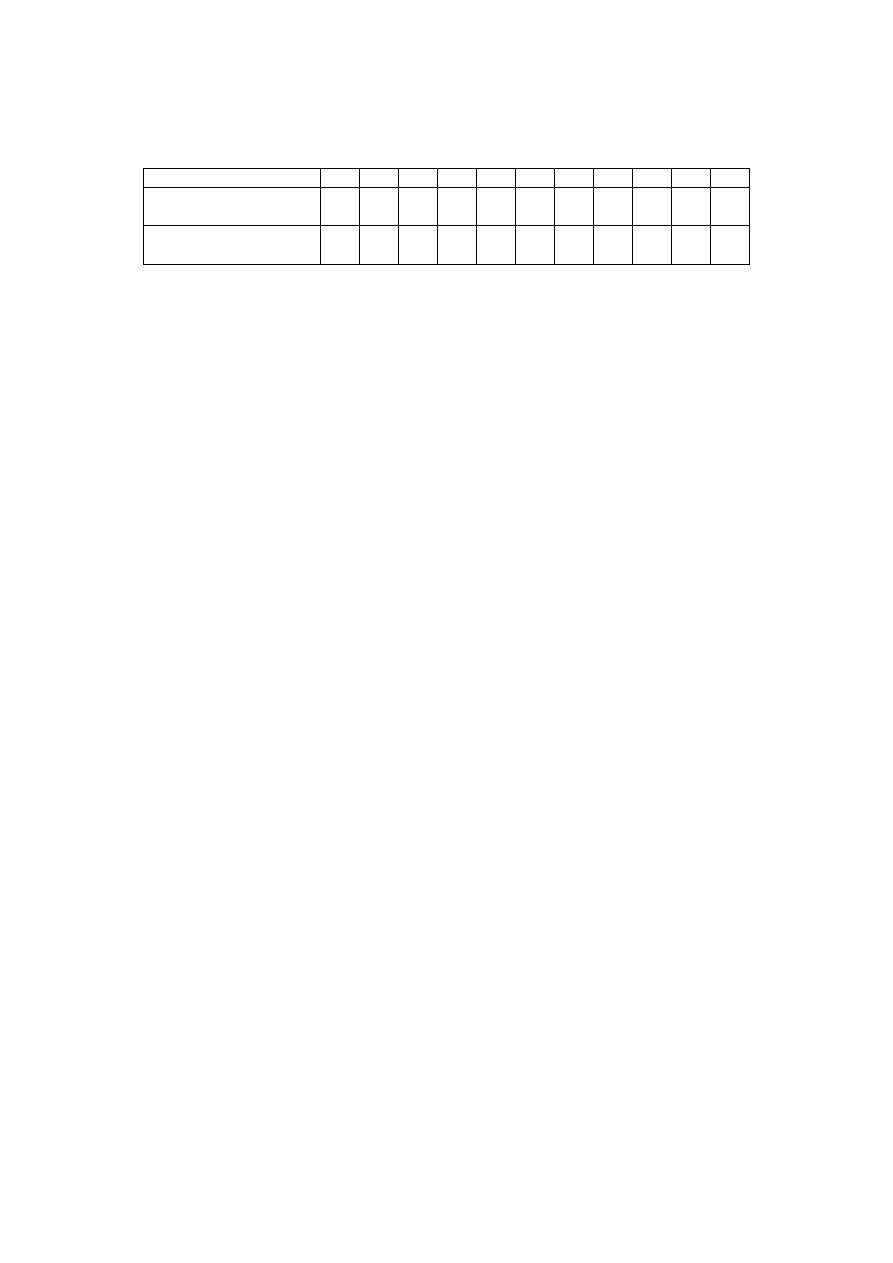
Poniższa tabela zawiera dane surowe wykorzystane w poprzednim zadaniu:
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006
liczba abonentów w
milionach
1,2 1,75 2,6 4,75 6,6
7
10 12,5 13,5 14
16
indeksy jednopodstawowe
1996=1,00
1
1,46 2,17 3,96 5,5 5,83 8,33 10,4 11,3 11,7 13,3
Dodatkowo zebrano informacje na temat dynamiki sprzedaży aparatów telefonicznych bez
abonamentu oraz telefonów na kartę (pre-paid) w dwóch kolejnych latach 2005 i 2006. W
roku 2005 wartość sprzedaży aparatów telefonicznych bez abonamentu wyniosła 5 mln PLN a
telefonów na kartę wyniosła 15 mln PLN. W 2006 łączna wartość sprzedaży wyniosła 18 mln
PLN. Wiadomo też, że cena telefonów bez abonamentu w 2006 w porównaniu z 2005 spadła
o 20% a cena aparatów na kartę o 5%.
W oparciu o zaprezentowane dane należy:
a)
(2 pkt) O ile procent zmieniła się liczba abonentów w roku 2006 w porównaniu do roku
2001?
b)
(2 pkt) Jak kształtowała się średnia dynamika liczby abonentów w latach 2001-2006?
c)
(3 pkt) Co miało większy wpływ na spadek łącznej wartości sprzedaży telefonów w roku
2006 w porównaniu do 2005, cena czy ilość?
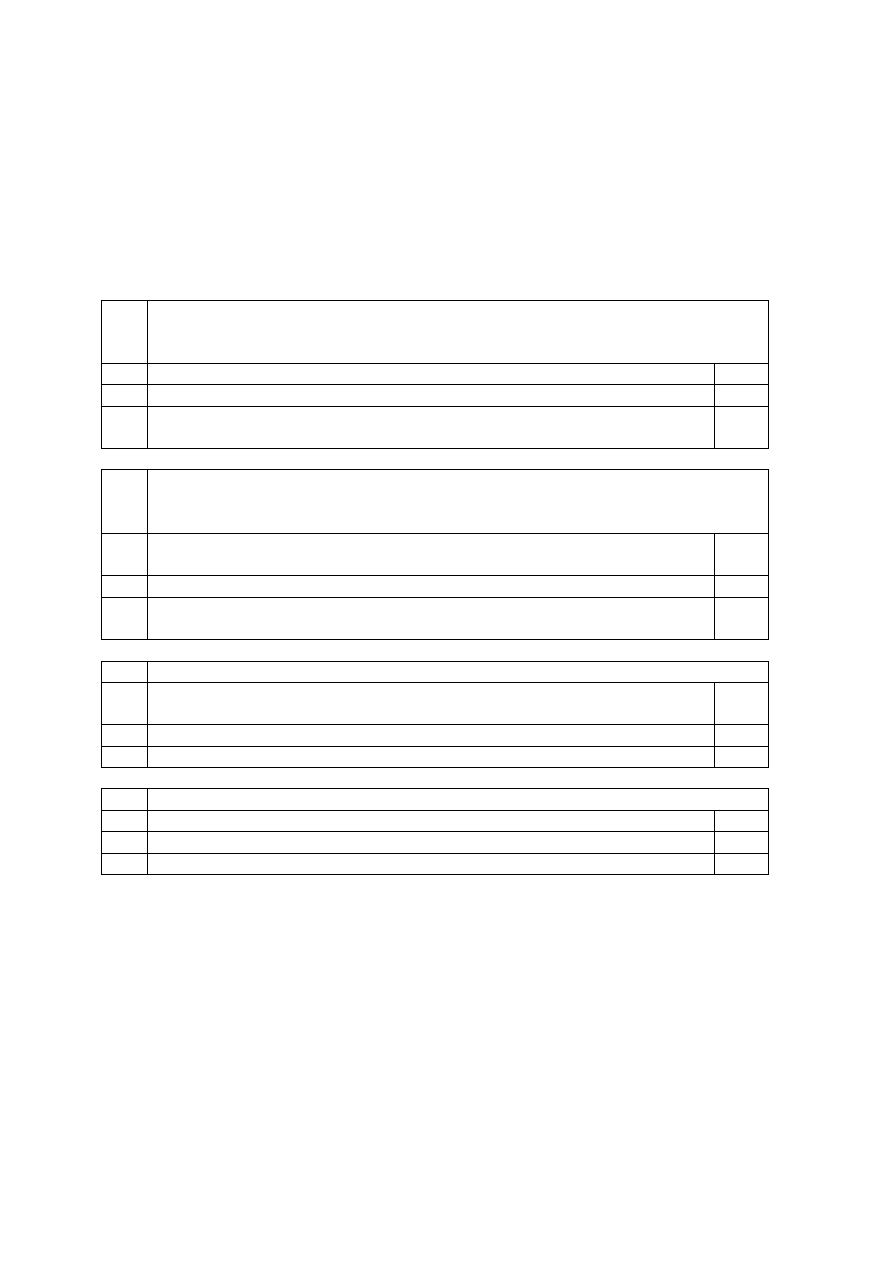
Zadanie 4 Część testowa
zaznaczyć w każdym przypadku odpowiedź
T-tak lub N-nie
Punktacja w zadaniu 4:
-
odpowiedź poprawna 1 pkt;
-
brak odpowiedzi 0 pkt;
-
odpowiedź błędna –1 pkt.
Jeżeli całkowita suma punktów z części testowej będzie ujemna, jako wynik części testowej zostanie
przyjęte 0 pkt.
1
Dane o miesięcznych zmianach realnego efektywnego kursu walutowego dla
Polski są zawarte w bazie danych Eurostat. W danych tych jako podstawę
porównań przyjmuje się styczeń 1999. Wynika z tego, że:
a
szereg czasowy jest szeregiem indeksów łańcuchowych
T N
b
szereg czasowy jest szeregiem indeksów jednopodstawowych
T N
c
indeksy te można przekształcić w indeksy łańcuchowe, dzieląc ich wartości
przez wartości poprzedzające
T N
2
Dystrybuanta rozkładu normalnego standardowego dla liczb ujemnych nie jest
stablicowana, a szukając odpowiednich wartości w tablicach, korzystamy z
właściwości Φ
Φ
Φ
Φ(-x) = 1 – Φ
Φ
Φ
Φ(x). Wynika ona m. in. z:
a
symetrii funkcji gęstości rozkładu normalnego standardowego względem osi
funkcyjnej
T N
b
faktu, że odchylenie standardowe w tym rozkładzie jest równe 1
T N
c
faktu, że pole pod całym wykresem funkcji gęstości tego rozkładu jest
równe 1
T N
3
Sformułowanie "dwustronny obszar krytyczny" oznacza, że:
a
obszar odrzuceń hipotezy zerowej jest sumą wartości dwóch zbiorów
rozdzielonych obszarem, dla którego H
0
nie odrzucimy
T N
b
hipoteza alternatywna może brzmieć: średnia w populacji jest mniejsza niż 5
T N
c
hipoteza alternatywna może brzmieć: średnia w populacji jest różna od 5
T N
4
Wartości spoza przedziału <0; 1> mogą przyjmować:
a
współczynnik korelacji liniowej Pearsona
T N
b
współczynnik zmienności
T N
c
dystrybuanta rozkładu normalnego
T N