Zadania z matematyki dla studentów I - go roku studiów stacjonarnych

na kierunku ekonomia

Zestaw 17

1. Na podstawie definicji pochodnej wyprowadzić wzór pochodnej funkcji:

a)
, b)
, c)
.

2. Ustalić wzór pochodnej funkcji:
,
.

3. Zbadać, czy funkcja
posiada pochodną w punkcie x = 0.

4. Dobrać wartości parametrów a i b tak, aby funkcja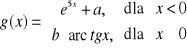
była ciągła i różniczkowalna dla każdego
.

5. Obliczyć pochodne funkcji:

,
,
,

,
,
,

,
,
,

,
,
,

,
,
,

,
,
.

6. Napisz równania stycznej do wykresu funkcji w podanym punkcie:

a)
w
, b)
w
.

7. Koszt produkcji x jednostek towaru jest dany wzorem
. Wyznaczyć funkcję opisującą koszt krańcowy. Jaki jest koszt krańcowy dla x = 100?

8. Wyznaczyć elastyczność funkcji:

a)
, b)
, c)
.

9. Funkcje opisujące wpływy i koszty dane są wzorami:

a)
,
; b)
,
.

Znaleźć funkcję opisującą zysk. Obliczyć elastyczność podanych funkcji dla
,
,
i zinterpretować otrzymane wyniki.

---