Ćwiczenie nr 8

Temat ćwiczenia: Pomiar długości fali świetlnej i stałej siatki dyfrakcyjnej.

Data wykonania ćwiczenia: 12.04.2007

Sekcja nr 3 w składzie:

1. TOPOREK Michał

2. TUROŃ Michał

Data oddania sprawozdania:

Ocena:

I. Wstęp teoretyczny

Dział optyki możemy podzielić na dwa poddziały: optykę geometryczną i optykę falową. O ile optyka geometryczna zaniedbuje skończone długości fali i przyjmuje, że światło rozchodzi się wzdłuż linii prostych, o tyle optyka falowa opiera się na falowej naturze światła. Dzięki optyce falowej możliwe jest wyjaśnienie takich zjawisk jak dyfrakcja, interferencja czy polaryzacja światła.

Dyfrakcja (inaczej ugięcie) to zmiana kierunku rozchodzenia się fal na krańcach przegrody; interferencja fal to nakładanie się fal koherentnych, a polaryzacja światła to zjawisko porządkowania fal.

Zjawisko dyfrakcji wyjaśnia tzw. Zasada Huygensa. Mówi ona, że każdy punkt, do którego dochodzą fale świetlne zachowuje się tak, jakby było w nim wtórne źródło wysyłające fale kulistą.

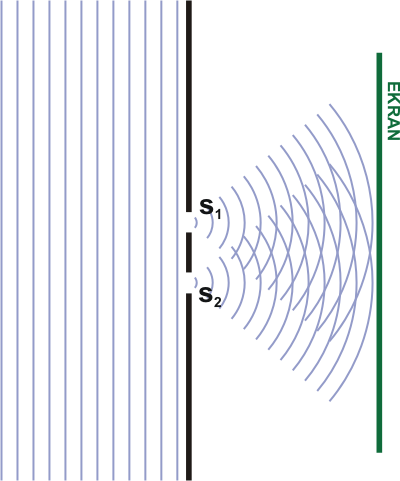
Zjawisko interferencji powstaje w wyniku nałożenie się dwóch lub więcej fal w danym punkcie przestrzeni. Prążkowy obraz interferencyjny możemy zaobserwować jednak tylko wtedy gdy źródła wysyłają fale jednakowej długości i fale wysyłane przez źródło zachowują w czasie stałą różnicę faz.

Zjawisko interferencji znalazło zastosowanie do wyznaczania długości fal świetlnych. W tym celu posługujemy się siatką dyfrakcyjną (zbiór równoległych i równo oddalonych szczelin wyciętych w nieprzezroczystej zasłonie).

Jeżeli na siatkę pada prostopadle wiązka promieni o długości fali λ, wtedy światło ugina się tak, że obrazy ugięcia mogą powstać tylko w określonych kierunkach - takich, dla których różnice dróg promieni wychodzących z dwóch sąsiednich szczelin równają się całkowitym wielkościom λ. Zachodzi wtedy związek:

gdzie to kąt ugięcia widm dyfrakcyjnych kolejnych rzędów, a d (tzw. stała siatki) jest odległością pomiędzy dwiema sąsiednimi szczelinami.

Jednak widać z powyższego wzoru, kąty pod którymi obserwuje się główne maksima nie zależą od liczby szczelin na siatce, natomiast zależą od długości fali światła padającego λ i odległości między szczelinami d.

Zjawiska dyfrakcji można wykorzystać do bardzo precyzyjnych pomiarów długości fali światła przy znanej wartości stałej siatki i odwrotnie.

II. Przebieg ćwiczenia

a) Pomiar długości fali światła.

Pomiędzy wiązką światła laserowego i ścianą ustawiono siatkę dyfrakcyjną o znanej stałej d. Następnie na papierze milimetrowym przypiętym do ściany zaznaczono jasne prążki kolejnych rzędów powstałych po interferencji światła i zmierzono odległości pomiedzy nimi. Na koncu wyznaczono długość fali światła laserowego wiedząc jaka jest odległość siatki dyfrakcyjnej od ściany.

b) Pomiar stałej siatki.

Zestawiono układ pomiarowy i postępowano dokładnie tak jak w pierwszym przypadku, z tym, że tym razem pomiędzy światło lasera i ścianę wstawiono siatkę dyfrakcyjną o nieznanej stałej d, którą zamierzano wyznaczyć znając już długość fali światła laserowego.

Tabele wyników:

d - stała siatki dyfrakcyjnej

l - odległość siatki dyfrakcyjnej od ekranu

a - odległość prążków kolejnych rzędów od prążka rzędu „0”

1. Pomiar długości fali światła.

d = 10

l = 30 cm

Rząd jasnego prążka	a [cm]
n = 1	2,2
n = 2	4,5
n = 3	6,7

sinα = a / √(a²+l²) (na podstawie twierdzenia Pitagorasa)

dla n=1 λ = ( 10µm * 0,073 )/ 1 = 0,73µm

dla n=2 λ = ( 10µm * 0,15 )/ 2 = 0,75µm

dla n=3 λ = ( 10µm * 0,22 )/ 3 = 0,73µm

λ_śr = 0,74µm

2. Pomiar stałej siatki.

λ = 0,74µm

l = 31 cm

Rząd jasnego prążka	a [cm]
n = 1	1,5
n = 2	3,1

sinα = a / √(a²+l²) (na podstawie twierdzenia Pitagorasa)

dla n=1 d = ( 1 * 0,74 )/ 0,05 = 14,8

dla n=2 d = ( 2 * 0,74 )/ 0,1 = 14,8

d_śr = 14,8

IV. Wnioski

Głównym powodem błędów powstałych po przeprowadzeniu doświadczenia były niedokładności związane z odczytem prążków interferencyjnych na ekranie. Doświadczenie prowadzone było w słoneczny dzień, a promienie słoneczne dodatkowo utrudniały odczyt. Ludzkie oko także nie jest doskonałe. Nawet o 1 mm błędnie odczytana odległość jasnego prążka n-tego rzędu od prążka zerowego rzędu powodowała znaczne różnice w otrzymanym wyniku. Na ekranie niektóre powstające prążki były rozmyte i nie wiadomo było jak zmierzyć odległość. Zaobserwowano również, że ustawienie lasera pod minimalnie innym kątem powodowało niewielkie zmiany w odległościach powstających prążków interferencyjnych. . Jeszcze jedną z przyczyn błędów może być fakt, że pomimo prostopadłego ustawienia siatki dyfrakcyjnej na stolikach otrzymane prążki nie były pionowe lecz lekko ukośne, co powodowało pewne niedokładności odczytu.

---