WIEiK Grupa 12	Szymon Łukasik	Zespół nr 9	Data wykonania: 11.05.2001
Nr ćwiczenia: 27	Dyfrakcja i interferencja światła lasera na szczelinach	Ocena:	Podpis:

1. Wprowadzenie

Dyfrakcja i interferencja fal świetlnych

Zjawisko dyfrakcji polega na uginaniu się promieni świetlnych padających na przeszkody lub przechodzących przez szczeliny. Efekty dyfrakcyjne są silne wówczas, gdy rozmiary obiektów znajdujących się na drodze fali świetlnej są porównywalne z jej długością λ. Jeśli za wąską szcze­liną o szerokości a, na którą pada fala świetlna o długości λ umieścimy ekran w odległości L » a (rys. poniżej), to będziemy na nim obserwować układ jasnych i ciemnych prążków o zmieniającym się natężeniu.

Położenie minimów natężenia światła możemy określić wg. wzoru:

a sinα_n = n λ [1]

n - rząd minimum

a - szerokość szczeliny

Interferencja fal polega na nakładaniu się dwu lub więcej fal harmonicz­nych o tej samej długości, prowadzącym do powstania ustalonego w czasie przestrzennego rozkładu obszarów wzmocnienia i osłabienia fali wypadkowej. Zjawisko to możemy obserwować, gdy światło pada na dwie szczeliny. Jeśli długość fali świetlnej λ jest większa od szerokości każdej ze szczelin to przecho­dzące przez nie i ugięte fale dają obraz interfe­rencyjny składający się na przemian z jasnych i ciemnych prążków o prawie jednakowym natężeniu (szkic poniżej przedstawia obraz interferencyjny otrzymany w wyniku padania światła lasera na 2 szczeliny - został on wykonany w trakcie ćwiczenia).

W określonym punkcie P ekranu obserwujemy prążek jasny, jeśli dociera do niego równocześnie maksimum (lub minimum) pierwszej i drugiej fali. Wówczas bowiem zachodzi sumowanie się amplitud fal wypadkowych. W przypadku, gdy w rozważanym punkcie P spotyka się minimum jednej i maksimum drugiej fali, dochodzi do wygaszenia fal.

Dla sytuacji przedstawionej na rys., gdzie r₁ i r₂ są odpowiednio odległo­ściami szczelin S₁ i S₂ od punktu P na ekranie, a δ = r₁ - r₂ jest tu różnicą dróg optycznych, warunkiem wzmocnienia jest, by δ była całkowitą wielokrotno­ścią długości fali λ

Przy założeniu, że odległość szczelin od ekranu L jest dużo większa niż odle­głość między szczelinami d (L»d), różnica dróg optycznych δ wyraża się wzorem:

Więc maksima w natężeniu światła występują wówczas, gdy:

[2]

gdzie n jest liczbą całkowitą.

Z kolei wygaszenia światła obserwujemy w tych punktach, dla których:

[3]

Światło wysyła­ne przez konwencjonalne źródła światła jest skomplikowaną superpozycją skończonych ciągów fal o różnych długościach, emitowanych przez atomy w sposób zupełnie przypadkowy. To sprawia, że przy nakładaniu się fal na siebie położenia obszarów wzmocnień i osłabień ulegają ciągłym zmianom i nie jest możliwe obserwowanie interferencji wiązek światła wysyłanych przez różne źródła. Mówimy, że są one wiązkami niespójnymi. Wyraźny, stabilny w czasie obraz interferencyjny możemy uzyskać tylko wtedy, gdy różnice faz między nakładającymi się falami są stałe w czasie obserwacji. Fale takie nazywamy spójnymi i źródłem ich są lasery.

Zasada działania lasera

Lasery są źródłami spójnego, monochromatycznego i w wysokim stopniu skolimowanego światła. Wiązka promieniowania laserowego powstaje w wy­niku zjawiska emisji wymuszonej promieniowania po uprzednim wytworzeniu w ośrodku czynnym stanu inwersji (odwrócenia) obsadzeń, polegającego na zwiększeniu liczby atomów wzbu­dzonych tak, by przewyższała liczbę atomów w stanie niższym. Proces ten określa się mianem pompowania.

Zależnie od materiału użytego jako ciało aktywne, dzielimy lasery na: kry­staliczne (rubinowy, neodymowy), gazowe (helowo-neonowy), lasery barwni­kowe (roztwory silnie fluoryzującego barwnika, np. rodaminy) i półprzewod­nikowe.

2. Metoda pomiaru, obliczenia i wyniki

a) wyznaczania szerokości szczeliny z obserwacji dyfrakcji światła

Oznaczając przez y odległość punktu P na ekranie od środka ekranu O - przyjętego w punkcie maksimum rzędu 0 - możemy napisać dla L>>a ,że różnica dróg optycznych jest równa:

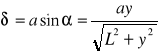
podstawiając ją do wzoru [1] otrzymujemy po przekształceniach wzór na szerokość szczeliny a jeżeli znamy położenie n-tego minimum (y_n) :

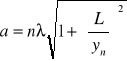
[4]

położenie minimów odczytujemy z wykresu zależności napięcia U, rejestrowanego przez fotodiodę od jej położenia y wzdłuż ekranu (jako punkt 0 przyjąłem punkt max. rzędu 0).

Oto uzyskane wyniki:

LP	y[mm]	U[V]
1	-22	0,09
2	-21	0,07
3	-20	0,06
4	-19	0,08
5	-18	0,12
6	-17	0,13
7	-16	0,10
8	-15	0,08
9	-14	0,14
10	-13	0,23
11	-12	0,25
12	-11	0,16
13	-10	0,15
14	-9	0,39
15	-8	0,65
16	-7	0,73
17	-6	0,51
18	-5	0,90
19	-4	3,10
20	-3	8,03
21	-2	12,36
22	-1	18,17
LP	y[mm]	U[V]
23	0	19,20
24	1	14,92
25	2	8,18
26	3	3,38
27	4	0,99
28	5	0,48
29	6	0,68
30	7	0,72
31	8	0,48
32	9	0,17
33	10	0,16
34	11	0,24
35	12	0,25
36	13	0,16
37	14	0,09
38	15	0,09
39	16	0,13
40	17	0,12
41	18	0,08
42	19	0,06
43	20	0,08

ILUSTRACJĘ WYNIKÓW STANOWI ZAŁĄCZONY WYKRES U(y).

Ze związku [4] wyliczamy szerokość szczeliny a dla każdego uzyskanego minimum - ponieważ uzyskane minima nie są symetrycznie rozłożone po obu stronach punktu 0 (dla 2 przypadków )wyliczam szerokość szczeliny dla minimów z obu stron punktu. Przyczyną takiej niedokładności jest najprawdopodobniej niedokładnie wyznaczony punkt 0 - maksimum rzędu 0.

Dodatkowe dane:

Odległość ekranu od źródła:	L=	1	m
Niepewność pomiarowa:	ΔL	0,0005	m
Długość fali świetlnej - laser półprzewodnikowy	λ=	6,70*10^-7	m
Niepewność przy określaniu położenia minimum yn	Δyn=	0,0005	m

A oto obliczone szerokości szczeliny:

Rząd minimum n	yn[mm]	yn[m]	a[m]
1	5	0,005	0,000134
1	-6	-0,006	0,000112
2	10	0,01	0,000134
2	-10	-0,01	0,000134
3	15	0,015	0,000134
3	-15	-0,015	0,000134
4	19	0,019	0,000141
4	-20	-0,02	0,000134
ŚREDNIA ARYTMETYCZNA a=			0,000132

Tak więc wyliczona szerokość szczeliny wynosi

• określamy błąd pomiarowy :

Dla małych kątów α - a z takimi mamy do czynienia w ćwiczeniu (y_n < 2,2 cm , a L=100 cm czyli L >> y_n) możemy skorzystać z zależności:

podstawiając ją do wzoru na minimum, wyliczając a dostajemy wyrażenie na błąd pomiarowy równe /korzystamy ze wzoru na niepewność iloczynu potęg wielkości prostych/:

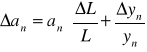
co daje niepewności maksymalne dla naszych pomiarów równe:

Rząd Minimum n	Niepewność Δan[m]	an[m]	Niepewność procentowa [%]
1	1,34*10^-^5	0,000134	10,05
1	9,25*10^-6	0,000112	8,28
2	6,77*10^-^6	0,000134	5,05
2	6,63*10^-^6	0,000134	4,95
3	4,53*10^-^6	0,000134	3,38
3	4,40*10^-6	0,000134	3,28
4	3,78*10^-6	0,000141	2,68
4	3,28*10^-^6	0,000134	2,45

Średnia niepewność maksymalna jednego pomiaru Δa = 6,51*10^-6m

Średnia niepewność procentowa jednego pomiaru σ_% = 4,93%

Ostatecznie obliczoną w wyniku doświadczenia szerokość szczeliny zapisujemy:

lub w mikrometrach:

b) wyznaczanie stałej siatki dyfrakcyjnej

Ponieważ warunkiem wystąpienia prążków jasnych jest spełnienie zależności:

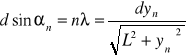
gdzie:

n - rząd widma

d - stała siatki /czyli odległość pomiędzy środkami sąsiednich szczelin/

L - odległość ekranu od siatki

y_n - odległość prążka n - tego rzędu od środka obrazu (za który przyjmuję prążek zerowy)

więc:

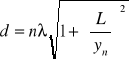
Oto wyniki pomiarów :

Rząd Maksimum n	yn[mm]	Rząd Maksimum n	yn[mm]
0	0	1	-9
1	10	2	-19
2	19	3	-29
3	29	4	-38
4	38

A oto wyliczone wartości d_n:

Rząd Maksimum n	yn[mm]	yn[m]	dn[m]
1	10	0,01	6,70E-05
1	-9	-0,009	7,44E-05
2	19	0,019	7,05E-05
2	-19	-0,019	7,05E-05
3	29	0,029	6,93E-05
3	-29	-0,029	6,93E-05
4	38	0,038	7,06E-05
4	-38	-0,038	7,06E-05

Średnia wartość

czyli na 1 centymetr przypada ok. 140 linii (dokładnie 142 wg. moich obliczeń).

• Rachunek błędu

Przy określaniu Δd stosujemy podobne założenie jak w części a) - ponieważ kąty w ćwiczeniu są małe więc:

więc błąd przy wyznaczaniu stałej siatki:

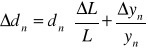
dla danych naszego ćwiczenia kształtuje się on tak jak podaje poniższa tabelka:

rz. Maksimum n	Δdn[m]	dn[m]	Niepewność procentowa [%]
1	3,38*10^-^6	6,70E-05	5,05
1	4,10*10^-^6	7,44E-05	5,51
2	1,89*10^-^6	7,05E-05	2,68
2	1,82*10^-^6	7,05E-05	2,58
3	1,23*10^-^6	6,93E-05	1,77
3	1,16*10^-^6	6,93E-05	1,67
4	9,64*10^-7	7,06E-05	1,37
4	8,93*10^-^7	7,06E-05	1,27

Średnia niepewność maksymalna jednego pomiaru Δd = 1,93*10^-6m

Średnia niepewność procentowa jednego pomiaru σ_% = 2,75%

Ostatecznie stałą siatki d obliczoną w trakcie ćwiczenia możemy zapisać :

c) obserwacja płaszczyzny polaryzacji światła laserowego

Umieszczając polaroid w wiązce laserowej badamy dla jakiego skręcenia płaszczyzny polaryzacji sygnał z fotodiody będzie najmniejszy, a dla jakiego największy). Ponieważ U~I (natężenie światła) więc wzór na stopień polaryzacji wiązki światła:

możemy zapisać

- wystarczy więc zmierzyć napięcie maksymalne i minimalne

Otrzymaliśmy:

U_MAX = 0,315 V // dla kąta 23⁰

U_MIN = 0,0035V // dla kąta 108⁰

Czyli po podstawieniu do wzoru na skręcenie płaszczyzny polaryzacji P otrzymujemy:

więc

P = 0,978

3. Wnioski

Niestety nie mogę porównać otrzymanych wyników z wartościami rzeczywistymi - można natomiast zauważyć, że jeśli dla szczeliny jej szerokość jest dosyć „racjonalna” ok. 0,1 mm to siatka dyfrakcyjna wg. moich obliczeń ma bardzo duże odległości między sąsiednimi szczelinami : dobre siatki mają ponad 1000 szczelin na 1mm - „nasza” siatka ma ok. 142 ale na cm !!! Jest to wynik nieco „podejrzany” jednakże nie zauważam w moich obliczeniach błędu więc trzeba się takowym rezultatem zadowolić.

Mimo tego „obliczeniowego” mankamentu ćwiczenie dostarczyło wiele ciekawych informacji na temat obrazów dyfrakcyjno-interferencyjnych uważam je więc za bardzo udane.

1

---