IV M B-inż.
Śliwa Sebastian; Dudziński Marcin; Szymanek Mariusz; Karpiński Rafał; Jendruszek Paweł; Masopust Krzysztof; Grzegorzek Marcin; Kuras Piotr; Recki Norbert.
Drgania skrętne wału silnika spalinowego tłokowego.
Wał korbowy silnika spalinowego tłokowego wraz ze sprzęgniętym z nim odbiornikiem mocy (śrubą okrętową lub prądnicą) i elementami układu korbowo-tłokowego tworzą układ drgający. Na taki układ oddziaływają okresowo zmienne momenty pochodzące od nacisku gazów. Momenty te mogą wywołać drgania skrętne, które w szczególnych warunkach rezonansu rzędów głównych mogą spowodować pęknięcie wału. Drgania skrętne takiego układu czyli układu rozpraszającego energię drgań, możliwe są tylko wtedy gdy na układ ten działa okresowo zmienny moment. Momentem wymuszającym drgania skrętne wału korbowego jest moment pochodzący od składowej stycznej siły tłokowej. Zmienność momentu siły stycznej jest taka sama jak siły stycznej Ps gdyż promień korby jest wielkością stałą. Jeśli stworzy się wykres siły stycznej to uzyska się jednocześnie wykres zmienności momentu obrotowego.
Moment obrotowy przedstawiony jako funkcja obrotu korby, zmienia się okresowo. Dla niezmiennego obciążenia i prędkości obrotowej silnika moment obrotowy zmienia się raz na obrót (co 2) w silniku dwusuwowym oraz raz na dwa obroty (co4) w silniku czterosuwowym. Moment obrotowy jest funkcją okresowo zmienną, ciągłą i określoną w każdym punkcie przedziału. Funkcję o podanych własnościach można zastąpić nieskończonym szeregiem trygonometrycznym, zwanym szeregiem Fouriera. Każdy składnik szeregu Fouriera jest prostą funkcją trygonometryczną (sin lub cos). Natomiast rozkład przebiegu funkcji na składowe nazywa się analizą harmoniczną albo harmonicznymi.
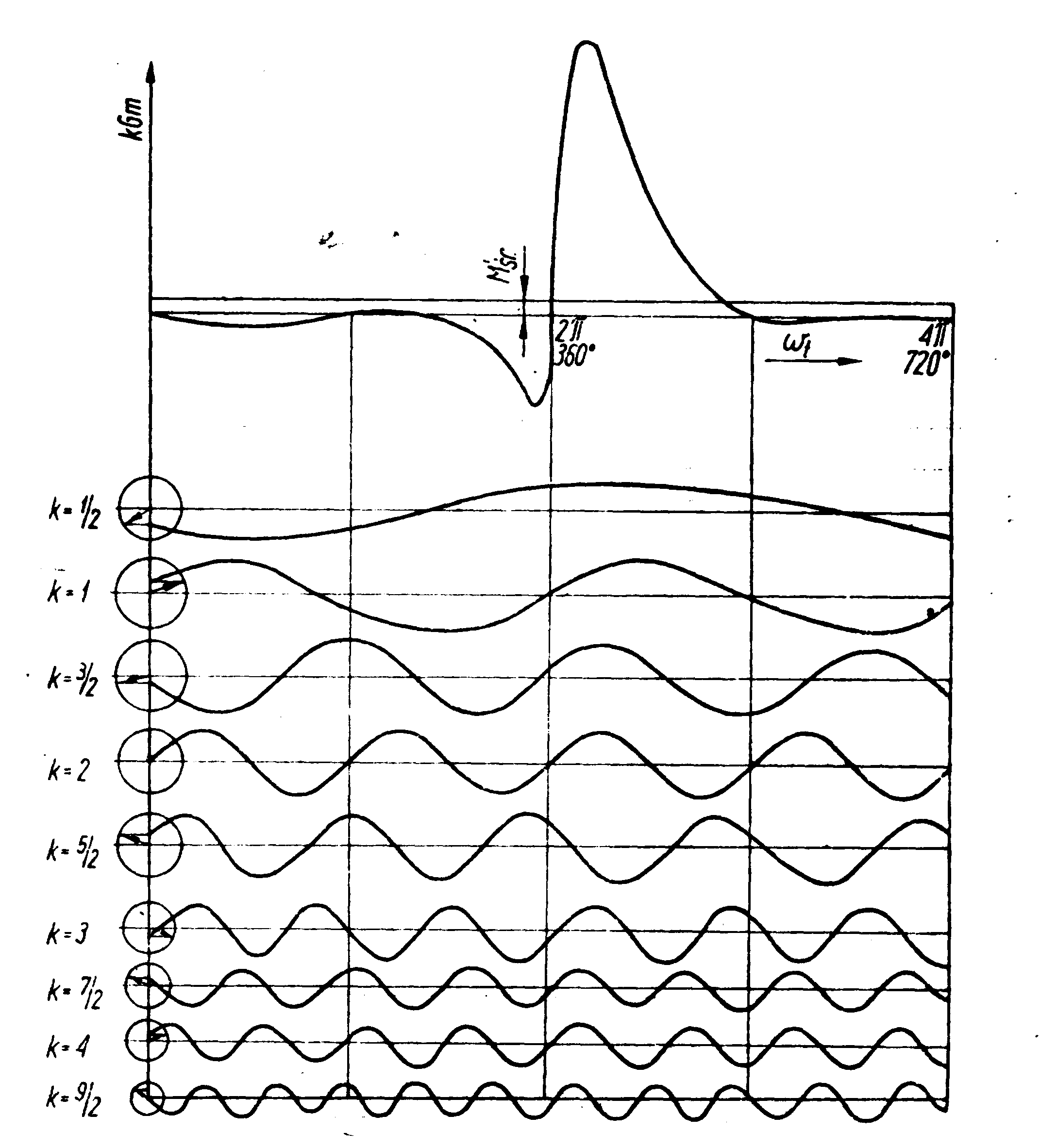
Przykład analizy harmonicznej wykresu momentu obrotowego jednocylindrowego silnika czterosuwowego pokazany jest na poniższym rysunku. Taki rozłożony moment obrotowy na z momentów składowych obrazuje działanie tychże okresowo zmiennych momentów tzn mogących wywołać drgania skrętne.
Drgania skrętne układu silnik-śruba mogą być szczególnie niebezpieczne w przypadku równej częstotliwości momentu wzbudzającego drgania i częstotliwość drgań własnych.
W rzeczywistości niektóre z możliwych rezonansów przypadają poza zakresem eksploatacyjnej prędkości obrotowej, dla innych zaś amplituda drgań rezonansowych jest tak mała, że drgania te nie mają żadnego praktycznego znaczenia. Tylko przy braku tłumienia amplituda drgań rezonansowych rośnie nieograniczenie nawet wtedy, gdy przyczyna wywołująca drgania jest nieskończenie mała. Podczas drgań układów rzeczywistych występuje zawsze tłumienie, to zna
czy rozpraszanie energii, kosztem której układ drga. W przypadku drgań układu silnik--śruba energia ta jest rozpraszana wskutek tarcia w łożyskach, tarcia tłoków i pierścieni cylindrach, oporu śruby napędowej oraz tarcia międzycząstkowego materiału wału korbowego i śrubowego.
Aby układ silnik śruba pobudzić do drgań, moment wymuszający drgania musi nie tylko zmieniać się z częstotliwością rezonansową, a1e praca tego momentu musi być większa od pracy sił tłumienia. Rezonansowe drgania występują tylko dla niektórych rzędów harmonicznych.
Ma to szczególne znaczenie w przypadku rozpędzania silnika oraz w przypadku obciążeń częściowych. Wynika to z faktu iż silnik w tym czasie przechodzi lub może pracować przy prędkości obrotowej równej rezonansowej. Dlatego też unika się takich stanów pracy i podczas rozpędzania silnika przechodzi przez te prędkości możliwie szybko.
Sześciocylindrowy silnik laboratoryjny Sulzer 6A20/24 został poddany badaniu dla różnych prędkości obrotowych, i obciążeń oraz przy zasymulowaniu awarii jaką było wyłączenie z pracy jednego cylindra. Urządzenie pomiarowe w postaci systemu czujek podłączonych do komputera zbierało dane o prędkości obrotowej, aktualnym momencie na wale oraz informację o drganiach skrętnych wału. Program komputerowy umożliwia zapis danych w charakterystycznych punktach wybranych przez użytkownika dla danej prędkości obrotowej i warunków (włączony i wyłączony z pracy jeden układ). Dodatkowo komputer na podstawie zebranych danych jest w stanie wygenerować widmo drgań skrętnych dla danych obrotów.
Tabela pomiarowa:
Pracują wszystkie cylindry |
Jeden cylinder wyłączony |
||||||
Obroty obr/min |
Amplituda [o] |
Moment [Nm] |
Naprężenie [MPa] |
Obroty obr/min |
Amplituda [o] |
Moment [Nm] |
Naprężenie [MPa] |
456 |
0,453 |
1112 |
26,400 |
449 |
0,706 |
1093 |
26,400 |
502 |
0,461 |
1342 |
26,632 |
502 |
0,622 |
1342 |
30,935 |
553 |
0,381 |
1557 |
24,211 |
552 |
0,528 |
1557 |
28,502 |
605 |
0,397 |
1810 |
24,714 |
596 |
0,458 |
1810 |
26,545 |
654 |
0,419 |
1995 |
25,390 |
604 |
0,467 |
1995 |
26,805 |
717 |
0,361 |
3137 |
23,567 |
678 |
0,467 |
2137 |
26,805 |
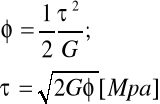
Na podstawie danych zebranych przez komputer o drganiach skrętnych wału na wyjściu z silnika można stosując poniższy wzór, obliczyć naprężenia w wale.
Gdzie:
G- moduł sprężystości poprzecznej (dla stali 769,3Mpa)
- naprężenie styczne
- kąt skręcenia w stopniach
Podstawione do tego wzoru dane dały wyniki zamieszczone w powyższej tabeli.
Mając dane naprężenie, moment skręcający oraz amplitudę skręcenia można stworzyć szereg charakterystyk dla silnika z pracującymi wszystkimi cylindrami oraz dla stanu awaryjnego w którym nie pracuje jeden układ.
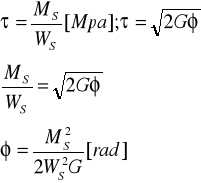
Znając moment skręcający oraz średnicę wału można wyznaczyć amplitudę rzeczywistą kąta skręcenia posługując się poniższym wzorem:
Gdzie:
Ms- moment skręcający
Ws- wskaźnik przekroju na skręcanie w miejscu mocowania tensometrów
W zamieszczonej poniżej tabeli znajduje się porównanie amplitud wyznaczonej z obliczeniową.
Pracują wszystkie cylindry |
Jeden cylinder wyłączony |
||||||
Obroty obr/min |
Amplituda [o] |
Amplituda Rzecz. [rad] |
Amplituda Rzecz. [o] |
Obroty obr/min |
Amplituda o] |
Amplituda Rzecz. [rad] |
Amplituda Rzecz. [o] |
456 |
0,453 |
0,795 |
0,014 |
449 |
0,706 |
0,768 |
0,014 |
502 |
0,461 |
1,158 |
0,020 |
502 |
0,622 |
1,158 |
0,020 |
553 |
0,381 |
1,559 |
0,027 |
552 |
0,528 |
1,559 |
0,027 |
605 |
0,397 |
2,107 |
0,037 |
596 |
0,458 |
2,107 |
0,037 |
654 |
0,419 |
2,559 |
0,045 |
604 |
0,467 |
2,559 |
0,045 |
717 |
0,361 |
6,328 |
0,110 |
678 |
0,467 |
2,936 |
0,110 |
Charakterystyki:
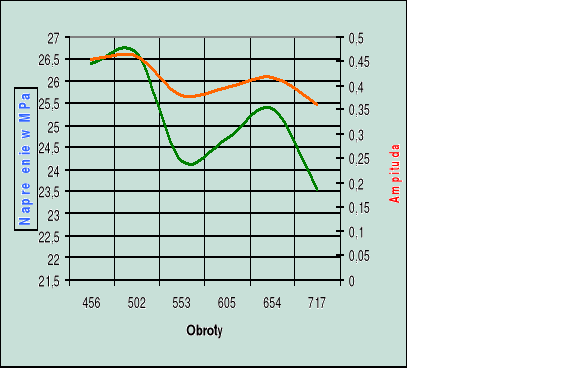
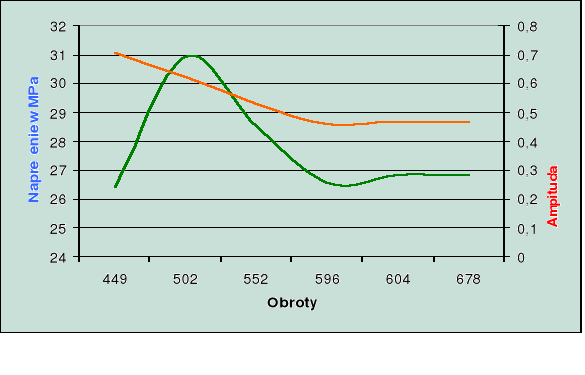
1. Naprężenie i amplituda w funkcji prędkości obrotowej:
pracują wszystkie cylindry
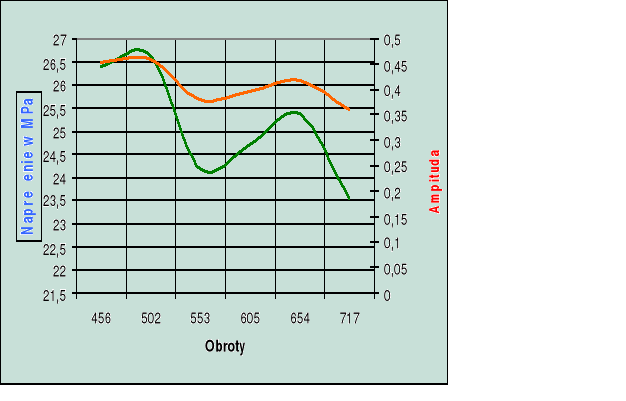
jeden cylinder nie pracuje
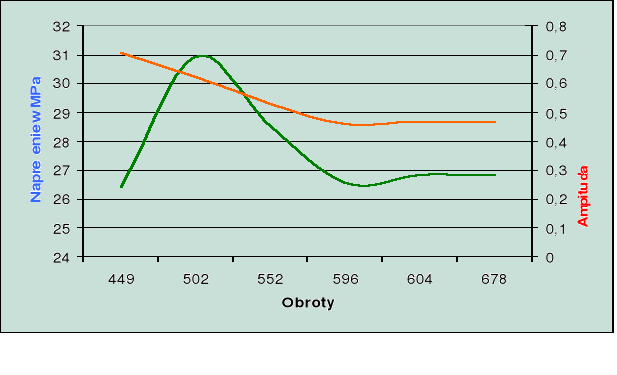
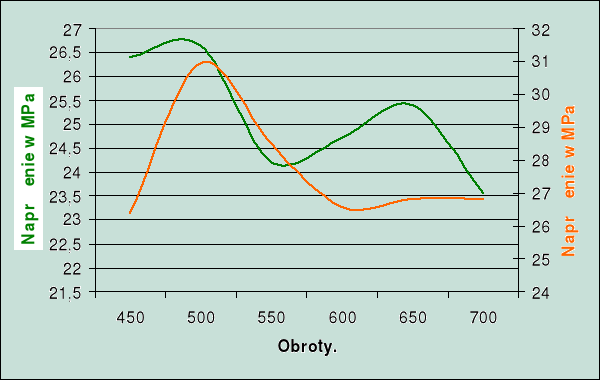
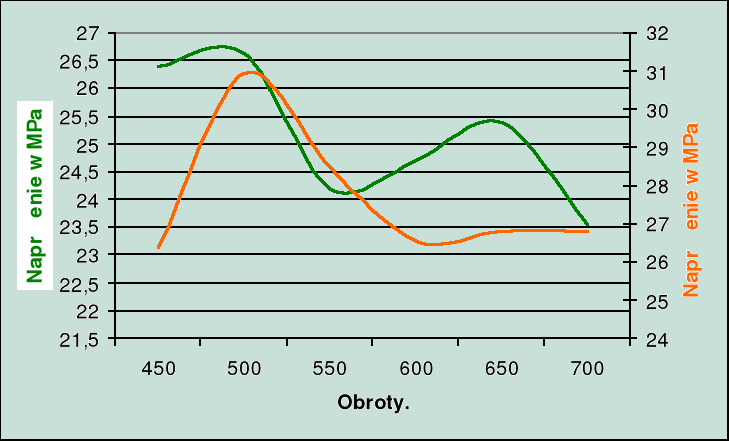
2. Wykresy porównawcze naprężeń.
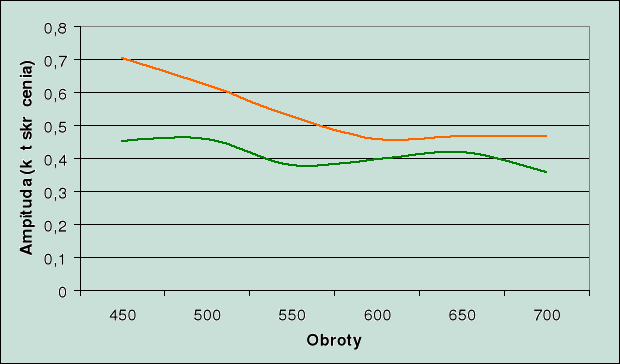
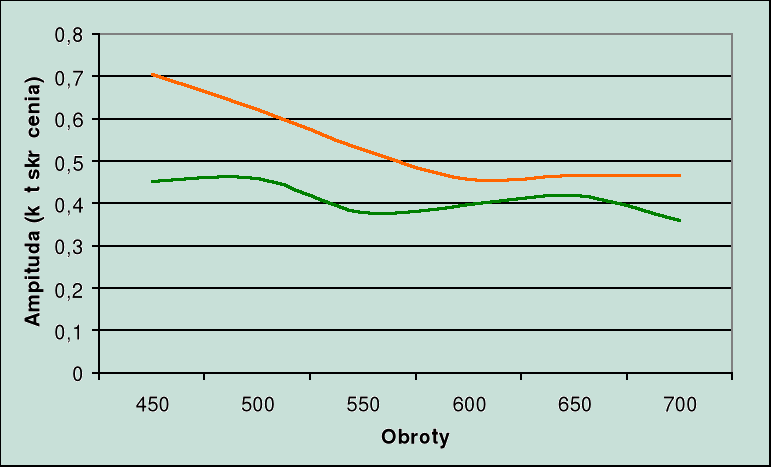
3. Wykres porównawczy amplitud.
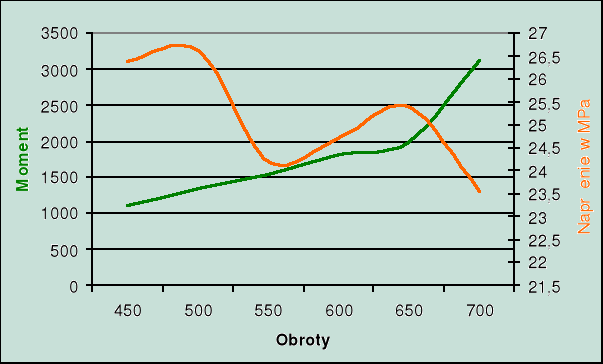
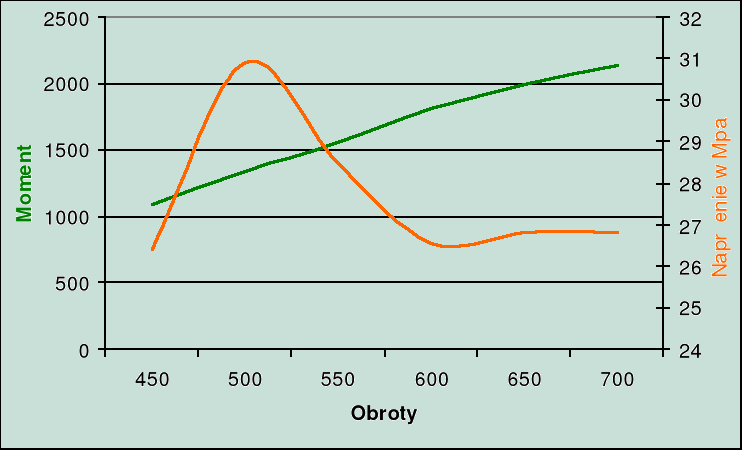
4. Wykres momentu i naprężenia.
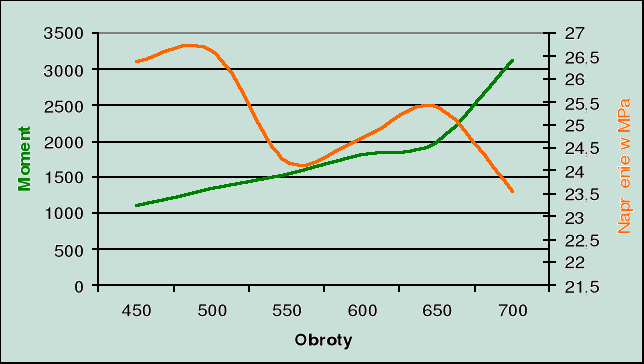
pracują wszystkie cylindry
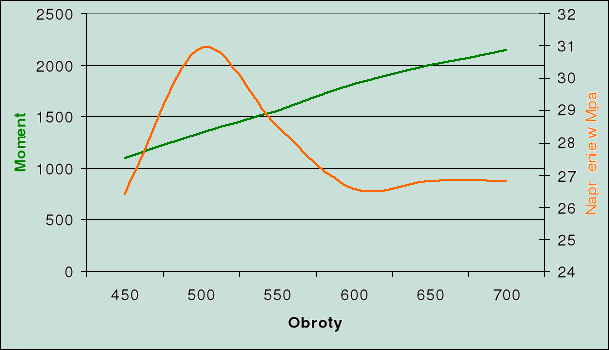
jeden cylinder nie pracuje
Na podstawie widma drgań skrętnych wygenerowanego przez komputer można określić częstotliwość i prędkość rezonansową która wynosi dla tego wydruku
f=5211 Hz i n=654obr/min.
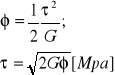
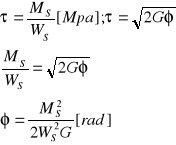
Wyszukiwarka
Podobne podstrony:
Silniki- drgania skretne walu, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, AM2, AKT
Metalock, Akademia Morska -materiały mechaniczne, Marcin, Technologia Remontów
Silnik asyn. pierścieniowy, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELE
silnik prądu stałego (tyrystor), Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola
silnik prądu stałego sterowany1, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola
Silnik asynchroniczny, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, ELEKTRA
Żmucki zaliczenie semestr zad3, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, SEMESTR
Silnik asynchroniczny-pierścieniwy lab1, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła
Silniki asynchroniczny klatkowy z autotransformatorm, Akademia Morska -materiały mechaniczne, szkoła
Żmucki zaliczenie semestr+, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, SEMESTR IV,
Pomiary płaskości podstawy silnika i współosiowości siedzeń, Akademia Morska -materiały mechaniczne,
Manewr ruszania z miejsca statku z silnikiem nienawrotnym i, Akademia Morska -materiały mechaniczne,
silniki zegarek, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, SEMESTR V, Trepowo
kadŁuby, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola1, III, SILNIKI
więcej podobnych podstron