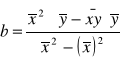Łukasz Grzeczkowicz
IwT gr Aa gr II
Badanie zależności metalu i półprzewodnika od temperatury
TEORIA:
Elektrony w paśmie przewodnictwa przemieszczają się swobodnie w całej objętości kryształu. W czasie tego chaotycznego ruchu ulegają one rozproszeniu na mechanicznych defektach sieci lub wywołanych drganiach. Średni czas między kolejnymi rozproszeniami nazywamy czasem relaksacji. Elektrony swobodne przemieszczają się w paśmie przewodnictwa w całej objętości kryształu z prędkością rzędu, pręd. Termiego.
Zakaz Pauliego mówi nam, że w atomie nie mogą istnieć dwa elektrony których stan kwantowy nie różnił by się przynajmniej jedną liczbą kwantową. Inaczej przy zbliżeniu N-atomów ich wyższe poziomy energetyczne łączą się we wspólne dla ciała kryształy pasm składające się z N blisko siebie położonych poziomów, z których każdy może zmieścić 2 elektrony o przeciwnych spinach i nazywamy pasmami energetycznymi, z których najwyższe jest pasmo walencyjne lub podstawowe a pasmo nad nimi to pasmo przewodnictwa. Pod względem przewodnictwa elektrony ciała dzielą się na: przewodniki, półprzewodniki oraz dialelektryki i izolatory (substancja nie posiada zapełnionych pasm energetycznych).
W temperaturze zera bezwzględnego dialelektryki i półprzewodniki są idealnymi izolatorami. Pod wpływem temperatury część elektronów (mała) może być przeniesiona z pasma walencyjnego do pasma przewodnictwa zgodnie z zależnością:
λ- Współczynnik temp. oporu
V0- Częstość rozproszeń wywołana defektami mech. lub atomami
V1- Częstość rozproszeń wywołana defektami cieplnymi obcymi
μ- Gęstość swobodna ładunków
Opór właściwy metali rośnie liniowo z temp.
R = Ro[1 + λ( T- To)]
Ro- opór w temperaturze równej 00C lub w temperaturze otoczenia
Oddzielną grupę przewodników stanowią stopy oporowe o składzie dobranym tak, że ich oporność Właściwa praktycznie nie ulega zmianie w szerokim zakresie temperatur.
Mostek Wheatsona- jeżeli badanym oporem jest R3=RX wówczas przy ustalonych oporach R1,R2 tak odbieramy opór R4, aby przez galwanometr nie popłynął prąd. Prąd nie będzie płynął jeżeli będzie spełnione:
I3R3 = I1R1 I3 = I4
I4R4 = I2R2 I1 = I2
z których otrzymujemy:
Jeżeli mamy opór R4 i znamy stosunek oporów R1 i R2 to wyznaczamy R3 czyli RX.
Opór w metalach zależy od częstości rozproszeń. Składa się ona z niezależnej od temp. częstości Vo wywołanej defektami mech. i atomami obcymi V1 wywołanej defektami cieplnymi.
Obliczenia:
|
|
Cu |
Termistor |
|||
T [0C] |
T [K] |
X=T-T0 [K] |
y=R [Ω] |
x'=1/T [K-1] |
R' [Ω] |
y'=ln(R') |
21 |
294 |
0 |
2380 |
0,0034 |
2600 |
7,863267 |
25 |
298 |
4 |
2380 |
0,0034 |
2100 |
7,649693 |
30 |
303 |
9 |
2410 |
0,0033 |
1760 |
7,473069 |
35 |
308 |
14 |
2440 |
0,0032 |
1410 |
7,251345 |
40 |
313 |
19 |
2480 |
0,0032 |
1120 |
7,021084 |
45 |
318 |
24 |
2520 |
0,0031 |
980 |
6,887553 |
50 |
323 |
29 |
2570 |
0,0031 |
810 |
6,697034 |
55 |
328 |
34 |
2600 |
0,0030 |
670 |
6,507278 |
60 |
333 |
39 |
2640 |
0,0030 |
550 |
6,309918 |
65 |
338 |
44 |
2690 |
0,0030 |
460 |
6,131226 |
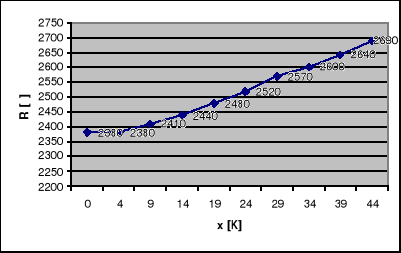
Wykres zależności oporu drutu miedzianego R od przyrostu temperatury x=T-T0.
Obliczenia :
Za pomocą regresji liniowej wyznaczam współczynnik temperatury oporu α.
![]()
![]()
gdzie
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
![]()
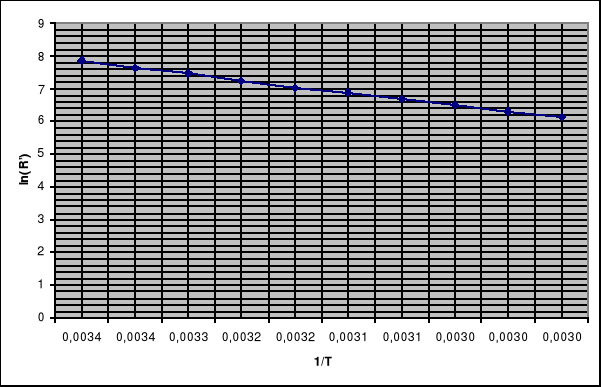
Stosując regresję liniową, wyznaczam szerokość przerwy energetycznej Eg termistora :
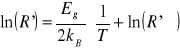
![]()
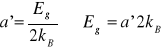
gdzie kB to stała Boltzmana
![]()
![]()
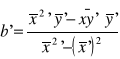
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3
Wyszukiwarka
Podobne podstrony:
4. Badanie drgań własnych metodą rezonansu, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria
wahadlo torsyjne, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria
wahadłorewersyjne, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria, Wyznaczanie przyspiesze
przyśpieszenie ziemskie, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria, Wyznaczanie przys
Wyznaczanie momentu bezwładności żyroskopu1, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratori
ABCDEF, Akademia Morska, semestr 1, Fizyka
cwicz 7, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria, Wyznaczanie stosunku CpCv
Podstawowa Teoria na Laboratoria Fizyki, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria, W
wahadłorewersyjne2, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratoria, Wyznaczanie przyspiesz
Dekrement tłumienia - Sprawozdanie - Bez obrazka, Akademia Morska, I semestr, FIZYKA, Fizyka - Labor
Ciepło topnienia i parowania - Sprawozdanie, Akademia Morska, I semestr, FIZYKA, Fizyka - Laboratori
badanie zaleźności temp oporu półprzewodnika, Politechnika Opolska, 2 semestr, Fizyka - Laboratorium
Zależność temperaturowa oporu półprzewodnika - 4, Politechnika Opolska, 2 semestr, Fizyka - Laborato
SprawozdanieTyrystor ppm, Akademia Morska, semestr 5, Półprzewodnikowe przyrządy mocy - LABORATORIUM
bibek spiral nie dla psa kielbasa, Akademia Morska, semestr 3, Projektowanie i konstrukcja Uządzeń (
cw07, Akademia Morska, 1 rok, Fizyka, FIZYKA1, fiza
Urządzenia nawigacyjne - Notatka do Kolokwium z wykładów, Akademia Morska, I semestr, urządzenia naw
więcej podobnych podstron