AGH, Wydział EAIiE |
Nazwisko i Imię: Feliksiak Jacek Szablowski Krzysztof |
|||
LABORATORIUM PODSTAW STEROWANIA LOGICZNEGO
|
|
|||
Rok akademicki : 2009/2010 |
Rok studiów: III Semestr: V |
|
||
Kierunek: Elektrotechnika
|
|
|||
Temat ćwiczenia: Dekoder 7-segmentowy |
||||
Data wykonania: 13.11.2009 |
Data oddania: 20.11.2009 |
Data zaliczenia sprawozdania:
|
||
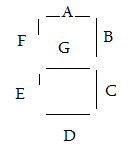
Dekoder jest podzielony na siedem segmentów tak jak na rysunku obok:
W celu obliczenia funkcji które nam umożliwią realizację logiczną dekodera 7-segmentowego. Należy każdemu z segmentów przypisać wartość 0 ( jak się ma nie świecić) albo 1 ( jeżeli ma się zaświecić) , w zależności od tego czy dany segment cyfry się świeci . Tak została stworzona poniższa tabelka dla wszystkich 7 segmentów:
cyfra |
x3 |
x2 |
x1 |
x0 |
a |
b |
c |
d |
e |
f |
g |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
5 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
6 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
7 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
8 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
10 |
1 |
0 |
1 |
0 |
- |
- |
- |
- |
- |
- |
- |
11 |
1 |
0 |
1 |
1 |
- |
- |
- |
- |
- |
- |
- |
12 |
1 |
1 |
0 |
0 |
- |
- |
- |
- |
- |
- |
- |
13 |
1 |
1 |
0 |
1 |
- |
- |
- |
- |
- |
- |
- |
14 |
1 |
1 |
1 |
0 |
- |
- |
- |
- |
- |
- |
- |
15 |
1 |
1 |
1 |
1 |
- |
- |
- |
- |
- |
- |
- |
Dla każdego z segmentów została stworzona tabela Karnough, z której można było wyliczyć funkcję potrzebne do stworzenia logicznych połączeń między przełącznikami. I tak dla segmentu:
A mamy:
B mamy:
C mamy:
D mamy:
E mamy:
F mamy:
G mamy:
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
1 |
0 |
1 |
1 |
01 |
0 |
1 |
1 |
1 |
11 |
- |
- |
- |
- |
10 |
1 |
1 |
- |
- |
![]()
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
1 |
1 |
1 |
1 |
01 |
1 |
0 |
1 |
0 |
11 |
- |
- |
- |
- |
10 |
1 |
1 |
- |
- |
![]()
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
1 |
1 |
1 |
0 |
01 |
1 |
1 |
1 |
1 |
11 |
- |
- |
- |
- |
10 |
1 |
1 |
- |
- |
![]()
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
1 |
0 |
1 |
1 |
01 |
0 |
1 |
0 |
1 |
11 |
- |
- |
- |
- |
10 |
1 |
1 |
- |
- |
![]()
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
1 |
0 |
0 |
1 |
01 |
0 |
0 |
0 |
1 |
11 |
- |
- |
- |
- |
10 |
1 |
0 |
- |
- |
![]()
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
1 |
0 |
0 |
0 |
01 |
1 |
1 |
0 |
1 |
11 |
- |
- |
- |
- |
10 |
1 |
1 |
- |
- |
![]()
X3X2 X1X0 |
00 |
01 |
11 |
10 |
00 |
0 |
0 |
1 |
1 |
01 |
1 |
1 |
1 |
1 |
11 |
- |
- |
- |
- |
10 |
1 |
1 |
- |
- |
![]()
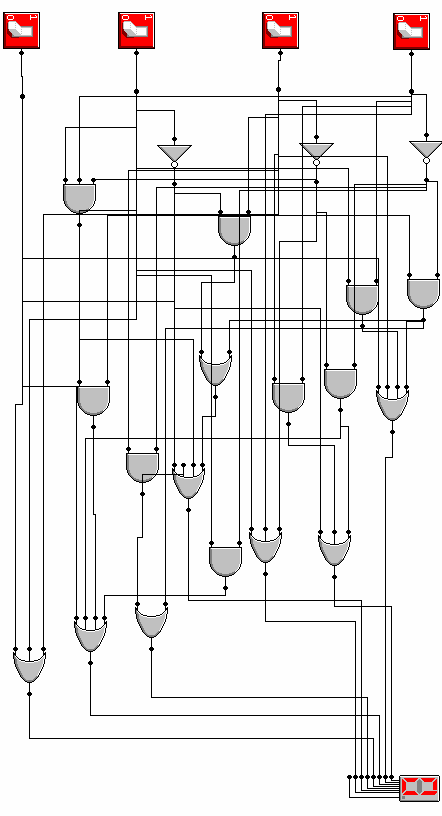
Po przedstawieniu funkcji F(a,b,c,d,e,f,g) w postaci bramek i odpowiednim połączeniu ich ze sobą oraz dekoderem powstał nam układ jak na rysunku :
Wyszukiwarka
Podobne podstrony:
El sprawko 5 id 157337 Nieznany
LabMN1 sprawko
INSTRUKCJA OBSŁUGI DEKODER SAGEM ISD 4285 PL
Obrobka cieplna laborka sprawko
Ściskanie sprawko 05 12 2014
1 Sprawko, Raport wytrzymałość 1b stal sila
stale, Elektrotechnika, dc pobierane, Podstawy Nauk o materialach, Przydatne, Sprawka
2LAB, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, Fizyka -
10.6 poprawione, semestr 4, chemia fizyczna, sprawka laborki, 10.6
PIII - teoria, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektro
grunty sprawko, Studia, Sem 4, Semestr 4 RŁ, gleba, sprawka i inne
SPRAWKO STANY NIEUSTALONE, Elektrotechnika, Elektrotechnika
SPRAWOZDANIE Z farmako, Farmacja, II rok farmacji, I semstr, fizyczna, Fizyczna, Sprawozdania z fizy
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
Zadanie koncowe, Studia PŁ, Ochrona Środowiska, Biochemia, laborki, sprawka
Piperyna sprawko PŁ, chemia produktów naturalnych, ćw. 5 PIPERYNA
03 - Pomiar twardości sposobem Brinella, MiBM Politechnika Poznanska, IV semestr, labolatorium wydym
Sprawozdanie nr 1 CECHY TECHNICZNE MATERIAfLOW BUDOWLANYCH, Budownictwo studia pł, sprawka maater
Sprawko badanie twardosci, Studia, WIP PW, I rok, MATERIAŁY METALOWE I CERAMICZNE, SPRAWOZDANIA
więcej podobnych podstron