Politechnika Krakowska |
|
rok: 1998/99 |
nr ćwiczenia |
Fizyka Techniczna |
MARCIN |
semestr: I |
42 |
Grupa: C |
KUK |
Ocena: |
Podpis: |
Zespół: 8 |
|
|
|
Pomiar współczynnika absorpcji promieni ![]()
emitowanych przez ![]()
w równowadze promieniotwórczej z ![]()
w glinie przy użyciu licznika Geigera - Műllera.
Teoria.
Promienie ![]()
pierwiastków radioaktywnych stanowią strumienie elektronów o prędkościach zmieniających się w sposób ciągły od 0 do pewnej wartości maksymalnej, charakterystycznej dla danego pierwiastka. Ich zdolność jonizacyjna i przenikliwość zależą od energii. Promienie o dużych energiach (do 3 Me V) tzw. twarde, przenikają przez blachy Al. grubości kilku milimetrów i warstwy powietrza grubości kilku metrów. Podczas przechodzenia przez materię cząstki ![]()
tracą energią na skutek oddziaływań z atomami absorbenta i zmieniają kierunek ruchu. Strumień elektronów rozprasza się i ulega absorpcji. Doświadczenia mówi, że wiązka równoległych promieni ![]()
o natężeniu ![]()
po przejściu warstwy substancji grubości ![]()
posiada natężenie ![]()
wyrażające się wzorem:
![]()
gdzie ![]()
nazywa się współczynnikiem absorpcji promieni ![]()
danego pierwiastka radioaktywnego dla badanej substancji, np. Al. Jednostką ![]()
jest ![]()
.
W naszym ćwiczeniu cząstki ![]()
powstają na skutek rozpadu kilku pierwiastków należących do szeregu promieniotwórczego uranu ![]()
(okres połowicznego rozpadu ![]()
lat).
Uran ![]()
wskutek emisji cząstek ![]()
przechodzi w ![]()
(UX, T=241 dni), który w dalszym ciągu emituje cząstki ![]()
oraz promienie ![]()
i przechodzi w ![]()
Pa (![]()
, T=1,14 min) również promieniotwórczy.
Pierwiastek ten emituje dwie grupy cząstek ![]()
o dwóch różnych energiach maksymalnych ( 2,31 Me V i 1,52 Me V), a zatem różnych współczynnikach absorpcji, jednak cząstki o dużej energii (2,31 Me V) stanowią ułamek procentu całego promieniowania ![]()
. Również pozostałe grupy promieni ![]()
pochodzące od dalszych członów szeregu uranowego, jakkolwiek występujące w większych ilościach, nie wpływają na wyniki pomiaru, ponieważ są tak „miękkie”, że zostają zaabsorbowane przez płytki Al. o grubości około 0,1 mm.
W celu wyznaczenia ![]()
przykrywamy źródło promieni ![]()
(warstewkę ciała radioaktywnego) kolejno płytkami blachy aluminiowej o różnych grubościach x i mierzymy liczbę cząstek ![]()
przechodzących w minucie przez płytkę. Pisząc równanie ![]()
dla warstw o grubościach ![]()
i ![]()
i logarytmując je stronami, mamy:
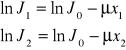
stąd:
![]()
Postępowanie dokładniejsze polega na mierzeniu natężeń przy stopniowo wzrastającej grubości absorbenta i sporządzeniu wykresu ilJ jako funkji x. Wykres ten, jak widać z równania :
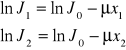
powinien być linią prostą. Obieramy na prostej 2 dostatecznie odległe punkty i wstawiając do:
![]()
dane odczytane z wykresu, obliczamy ![]()
. Wykres lnJ=f(x) odbiega od prostej w przypadku, gdy promieniowanie ![]()
pierwiastka jest mieszaniną 2 lub więcej grup promieni znacznie różniących się współczynnikiem absorpcji.
Przystępując do pomiarów licznikowych należy zwrócić uwagę na następujące okoliczności: rozkład w czasie cząstek jonizujących, wpadających do licznika, jest przypadkowy. Jeżeli 2 cząstki wpadają po sobie w odstępie czasu krótszym od „czasu martwego” licznika, wówczas są policzalne jako jedna. Ilość takich pominiętych cząstek rośnie wraz z ilością cząstek wpadających w jednostce czasu. Rzeczywista ilość wpadających cząstek jest większa od wskazań przelicznika. Przyjmiemy jednak, że przy przeliczniku elektronowym i zliczeniach kilkuset cząstek na minutę błąd ten jest do pominięcia.
Przed rozpoczęciem pomiarów należy też ustalić z jakim błędem chcemy wielkość mierzoną uzyskać. Według teorii prawdopodobieństwa błąd średni ![]()
obserwowanej ilości N zdarzeń przypadkowych wynosi:
![]()
Błąd procentowy: ![]()
. Jeżeli chcemy znać N z dokładnością np. 5%, to musimy obserwować około 400 impulsów, jeżeli z dokładnością 1% - już 10 000. Jeżeli licznik przy danym natężeniu promieniowania liczy np. 50 impulsów na minutę, to obserwacja w I przypadku musi trwać ![]()
minut, w II ![]()
minut. Błąd średni sumy lub różnicy wyników dwóch pomiarów ![]()
i ![]()
wynosi:
![]()
.
W celu pomiaru liczby cząstek jonizujących, wpadających do licznika w 1 minucie postępujemy następująco:
Wyznaczamy tzw. tło licznika, tj. liczbę cząstek zliczonych w jednej minucie bez preparatu radioaktywnego; pochodzą one od zanieczyszczeń radioaktywnych w otoczeniu i w materiale licznika, od promieniowania kosmicznego i innych przyczyn.
Wyznaczamy liczbę zliczeń
w obecności preparatu radioaktywnego, przysłoniętego płytką absorbującą o danej grubości x.Ponieważ nasz preparat prócz cząstek
wysyła jeszcze dość przenikliwe promieniowanie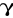
, na które licznik reaguje, chociaż z małą wydajnością, należy uwzględnić udział tego promieniowania w rejestrowanych impulsach, chociażby w sposób przybliżony. Przysłąniamy w tym celu źródło płytką aluminiową grubości 3-4 mm, tak by wszystkie cząstki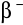
były zaabsorbowane, a pozostały tylko promienie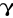
. Stwierdzamy to w ten sposób, że dokładanie dalszych 1-2 mm Al. nie zmienia ilości zliczeń w minucie. Cząstki rejestrowane obecnie pochodzą od „tła” i promieni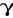
. Oznaczamy ich ilość łączną w minucie przez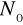
.Różnica
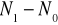
podaje liczbę cząstek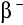
zarejestrowanych w minucie przez licznik
Doświadczenie.
Błąd systematyczny grubości absorbera ![]()
.
Błąd średni ![]()
różnicy dwóch pomiarów wynosi ![]()
Opracowanie wyników pomiaru wielkości zależnych liniowo.
![]()
![]()
Współczynniki: a, b obliczamy posługując się metodą regresji liniowej.
n- liczba pomiarów
Lp. |
|
|
|
|
|
1 |
3,416662232 |
55,16815127 |
0,2116 |
7,427526592 |
0,46 |
2 |
3,857504723 |
51,98827037 |
0,286225 |
7,210289201 |
0,535 |
3 |
4,359337746 |
51,07182365 |
0,3721 |
7,146455321 |
0,61 |
4 |
6,670117561 |
38,85969803 |
1,1449 |
6,23375473 |
1,07 |
5 |
8,045678372 |
27,653014 |
2,3409 |
5,258613315 |
1,53 |
6 |
8,278320744 |
26,76976341 |
2,56 |
5,173950465 |
1,6 |
7 |
8,140803973 |
23,62136398 |
2,805625 |
4,860181476 |
1,675 |
8 |
8,298670291 |
22,48748689 |
3,0625 |
4,742097309 |
1,75 |
9 |
8,198059837 |
13,76060791 |
4,8841 |
3,709529338 |
2,21 |
10 |
7,48322153 |
7,855153595 |
7,1289 |
2,802704693 |
2,67 |
Suma |
66,74837701 |
319,2353331 |
24,79685 |
54,56510244 |
14,11 |
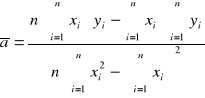
![]()
![]()
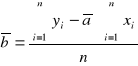
![]()
![]()
![]()
![]()
Po obliczeniu parametrów a i b prostej należy obliczyć ich odchylenie standardowe Sa i Sb.
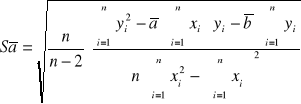
![]()
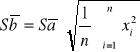
![]()
Lp. |
Grub. kol. płyt. Absorb. [mm] |
Grubość absorb. [mm] |
Czas obs. |
N |
N (1 min.) |
N-N0 |
ln(N-N0) |
|
|
N0 |
3,68 |
|
02:00,0 |
580 |
290 |
|
|
|
|
tło |
Tło |
|
14:59,9 |
1977 |
132 |
|
|
|
|
|
Glin |
|
|
|
|
|
|
|
|
1 |
0,46 |
0,46 |
01:59,9 |
3940 |
1972 |
1682 |
7,43 |
47,56 |
0,03 |
2 |
0,075 |
0,535 |
02:00,6 |
3303 |
1643 |
1353 |
7,21 |
43,97 |
0,03 |
3 |
0,075 |
0,61 |
01:59,3 |
3101 |
1560 |
1270 |
7,15 |
43,01 |
0,03 |
4 |
0,46 |
1,07 |
01:59,6 |
1594 |
800 |
510 |
6,23 |
33,01 |
0,06 |
5 |
0,46 |
1,53 |
01:59,2 |
958 |
482 |
192 |
5,26 |
27,79 |
0,14 |
6 |
0,07 |
1,6 |
02:00,1 |
934 |
467 |
177 |
5,17 |
27,51 |
0,16 |
7 |
0,075 |
1,675 |
01:59,7 |
836 |
419 |
129 |
4,86 |
26,63 |
0,21 |
8 |
0,075 |
1,75 |
01:59,8 |
808 |
405 |
115 |
4,74 |
26,36 |
0,23 |
9 |
0,46 |
2,21 |
02:00,1 |
662 |
331 |
41 |
3,71 |
24,92 |
0,61 |
10 |
0,46 |
2,67 |
02:00,2 |
614 |
306 |
16 |
2,80 |
24,42 |
1,48 |
Miedź |
|
|
|
|
|
|
|
|
|
1 |
0,06 |
0,06 |
02:00,1 |
4839 |
2417 |
2127 |
7,66 |
52,03 |
0,02 |
2 |
0,06 |
0,12 |
02:00,0 |
3191 |
1596 |
1306 |
7,17 |
43,43 |
0,03 |
3 |
0,06 |
0,18 |
01:59,3 |
2234 |
1124 |
834 |
6,73 |
37,60 |
0,05 |
4 |
0,06 |
0,24 |
01:59,9 |
1692 |
847 |
557 |
6,32 |
33,72 |
0,06 |
5 |
0,06 |
0,3 |
01:59,9 |
1258 |
630 |
340 |
5,83 |
30,33 |
0,09 |
6 |
0,06 |
0,36 |
01:59,3 |
1048 |
527 |
237 |
5,47 |
28,58 |
0,12 |
7 |
0,06 |
0,42 |
02:00,1 |
838 |
419 |
129 |
4,86 |
26,62 |
0,21 |
8 |
0,06 |
0,48 |
02:00,1 |
732 |
366 |
76 |
4,33 |
25,61 |
0,34 |
9 |
0,06 |
0,54 |
02:00,9 |
700 |
347 |
57 |
4,05 |
25,24 |
0,44 |
10 |
0,06 |
0,6 |
02:00,1 |
680 |
340 |
50 |
3,91 |
25,09 |
0,50 |
Wyliczenie współczynnika absorpcji pierwszego materiału:
![]()
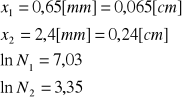
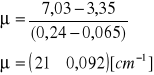
Współczynnik absorpcji w przybliżeniu odpowiada współczynnikowi glinu. (Tab. 17[cm-1])
Wyliczenie współczynnika absorpcji drugiego materiału:
![]()
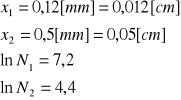
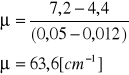
Współczynnik absorpcji w przybliżeniu odpowiada współczynnikowi miedzi i mosiądzu. (Tab. 56[cm-1])
Wyznaczenie prostokątów niepewności pomiarowej.
![]()
Błąd systematyczny: Δx=0,005[mm]
Wnioski:
Błędy występujące w doświadczeniu spowodowane są przede wszystkim przez brak zitegrowania licznika z czasomierzem. Wyniki tabicowe współczynnika absorbcji dla glinu i miedzi nie mieszczą się w przedziale wyliczeń.
1
5
Wyszukiwarka
Podobne podstrony:
40 Bernady (2), Mieszanka WIŚ, Fizyka Wiś Iś
40 Balawender (2), Mieszanka WIŚ, Fizyka Wiś Iś
33 Bernady 1, Mieszanka WIŚ, Fizyka Wiś Iś
14B (2), Mieszanka WIŚ, Fizyka Wiś Iś
25 Bernady, Mieszanka WIŚ, Fizyka Wiś Iś
opracowanie34 (2), Mieszanka WIŚ, Fizyka Wiś Iś
53 Karpinska (2), Mieszanka WIŚ, Fizyka Wiś Iś
tabelka (2), Mieszanka WIŚ, Fizyka Wiś Iś
33 Bernady 2, Mieszanka WIŚ, Fizyka Wiś Iś
11, Mieszanka WIŚ, Fizyka Wiś Iś
więcej podobnych podstron