Dynamika relatywistyczna

• Dodawanie prędkości według Einsteina:

Transformacje Lorentza:

i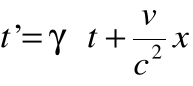

Różniczkując wyrażenia na te współrzędne czasoprzestrzeni:

i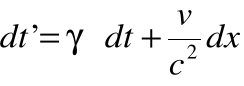

i dzieląc je przez siebie, otrzymamy:

gdzie:

Jest to wzór Einsteina na dodawanie prędkości.

• Dla
mamy:
bez względu na
!

Pęd relatywistyczny

• Klasyczna definicja pędu:

Taka definicja pędu, w połączeniu z transformacją Einsteina dla prędkości nie zapewni nam jednak spełnienia zasady zachowania pędu! (
jest prędkością cząstki).

• Nowa definicja pędu (która zapewni prawdziwość zasady zachowania pędu przy transformacji do dowolnego układu współrzędnych) podana przez Einsteina:

gdzie: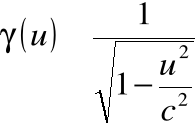

(uwaga! Podobieństwo oznaczeń, ale TO
zależy od prędkości cząstki
, a nie od prędkości
poruszania się układu współrzędnych!).

Pęd relatywistyczny - c.d.

• Dla tak zdefiniowanego pędu, możemy podać również zasady transformacji przy zmianie układu współrzędnych:

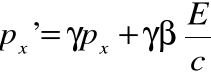
i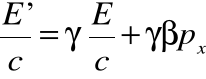

gdzie:
i

• Wielkości
i
transformują się podobnie jak para:
i
!

• Wielkość
oznacza składową pędu w kierunku prędkości „transformującej” z jednego układu współrzędnych do drugiego. Einstein utożsamił wielkość
z energią cząstki zakładając, że wielkości pędu i energii powinny się zachowywać względem siebie jak położenie i czas.

Energia relatywistyczna

• Podana definicja pędu w przypadku prędkości dużo mniejszych od prędkości światła przechodzi w definicję klasyczną:

• Energia zdefiniowana przez Einsteina też powinna ulec takiej transformacji, a więc:

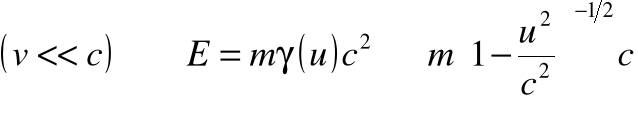
• Dla małych prędkości możemy jeszcze skorzystać z rozwinięcia w szereg wyrażenia na energię. Otrzymamy wtedy:

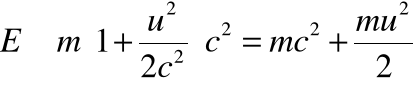
Energia relatywistyczna - c.d.

• Przypomnijmy wzór na rozwinięcie „nowej” definicji energii:

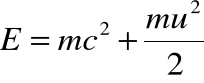
• Drugi człon jest klasyczną energią kinetyczną - energią cząstki swobodnej o prędkości
. Pierwszy człon jest natomiast pewną stałą, którą według praw mechaniki klasycznej można dodać jako dowolną wartość do całkowitej energii ciała (por. pojęcie energii potencjalnej!).

• Według Einsteina ten drugi człon:

ma sens energii spoczynkowej ciała - wielkości, której istnieniu zawdzięczamy m.in. bombę atomową...

Zasady zachowania pędu i energii

• Pokażemy, że tak zdefiniowane pęd i energia spełniają zasady zachowania przy transformacji układu współrzędnych.

Rozważmy układ
oddziałujących cząstek. Początkowe wartości całkowitego pędu (dla uproszczenia: bez indeksu „x”) i energii (małe litery oznaczają wielkości „początkowe”):

i

Transformacje Einsteina dla poszczególnych składowych:

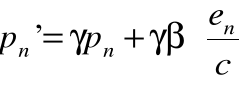
i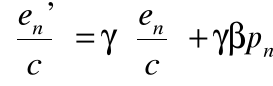

Zakładamy, że całkowite wielkości pędu i energii są zachowane (duże litery oznaczają wielkości „końcowe”):

i

Zasady zachowania pędu i energii - c.d.

• Dodając wartości pędów poszczególnych cząstek:

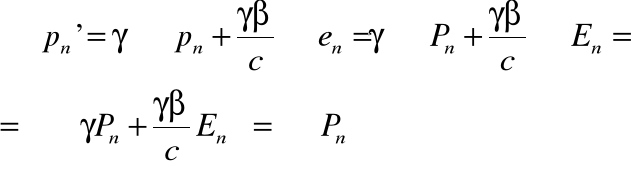
• Podobny wynik otrzymamy dla energii:

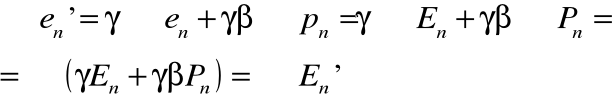
• A więc zdefiniowane przez Einsteina wielkości pędu i energii relatywistycznej spełniają zasady zachowania, a dla małych prędkości względnych układów odniesienia przechodzą w definicje klasyczne - ale ostateczną weryfikacją sensu i poprawności tych definicji jest eksperyment!

Równoważność masy i energii

• Według przewidywań Einsteina, spoczywająca masa
zawiera olbrzymią ilość energii:

Nawet zmniejszenie masy spoczynkowej cząstki (np. w wyniku rozpadu promieniotwórczego - tzw. defekt masy) o niewielką ilość
spowodowałoby wyzwolenie potężnej energii.

Przykład:

Energia
węgla:

1. spalonego klasycznie w elektrociepłowni:

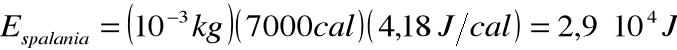
2. uzyskana z wyzwolenia z masy spoczynkowej:

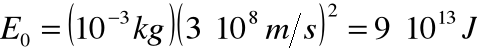
Relatywistyczna energia kinetyczna

• Definicja energii kinetycznej: część energii całkowitej cząstki, wynikająca z ruchu cząstki (a więc związana z jego prędkością) - definicja prawdziwa zarówno w mechanice klasycznej, jak i relatywistycznej.

• W mechanice relatywistycznej możemy więc obliczyć energię kinetyczną jako różnicę między energią całkowitą a energią spoczynkową:

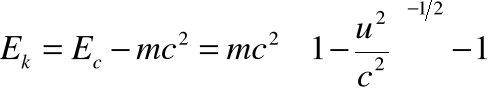
• Dla małych prędkości wykorzystujemy rozwinięcie dwumianu:

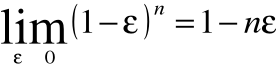
co daje nam ostatecznie znane wyrażenie:

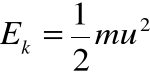
Relatywistyczny związek

między energią a pędem

• Korzystając z wprowadzonych definicji relatywistycznego pędu i energii (dla przypomnienia):

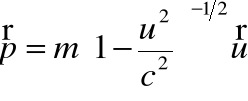
i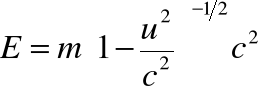

możemy znaleźć związki między pędem i energią w ujęciu relatywistycznym:

1. dzieląc stronami:

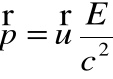
2. rugując z obu równań prędkość cząstki
   :

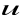
• Taka postać równań na pęd i energię implikuje jeszcze jeden ważny fakt - podstawowy dla mechaniki relatywistycznej: żadna cząstka materialna (
) nie może osiągnąć prędkości światła
, gdyż wtedy jej pęd i energia wzrosłyby do nieskończoności.

Masa relatywistyczna

• Można sformułować definicję pędu relatywistycznego cząstki na sposób „klasyczny” jako:

jeśli wprowadzimy pojęcie masy relatywistycznej:

gdzie
jest masą spoczynkową cząstki.

• Masa relatywistyczna to inaczej energia relatywistyczna podzielona przez stałą
- masa relatywistyczna układu odosobnionego jest zachowana, podczas gdy masa spoczynkowa, zawarta w indywidualnych cząstkach, może się zmieniać (zasada zachowania energii).

Zasada zachowania energii:

zderzenie niesprężyste

• Rozpatrzmy zderzenie niesprężyste: dwie identyczne cząstki zderzają się i łączą w inną, „wypadkową” cząstkę.

W układzie odniesienia
, związanym ze spoczywającym środkiem masy:

♥

podczas gdy w innym układzie odniesienia
będzie:

♠

Stosując transformacje Lorentza, możemy powyższe przetransformować do wielkości obserwowanych w układzie
:

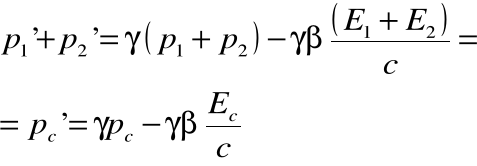
co po wykorzystaniu związków ♥ i ♠ doprowadzi nas do:

Energia relatywistyczna jest zachowana podczas tego zderzenia!

Cząstki o zerowej masie spoczynkowej

• Istnieją również cząstki, które nie mają masy spoczynkowej! Należą do nich np. fotony - kwanty promieniowania elektromagnetycznego. Teoria korpuskularna światła każe je traktować jak cząstki ze względu na to, że mają one pęd i energię, choć nie mają masy - właśnie masy spoczynkowej!

• Korzystając ze związku:

i podstawiając
otrzymujemy:

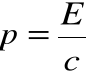
czyli związek między pędem i energią takiej „bezmasowej” cząstki, analogiczny do postulowanego przez de Broglie'a!.

• Korzystając z kolei ze związku:

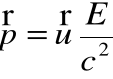
stwierdzimy, że prędkość cząstki o masie spoczynkowej równej 0 musi wynosić
!

Siła relatywistyczna

• Wygodnie jest również w mechanice relatywistycznej zdefiniować siłę tak, żeby III zasada dynamiki Newtona była słuszna dla dwóch oddziaływujących cząstek. Z kolei ze względu na zasadę zachowania pędu, „pozostawimy” definicję siły jako:

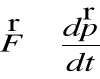
Przy takiej definicji jednak wartość i kierunek siły będą zależeć od prędkości poruszającego się obserwatora!

• Efekty, potwierdzające takie podejście, zostały zaobserwowane - w elektrodynamice pokazano, że np. stacjonarne pole elektryczne
jest „widziane” przez poruszającego się obserwatora jako pole magnetyczne o indukcji
równej:

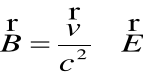
( w układzie CGS)

Fizycznie pola
i
dla poruszających się obserwatorów przechodzą wzajemnie jedno w drugie, a więc powinno się o nich myśleć jako o jednym polu elektromagnetycznym - w elektrodynamice współczesnej zwykło się nawet traktować pole magnetyczne jako „relatywistyczną manifestację” pola elektrycznego!

Ogólna teoria względności

• Podany dotąd „przepis” na mechanikę relatywistyczną nazywamy szczególną teorią względności. Została ona całkowicie opracowana przez Einsteina w 1905 r.

• Ogólna teoria względności była opracowana później, poczynając od 1911 r., przez Einsteina. Jest ona nowoczesną, relatywistyczną teorią grawitacji.

• Podstawą tej teorii jest zasada równoważności (masa grawitacyjna jest równoważna masie bezwładnej w tym sensie, że nie sposób doświadczalnie odróżnić jednej od drugiej).

• Jednym z wniosków tej teorii jest stwierdzenie, że obecność masy „odkształca” otaczającą ją przestrzeń i wobec tego poruszające się w takiej przestrzeni ciała mają tory zakrzywiające się ku masie, która to odkształcenie spowodowała, co powoduje powstanie przyspieszeń („normalne” w ruchu krzywoliniowym) i jest obserwowane jako działanie sił grawitacyjnych!

• Inną konsekwencją tej teorii są np.:

• powiększenie się długości fali światła emitowanego przez źródło, mające masę - grawitacyjne przesunięcie ku czerwieni;

• zakrzywianie się wiązki światła w pobliżu dużej masy.

15

---