Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 1

1. Dane są dwa wektory
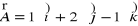
   i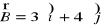
   . Obliczyć:

1. długość każdego wektora;

2. iloczyn skalarny tych wektorów;

3. kąt zawarty między wektorami;

4. iloczyn wektorowy tych wektorów.

1.2 Znaleźć wektor jednostkowy n prostopadły do dwóch wektorów
i
.

1.3 Wykazać, że wektor
jest prostopadły do wektora
, jeśli
.

1.4 Siła
działa na punkt
. Obliczyć:

1. moment siły względem początku układu współrzędnych;

2. moment siły względem punktu
   .

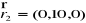
1.5 Dwie cząstki poruszają się wzdłuż osi OX i OY odpowiednio z prędkościami
i
[m/s]. W chwili t =0 są one w punktach o współrzędnych x₁=-3, y₁=0, x₂=0, y₂=-3 [m]. Znaleźć wektor
, który określi położenie drugiej cząstki względem pierwszej w funkcji czasu. Kiedy i gdzie obie cząstki będą najbliżej siebie?

1. Cząstka porusza się po linii prostej, przy czym zależność jej położenia od czasu określa równanie: x=6t+0.125t³ [m]. Znaleźć prędkość po drugiej i szóstej sekundzie oraz średnią wartość prędkości tej cząstki pomiędzy drugą a szóstą sekundą trwania ruchu.

1.7 Wyznacz gradient funkcji
dla:

a)
;

b)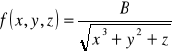
.

1.8 Wyznacz dywergencję wektora
, którego współrzędne są następującymi funkcjami:

a)
;

b)
.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 2

2.1 Od rakiety, która unosi się pionowo do góry, w momencie, gdy ma ona prędkość
oderwał się na wysokości
jeden z niepotrzebnych już zbiorników paliwa. Znaleźć czas, po którym zbiornik ten opadnie na Ziemię, oraz jego prędkość w chwili upadku.

2.2 Punkt materialny porusza się w płaszczyźnie XY, a jego ruch opisują równania:
,
, gdzie
są wielkościami stałymi. Znaleźć, po upływie czasu
prędkość i przyśpieszenie punktu oraz kąt pomiędzy wektorami prędkości i przyśpieszenia.

2.3 Przy powierzchni Ziemi rzucono poziomo ciało z prędkością
. Znaleźć przyśpieszenie styczne i normalne po czasie
_.

2.4 Bombowiec nurkuje po prostej pod kątem
do poziomu z prędkością
. Jeżeli pilot chce zrzucić bombę na wysokości
i trafić dokładnie w cel, to w jakiej odległości od celu powinien on to zrobić? Nie uwzględniać oporu powietrza.

2.5 Rybak płynie łódką w górę rzeki. Przejeżdżając pod mostem gubi zapasowe wiosło, które wpada do wody. Po godzinie rybak zauważył brak wiosła i zawrócił po nie, doganiając je
poniżej mostu. Jaka jest prędkość rzeki, jeśli rybak poruszając się w dół i w górę rzeki wiosłuje jednakowo?

1. Między dwoma punktami położonymi na rzece w odległości
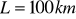
   kursuje kuter. Kuter przebywa tę odległość z prądem rzeki w czasie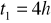
   , a przeciw prądowi w ciągu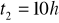
   . Wyznaczyć prędkość nurtu rzeki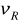
   i prędkość kutra względem wody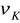
   .

2. Od jadącego wagonu pociągu odczepił się ostatni wagon. Pociąg nadal jedzie z tą samą prędkością. Jaka jest względna droga przebyta przez pociąg i wagon do chwili zatrzymania się wagonu? Zakładamy, że wagon porusza się ruchem jednostajnie opóźnionym.

3. Ciało spada swobodnie z wysokości
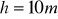
   . W tej samej chwili drugie ciało rzucono z wysokości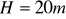
   pionowo w dół z pewna prędkością początkową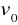
   . Wyznaczyć tę prędkość, jeśli oba ciała spadły na ziemię jednocześnie.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 3

3.1 Na stole przymocowano jedna za drugą masy
,
i
do masy
(rysunek lewy poniżej Znaleźć:

1. 
   
   
   przyśpieszenie układu,

2. naprężenia wszystkich nici.

Tarcie zaniedbać.

3.2 Do końca nici przerzuconej przez nieruchomy krążek przymocowano ciężar
. Na drugim końcu nici znajduje się krążek ruchomy, do którego zaczepiony jest ciężar
(rysunek prawy, powyżej). Wyznaczyć przyspieszenie każdego ciała i naprężenie nici. Nie uwzględniać tarcia i masy krążków.

3.3 Balon, którego całkowity ciężar wynosi
, opada w dół z prędkością
. Przyjmując, że wielkość siły wyporu wynosi
wyznacz masę balastu
, jaką należy wyrzucić z balonu, aby zaczął się on wznosić z taką samą prędkością? Załóż, że siła oporu ośrodka jest identyczna w czasie spadania i wznoszenia balonu.

3.4 Ciało o ciężarze
za pomocą nici przerzuconej przez nieważki krążek, ciągnie po równi pochyłej ciało o takim samym ciężarze (rys. poniżej). Wyznaczyć przyspieszenie, z jakim poruszają się oba ciężary, jeśli równia pochyła tworzy z poziomem kąt
, a współczynnik tarcia wynosi
.

3.5 Ciało swobodnie zsuwa się z wierzchołka równi pochyłej, której kąt nachylenia do poziomu wynosi
. Wyznaczyć prędkość ciała na końcu równi i czas ruchu, jeżeli wysokość równi wynosi
a współczynnik tarcia
.

3.6 Przy jednostajnym wciąganiu ciała o ciężarze
po równi pochyłej, tworzącej kąt
z pionem należy przyłożyć siłę
. Z jakim przyspieszeniem będzie zsuwało się swobodnie puszczone ciało w dół równi pochyłej?

3.7 Dwa ciała o masach
i
są związane nitka i leżą na gładkiej powierzchni poziomej. Z jaką siłą można ciągnąć pierwsze ciało, bez przerwania nici, jeżeli wytrzymuje ona naprężenie
? Czy wynik się zmieni, jeśli siłę przyłożymy do drugiego ciała?

3.8 Do ciężaru
o masie
zawieszono na sznurze ciężar
o masie
. Masa sznura wynosi
. Do ciężaru
przyłożono siłę
i skierowaną do góry. Wyznaczyć naprężenie sznura w górnym jego końcu i w środku.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 4

4.1 Łódka o ciężarze
unosi się nieruchomo na stojącej wodzie. Znajdujący się w niej człowiek o ciężarze
przechodzi z dziobu na rufę, na skutek czego łódka przesuwa się o
. Wyznaczyć długość łódki. Nie uwzględniać oporu wody.

4.2 Człowiek wskoczył do poruszającego się wózka. Jaka jest prędkość wózka z człowiekiem, jeśli masa człowieka wynosi
, masa wózka
, a początkowa prędkość wózka wynosiła
?

4.3 Gimnastyk o masie
trzyma w rękach kulę o masie
i skacze pod kątem
do poziomu z prędkością
. W chwili osiągnięcia maksymalnej wysokości gimnastyk rzuca kulę poziomo w kierunku odwrotnym do swego ruchu, nadając jej prędkość
względem Ziemi. Wyznaczyć długość skoku.

4.4 Rakieta leci z prędkością
. Po oddzieleniu się głowicy prędkość rakiety zmniejsza się dwukrotnie, a kierunek ruchu rakiety i głowicy pozostaje ten sam. Ile razy zwiększy się prędkość głowicy, jeżeli masa jej jest sześciokrotnie mniejsza od masy rakiety?

4.5 Dwie łódki poruszają się w stojącej wodzie ruchem jednostajnym z jednakowymi prędkościami
w przeciwnych kierunkach. Gdy łódki znajdują się naprzeciw siebie, z pierwszej do drugiej przerzucamy ładunek o masie
. Druga łódka nadal kontynuuje swój ruch w tym samym kierunku, lecz z prędkością
. Wyznaczyć masę drugiej łódki. Nie uwzględniać oporu wody.

4.6 Trzy łódki o jednakowym ciężarze
poruszają się jedna za drugą, z jednakową prędkością
. Ze środkowej łódki jednocześnie rzucono do pierwszej i ostatniej jednakowe ładunki o ciężarze
z prędkością
względem łódek. Jakie są prędkości łódek po przerzuceniu ładunków?

4.7 Człowiek stoi na platformie, która może swobodnie poruszać się po prostoliniowych szynach. Na początku człowiek i platforma są nieruchome. Następnie człowiek zaczyna się poruszać ruchem jednostajnym po platformie z prędkością
względem platformy. Wyznaczyć prędkość człowieka względem Ziemi, jeżeli waży on dziewięć razy mniej niż platforma.

4.8 Kulę o masie
zawieszoną na nici o długości
odchylamy od pionu o kąt
i puszczamy swobodnie. W chwili, gdy kula znajdzie się w położeniu równowagi rzucamy w nią poziomo, w kierunku przeciwnym do jej ruchu, kulkę o masie
. Zakładając, że uderzenie kulki jest centralne i że kula zatrzymuje się od razu po zderzeniu, wyznaczyć prędkość kulki w chwili zderzenia.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 5

5.1 Kwadrat o boku
, leżący w płaszczyźnie
ma w swych rogach ułożone masy
i
(rysunek). Obliczyć składowe tensora bezwładności względem osi X, Y, Z.

5.2 Do końca nici nawiniętej na bęben o promieniu
przywiązano masę
. Znaleźć moment bezwładności bębna, jeżeli wiadomo, że masa opuszcza się z przyśpieszeniem
.

5.3 Dwa odważniki o masach odpowiednio
i
są połączone nicią przerzuconą przez krążek. Promień krążka
, a jego masa
. Obliczyć:

1. przyspieszenie, z jakim poruszają się odważniki;

2. naciągi nici, na których są zawieszone odważniki.

5.4 Dwa ciała o masach
i
połączone są nieważką, nierozciągliwą nicią, przechodząca przez bloczek o masie
i promieniu
. Ciało o masie
spoczywa na równi pochyłej, która tworzy z poziomem kąt
(rysunek). Współczynnik tarcia ciała
o równię wynosi
. Wyznaczyć przyspieszenie układu. (Założyć, że układ porusza się w prawą stronę; czy rozwiązanie będzie istotnie inne, jeśli założymy ruch układu mas w lewo?).

5.5 Z równi pochyłej o kącie nachylenia
staczają się bez poślizgu kula i obręcz Prędkość początkowa obu brył wynosi zero. Która z nich szybciej osiągnie dół równi? Obliczyć przyspieszenia liniowe obu brył.

5.6 Ciężka szpula z nawiniętą nicią, do której przyłożono siłę
, leży na płaszczyźnie poziomej. W którą stronę i z jakim przyśpieszeniem będzie poruszała się szpula w zależności od kąta między kierunkiem działania siły a płaszczyzną poziomą. Masa szpuli
, promień zewnętrzny i wewnętrzny szpuli odpowiednio
i
; moment bezwładności względem osi przechodzącej przez środek równy jest
.

5.7 Listwa drewniana o długości
i masie
może obracać się dookoła osi prostopadłej do listwy, przechodzącej przez jej środek. W koniec listwy trafia pocisk o masie
, lecący z prędkością v w kierunku prostopadłym do osi listwy. Znaleźć prędkość kątową
, z jaką listwa zaczyna się obracać, gdy utkwi w niej pocisk.

5.8 Dwie poziome tarcze o momentach bezwładności odpowiednio
oraz
wirują niezależnie wokół pionowej osi przechodzącej przez ich środek. Prędkości kątowe obu tarcz wynoszą odpowiednio
i
. W pewnym momencie górna tarcza („1”) opada na dolną i w wyniku działania sił tarcia obie obracają się dalej jak jedno ciało. Wyznaczyć prędkość kątową obu tarcz po ich złączeniu oraz pracę wykonaną przez siły tarcia.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 6

6.1 Mała kulka zawieszona na nici o długości
zatacza okrąg o promieniu
. Jaki jest czas obiegu kulki po okręgu?

6.2 Kulkę o masie
zawieszono na nici do ciała
o masie
. Następnie kulkę popchnięto tak, że zaczęła krążyć po okręgu o promieniu
w płaszczyźnie poziomej. Jaki jest współczynnik tarcia
, jeśli czas obiegu kulki wynosi
?

6.3 Mała kulka stacza się po zjeżdżalni zakończonej pętlą o promieniu
. Jaka powinna być wysokość
zjeżdżalni, aby kulka:

a) nie odpadła od pętli,

b) odpadła na wysokości
?

6.4 Jaki promień okręgu może zakreślić rowerzysta jadący z prędkością
, jeśli graniczny kąt wychylenia rowerzysty od pionu wynosi
?

6.5 Regulator Watta wykonuje
. O jaki kąt odchylą się przy tym drążki zakończone kulami o masie
? Długość każdego drążka wynosi
. Pominąć masę wszystkich części z wyjątkiem kul.

6.6 Jaki jest najmniejszy promień okręgu, po którym może jechać łyżwiarz poruszający się z prędkością
, jeżeli współczynnik tarcia przy ślizganiu się łyżew o powierzchnię lodu wynosi
? Jaki jest największy kąt nachylenia łyżwiarza w stosunku do pionu, przy którym nie nastąpi upadek na zakręcie?

6.7 Wewnątrz wydrążonej kuli o promieniu
znajduje się mała kulka o promieniu
. Dużą kulę wprawiono w ruch obrotowy dookoła osi pionowej z prędkością kątową
. Wyznaczyć położenie równowagi małej kulki.

6.8 Pocisk wystrzelono z prędkością
skierowaną pod kątem
do poziomu z działa znajdującego się na półkuli północnej w miejscowości o szerokości geograficznej φ skierowanego na południe. Oblicz odchylenie pocisku od osi celowniczej w chwili upadku na Ziemię.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 7

7.1. Samochód jedzie pod górę po niewielkim wzniesieniu ze stałą prędkością
. Przy jeździe w kierunku odwrotnym (z góry) osiąga on przy takiej samej mocy silnika prędkość
. Jaką prędkość osiągnie samochód przy tej samej mocy silnika jadąc po drodze poziomej? Zakładamy, że siła poruszająca nie zależy od prędkości. Uwzględnić tarcie.

7.2 Winda o ciężarze
wyciągana jest do góry ze stałym przyspieszeniem
. Jaką pracę należy wykonać, aby podnieść windę na wysokość
?

7.3 Kierowca samochodu jadącego z prędkością
nagle zobaczył przed sobą w odległości
szeroką ścianę. Co ma zrobić kierowca, by uniknąć zderzenia: zacząć hamować czy skręcać w bok?

7.4 Na powierzchni ziemi leży poziomo
jednorodnych płyt, jednak obok drugiej. Każda płyta ma ciężar
i grubość
. Jaką najmniejszą (teoretycznie) pracę należy wykonać, aby ułożyć płyty jedna na drugą, w kształcie kolumny?

7.5 Łyżwiarz stojąc na łyżwach rzuca do przodu w kierunku poziomym kamień o ciężarze
z prędkością
. Wyznaczyć współczynnik tarcia łyżew o lód i pracę wykonaną przez łyżwiarza, jeśli jego ciężar jest równy
i jeśli po rzucie cofnął się on na odległość
.

7.6 Karabin o masie
zawieszony jest poziomo na dwóch równoległych niciach. Podczas wystrzału, na skutek odrzutu karabin wychylił się do góry o
. Masa kuli wynosi
. Wyznaczyć prędkość wylotu kuli.

7.7 Z działa o masie
wylatuje w kierunku poziomym pocisk o masie
. Jaka cześć pracy wykonanej przez gaz prochowy jest zamieniona na prace odrzutu działa?

7.8 Pompa napełnia basen wodą w ciągu
. Znaleźć moc silnika pompy, jeżeli pojemność basenu wynosi
, a jego środek znajduje się na wysokości
nad powierzchnią wody jeziora, z którego czerpana jest woda. Współczynnik sprawności pompy
.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 8

8.1 Maksymalna wysokość pierwszego sputnika Ziemi wynosiła
. Jaką prędkość liniową musiał mieć wtedy sputnik, jeśli dalszy jego ruch odbywał się po orbicie kołowej? Promień Ziemi
.

8.2 Na linii prostej łączącej Ziemię i Księżyc znaleźć punkt o tej własności, że znajdujące się w nim ciało jest przyciągane przez Księżyc i Ziemię z tą samą siłą. Odległość między Ziemią i Księżycem przyjąć za równą 60 ziemskim promieniom, a masa Księżyca jest 81 razy mniejsza od masy Ziemi.

8.3 Wyznaczyć liczbę obrotów satelity dookoła Ziemi w ciągu doby, jeśli porusza się on po orbicie kołowej o promieniu
.

8.4 Jaką prędkość poziomą względem powierzchni Ziemie należy nadać rakiecie lecącej w niewielkiej odległości od tej powierzchni wzdłuż równika, aby po wyłączeniu silników rakieta nie spadając na Ziemię zaczęła poruszać się po orbicie kołowej dookoła Ziemi (tzn. stała się jej sztucznym satelitą)? Nie uwzględniać oporu atmosfery.

8.5 Wyznaczyć odległość od środka Ziemi do sztucznego satelity oraz wyznaczyć jego prędkość liniową, jeżeli satelita ten porusza się w płaszczyźnie równika w kierunku obrotu Ziemi z taką prędkością, że jest on nieruchomy względem Ziemi. Promień Ziemi
.

8.6 Średnica planetoidy równa jest
. Zakładając, że gęstość materii planetoidy wynosi
, znaleźć przyspieszenie grawitacyjne
na jej powierzchni i obliczyć, na jaką wysokość podskoczył człowiek znajdujący się na jej powierzchni, jeżeli w wykonanie skoku włożył tyle samo wysiłku ile potrzeba, aby podskoczyć na wysokość
na powierzchni Ziemi.

8.7 Wyznaczyć przyspieszenie ziemskie na wysokości
nad powierzchnią Ziemi, przyjmując przyspieszenie na powierzchni równe
. Promień Ziemi
.

8.8 Wyznaczyć stosunek ciężarów ciała na równiku i biegunie planety, której promień jest równy
, masa
a doba wynosi
.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 9

9.1 Układ K^' porusza się względem osi OX układu odniesienia K ze stałą prędkością
. W układzie K^' znajduje się pręt o długości własnej
, tworzący z osią OX^' kąt
. Jaką długość pręta
i jaki kąt
zmierzy obserwator w układzie K (nieruchomym)?

9.2 Ile razy wzrasta gęstość ciała poruszającego się z prędkością
w stosunku do gęstości ciała spoczywającego?

9.3 Dwa akceleratory dają cząstki poruszające się w przeciwne strony z prędkościami
i
. Obliczyć względną prędkość cząstek.

9.4 Wyznaczyć masę oraz prędkość elektronu, którego energia kinetyczna wynosi
.

9.5 Mezon μ utworzony w górnych warstwach atmosfery przebywa do chwili rozpadu odległość
poruszając się z prędkością
. Jaki jest czas życia mezonu mierzony przez nas, a jaki mierzony w jego własnym układzie odniesienia? Jaka jest grubość atmosfery przebyta przez mezon, zmierzona w jego własnym układzie odniesienia?

9.6 Jakie powinno być napięcie pola elektrycznego, aby zgodnie z zasadami mechaniki klasycznej poruszający się w tym polu elektron uzyskał prędkość światła? Jaką prędkość w tym polu uzyska według mechaniki relatywistycznej?

9.7 Słońce emituje w ciągu sekundy energię równą
. Przyjmując, że moc promieniowania Słońca jest stała, znaleźć czas, w ciągu którego masa Słońca zmaleje do połowy. Masa Słońca
.

9.8 W spoczywającą cząstkę o masie
uderza cząstka o masie spoczynkowej
i energii kinetycznej
. W wyniku zderzenia obie cząstki zespalają się w jedną i poruszają się dalej w całości. Znaleźć masę spoczynkową powstałej cząstki oraz jej prędkość.

Zadania z fizyki dla I roku Wydziału Mech. Energetycznego - LISTA 10

10.1 Równanie ruchu punktu dane jest w postaci:
. Znaleźć te chwile, w których występuje maksymalna prędkość i maksymalne przyśpieszenie.

10.2 Energia całkowita ciała drgającego harmonicznie jest równa
a maksymalna siła działająca na ciało
. Napisać równanie ruchu tego ciała, jeśli okres drgań trwa
a faza początkowa wynosi
.

10.3 Na gumce o długości
i promieniu
wisi odważnik o masie
. Wiedząc, że moduł Younga tej gumy wynosi
, znaleźć okres
pionowych drgań odważnika.

10.4 Areometr o masie
pływa w cieczy. Gdy zanurzy się go w cieczy i puści, zaczyna wykonywać drgania z okresem
. Przyjmując, że drgania są nietłumione, znaleźć gęstość cieczy, w której pływa areometr. Średnica walcowej rurki areometru wynosi

10.5 Przez Ziemię przewiercono tunel. Do tunelu wpuszczono kulkę. Znaleźć czas potrzebny do osiągnięcia przez kulkę środka Ziemi, a także prędkość, z jaką kulka minie środek Ziemi.

10.6 Jak zmieni się okres drgań pionowych masy wiszącej na dwóch jednakowych sprężynach, gdy połączenie szeregowe sprężyn zostanie zastąpione połączeniem równoległym?

10.7 Drgania zadane są równaniem
, gdzie amplituda zmienia się w czasie zgodnie z zależnością
. Znaleźć składowe harmoniczne tych drgań.

10.8 Okres drgań tłumionych jest równy
, dekrement tłumienia
, a faza początkowa wynosi zero. Wychylenie punktu w chwili
jest równe
. Napisz równanie ruchu tych drgań.

14

M

m₁

m₂

m₃

M

M

m

X

Y

m

A

P

Q

m₂

m₁

M

---