xxxxxxxxxxx xxxxxxxx xxxxxxxxxxx xx xxxxxxxxxx xxxxxxxxxx

xx xx xx xx xx xx xx xx xx

xx xx xx xx xx xx xx xx xx

xx xxxxxxxx xx xx xx xxxxxxxx

xx xx xx xx xx xx xx xx

xx xx xx xx xx xx xx xx

xx xx xx xx xxxxxxxxxx xxxxxxxxxx

---------------------------------------------------------------------------------------------------------by aikon—

Strumienie ruchu

A - ruch generowany, jego źródłem są terminale (np. abonenci), rozdziela się na ruch wewnętrzny (F) i ruch generowany wychodzący (G)

B - ruch przychodzący, jego źródłem są inne centrale. Rozdziela się na tranzytowy (T) i przychodzący końcowy (K)

Q - ruch końcowy, sumaryczny strumień którego ujściem są terminale. Składa się z ruchu wewnętrznego (F) i ruchu przychodzącego końcowego (K)

R - ruch wychodzący, jego ujściem są terminale innych central sieci, składa się z ruchu generowanego wychodzącego (G) i ruchu tranzytowego (L).

F - część ruchu generowanego, którego ujściem są terminale tej samej centrali

G - część ruchu generowanego, którego ujściem są terminale innej centrali

K - część ruchu przychodzącego, którego ujściem są terminale rozpatrywanej centrali

T - część ruchu przychodzącego, którego ujściem są terminale innych central sieci

Intensywność wywołań, natężenie ruchu

Intensywność wywołań - całkowita liczba zgłoszeń kierowanych do abonenta na jednostkę czasu.

Jednostką jest 1/t (t - jednostka czasu, zazwyczaj minuta). Oznaczenie: λ

Natężenie ruchu:

- chwilowe - ilość połączeń istniejących jednocześnie na danym odcinku

- średnie - średnia arytmetyczna z wartości wszystkich chwilowych natężeń ruchu na danym odcinku w kolejnych chwilach obserwacji.

Średnie natężenie ruchu:

1) A = λ ∙ h

λ - średnia liczba zgłoszeń na jednostkę czasu

h - średni czas trwania połączenia

2)
T - okres obserwacji

t_k - czas trwania k-tego połączenia

c - ilość zestawionych połączeń

Jest jeszcze kilka innych wzorków ale wszystkie w wyniku dają zawsze i tak to samo, więc analizę pozostawiamy czytelnikowi

Jednostką średniego natężenia ruchu jest Erlang (Erl), czyli jedna połączenio-godzina na godzinę (najprościej mówiąc - stosunek czasu zajętości do czasu obserwacji).

1 Erl = 60 PM (połączenio-minuty)

1 Erl = 36 CCS (Hundred Call Seconds)

Sprawność systemu

Wszystkie zgłoszenia napływające do systemu stanowią ruch oferowany. Nie wszystkie połączenia kończą się rozmową. Zgłoszenia nie obsłużone stanowią ruch stracony. Ruch zakończony zestawieniem połączenia stanowią ruch załatwiony. Z punktu widzenia systemu usługa została zrealizowana niezależnie od tego, czy połączenie zakończy się rozmową, czy nie (np. zajęte albo abonent nie odbiera).

Sprawność użytkowa systemu:

c_r - liczba zgłoszeń, które zakończyły się rozmową

c - całkowita liczba zgłoszeń

Godzina największego ruchu

Jest to okres 60 kolejnych minut w ciągu doby, podczas którego średnie natężenie ruchu jest największe. Aby wyznaczyć średnie natężenie ruchu w GNR, potrzebny jest współczynnik skupienia.

c_d - liczba połączeń wychodzących z danej grupy źródeł w ciągu doby

c - liczba połączeń wychodzących z danej grupy w ciągu godziny największego ruchu

T - czas obserwacji

Systemy załatwiania ruchu

Podział systemów ze względu na załatwianie ruchu

• System ze stratami zgłoszeń - zgłoszenie napotykające na blokadę jest tracone i nie jest dalej obsługiwane. Przyjmuje się, że czasy trwania tych połączeń są równe 0. Nie ma kolejki (czyli c_p = 0, gdzie c_p - długość kolejki)

• Systemy z opóźnianiem zgłoszeń - po napotkaniu blokady urządzenie oczekuje w poczekalni na zwolnienie niezbędnych zasobów. Natychmiast po zwolnieniu zasobów rozpoczyna się obsługa oczekującego zgłoszenia. Przyjmuje się, że liczba miejsc w kolejce jest wystarczająco duża (c_p = ∞ ).

• Systemy mieszane - mające cechy obydwu powyższych, ale przyjmuje się, że ilość miejsc w poczekalni jest ograniczona (0 < c_p < ∞).

Miara jakości obsługi:

- współczynnik blokady (natłoku)

Tb - czas blokady

T - czas obserwacji

- współczynnik strat

c_s(T) - liczba zgłoszeń straconych

c_z(T) - liczba zgłoszeń załatwionych

c(T) - całkowita liczba zgłoszeń w czasie T

Klasyfikacja systemów - notacja

Notacja A.M. Lee:

A/B/N/c_p/S

A - rodzaj wejściowego strumienia zgłoszeń

B - typ rozkładu czasów obsługi

N - liczba stanowisk obsługi

c_p - pojemność poczekalni

S - liczba źródeł ruchu

Możliwe opcje:

A M - strumień poissonowski, D - zgłoszenie regularne deterministyczne, G - brak założeń

B M - rozkład wykładniczy czasu obsługi, D - stały czas obsługi, G - dowolny rozkład

N tu jakaś liczba całkowita

c_p jakaś liczba całkowita (0 - bez poczekalni, brak wartości - nieskończenie duża kolejka)

S jakaś liczba całkowita (jak nie ma podanej oznacza nieskończoną ilość źródeł ruchu)

Strumienie zgłoszeń

• Jednorodne - charakteryzuje je zawsze jedna cecha i mogą być opisane jednoznacznie za pomocą:

• Ciągu chwil napływu zgłoszenia

• Ciągu przedziałów czasu między zgłoszeniami

• Ciągu liczb pojawiających się zgłoszeń w zadanych przedziałach czasu

• Niejednorodne - charakteryzują je przynajmniej dwie cechy

• Zawsze jedną z cech jest chwila napływu zgłoszenia

• Pozostałe cechy wyróżniają dane zgłoszenie spośród innych różnych od niego zgłoszeń

Strumień prosty - cechy:

• Stacjonarność - prawdopodobieństwo pojawienia się pewnej liczby zgłoszeń w jakimś przedziale czasu zależy tylko od długości tego przedziału, a nie zależy od jego położenia na osi czasu

• Brak pamięci - dla dowolnych rozłącznych przedziałów czasu liczba zgłoszeń, które wystąpią w jednym z nich, nie zależy od liczby zgłoszeń zachodzących w pozostałych przedziałach

• Pojedynczość - niemożność pojawienia się dwóch lub większej liczby zgłoszeń w tym samym czasie.

Strumień generowany przez nieskończoną liczbę źródeł ruchu strumień Poissona

Odstępy między zgłoszeniami w strumieniu Poissona są zmiennymi losowymi o charakterze wykładniczym.

Cechy strumienia Poissona:

- prawdopodobieństwo napływu „k” zgłoszeń w przedziale czasu „t”

- prawdopodobieństwo, że w czasie „t” nie pojawi się żadne zgłoszenie (czyli że czas do następnego zgłoszenia jest większy od „t” )

- prawdopodobieństwo, że w czasie „t” pojawi się zgłoszenie (czyli że czas do następnego zgłoszenia jest mniejszy lub równy „t”) - dystrybuanta

Modele ruchu telekomunikacyjnego

1) Modele ze stratami zgłoszeń

a) Model Erlanga (M/G/N/0 lub M/M/N/0)

Główne założenie: S >> N

przy czym: S ∞ , N przyjmuje wartości skończone

(S - liczba źródeł ruchu, N - liczba aparatów obsługi)

Pozostałe założenia:

- Intensywność zgłoszeń grupy źródeł ruchu jest stała i nie zależy od liczby zgłoszeń obsługiwanych w danej chwili.

- strumień zgłoszeń jest strumieniem Poissona

- istnieje stan równowagi statystycznej

- zgłoszenia napotykające na blokadę są tracone, a czas ich połączenia jest równy zeru

Wzorki:

Prawdopodobieństwo blokady (tzw. wzór B-Erlanga lub pierwszy wzór Erlanga)

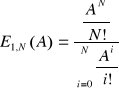
Zależność rekurencyjna:

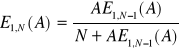
, przy liczeniu wykorzystujemy fakt, że: E_1,0(A) = 1

Współczynnik strat:

Ruch załatwiony

b) Model Engseta (M/G/N/0/S lub M/N/N/0/S)

Główne założenie: S > N

przy czym S i N przyjmują wartości skończone.

Intensywność zgłoszeń maleje wraz ze wzrostem liczby aktualnie obsługiwanych zgłoszeń.

Liczba nowych wywołań jest proporcjonalna do liczby łączy wolnych w danej chwili.

Wzorki:

- prawdopodobieństwo blokady (tzw. wzór Engseta)

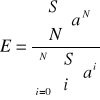
, gdzie a=λ/μ , śr. nat. ruchu oferowanego przez jedno wolne źródło

- prawdopodobieństwo strat

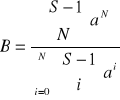
B < E !!

- średnie natężenie ruchu oferowanego

- średnie natężenie ruchu załatwianego

a - średnia wartość natężenia ruchu pojedynczego źródła ruchu

S - liczba źródeł ruchu

B - współczynnik strat ruchu

c) Model Bernoulliego

Główne założenie: S ≤ N

S, N - wartości skończone

Intensywność wywołań w stanie x :

Współczynnik strat w modelu Bernoulliego: B = 0 !!!

Współczynnik blokady (natłoku) :

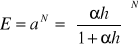
Skoro nie ma strat, to ruch oferowany i załatwiany są równe: A = A_z = S ∙ a

2) Modele z oczekiwaniem

a) Model Erlanga (M/M/N)

Założenia:

- N stanowisk obsługi

- czasy między zgłoszeniami są zmiennymi losowymi o rozkładzie wykładniczym

- czasy obsługi są zmiennymi losowymi o rozkładzie wykładniczym

- wywołania napotykające na blokadę trafiają do kolejki, gdzie czekają na zwolnienie się stanowisk obsługi.

Warunek równowagi statystycznej: A < N (inaczej kolejka rosłaby do nieskończoności).

Przy czym A = λ/μ (μ jest intensywnością obsługi).

Prawdopodobieństwo blokady (tzw. drugi wzór Erlanga lub wzór C-Erlanga):

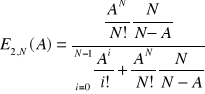
Związek między pierwszym i drugim wzorem Erlanga:

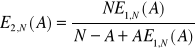
Średni czas oczekiwania w kolejce odniesiony do wszystkich wywołań (zarówno oczekujących

jak i nie oczekujących)

Średni czas oczekiwania odniesiony do wywołań opóźnionych :

Średnia liczba wywołań oczekujących w kolejce:

Ważne pojęcia

Równowaga statystyczna - w danym stanie prawdopodobieństwo nowego wywołania jest równe prawdopodobieństwu zakończenia obsługi jakiegoś innego wywołania. Intensywność strumienia wpływającego do jakiegoś stanu jest równa intensywności strumienia wypływającego z tego stanu.

Proces urodzin i śmierci - szczególny przypadek łańcucha Markowa. Dopuszcza tylko przejścia między stanami sąsiednimi. Czas może być ciągły lub dyskretny.

Prawo wiązki - przy łączeniu małych wiązek łączy w większe wiązki maleje współczynnik strat czyli rośnie średnia obciążalność łącza wiązki. Zakłada się wiązkę doskonałą ze stratami zgłoszeń i model Erlanga. Średnia obciążalność rośnie bardzo szybko dla małych wiązek, zaś bardzo powoli dla dużych wiązek. Łączenie wiązek jest kosztowne i skomplikowane technicznie, dlatego unika się wiązek zbyt dużych. W praktyce wiązki łączy się razem do wielkości 60-180 łączy.

Twierdzenie Closa - dwustronne trzysekcyjne pole komutacyjne Closa v(m,n,r) jest nieblokowalne w wąskim sensie wtedy i tylko wtedy, gdy m ≥ 2n-1.

ZADANIA

Zad. 1.

Zaobserwowano następujące cztery zajętości łącza (rysunek). Wyznaczyć średnią wartość natężenia ruchu telekomunikacyjnego.

Rozwiązanie:

1) A = λ ∙ h

λ = 4/10 (ilość połączeń do czasu obserwacji)

h = 6/4 (średni czas połączenia)

A = 6/10 [Erl]

2)

3)

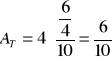
Zad. 2.

Na wiązkę składającą się z 3 łączy oferowany jest ruch o średnim natężeniu 1 Erl. Zakładany, że ruch ma charakter Poissonowski, a wybór dowolnego łącza w wiązce jest losowy o rozkładzie równomiernym (czyli jednakowe prawdopodobieństwo wyboru dowolnego łącza). Czas zajętości (czas trwania rozmowy) wynosi średnio 2 minuty.

1) Oblicz prawdopodobieństwo, że czas pomiędzy zgłoszeniami jest mniejszy lub równy 2 minuty

2) Oblicz prawdopodobieństwo, że czas pomiędzy zgłoszeniami jest większy niż 2 minuty

3) Oblicz prawdopodobieństwo, że na pierwszym łączu zgłoszenie pojawi się wcześniej niż po upływie 2 minut.

Rozwiązanie:

1)

A = λ ∙ h

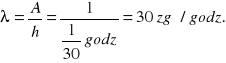
2)

3)

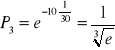
7

---