1. Pojęcie zmiennej losowej; zmienna losowa skokowa i ciągła. Rozkład normalny

Zmienna losowa w dosłownym tłumaczeniu oznacza:
- zmienna - przy wielokrotnym powtarzaniu jakiejś próby uzyskamy w większości przypadków różne wartości
- losowa - nie wiemy, jaka wartość będzie przed wykonaniem próby

Definicja (jedna z możliwych):
Zmienna losowa jest to taka zmienna, która w wyniku doświadczenia przybiera jedną i tylko jedną wartość ze zbioru tych wszystkich wartości, jakie ta zmienna może przyjąć.

Zmienną losową jest zmienna, która przyjmuje różne wartości wyznaczone przez los. Jest to funkcja, która zdarzeniom losowym przypisuje liczby.

Mówimy, że X jest zmienną losową skokową (dyskretną), jeśli jej zbiór wartości jest zbiorem skończonym lub przeliczalnym.

Przykłady zmiennych losowych dyskretnych:
- liczby urodzeń w Polsce
- ocena uzyskiwana przez studentów na egzaminie z wybranego przedmiotu.

Zmiennymi losowymi ciągłymi nazywamy takie zmienne losowe, które mogą przybierać dowolne wartości liczbowe z pewnego przedziału liczbowego.
Przykłady zmiennych losowych ciągłych:
- wzrost, waga, wiek człowieka

Rozkład normalny

Rozkład normalny, jest funkcją ciągłą, a więc może przyjmować dowolne wartości x
z przedziału (-∞, +∞). Każdej wartości x przypisuje odpowiednią wielkość f(x) zwaną gęstością prawdopodobieństwa. Prawdopodobieństwo zdarzenia, że zmienna X przyjmie wartość należąca do pewnego przedziału (x₁, x₂), zapisujemy:

X₂

P(x₁ ≤ X ≤ x₂) = x₁∫ f(x) dx

Kształt tej funkcji zależy od dwóch parametrów: średniej m i wariancji σ² (względnie odchylenia standardowego σ) N(m, σ). Jest to krzywa symetryczna względem swojej wartości średniej
o charakterystycznym kształcie „dzwonu”, którego spłaszczenie (wysmukłość) zależy od odchylenia standardowego. Większe odchylenie standardowe - „dzwon” bardziej smukły (przy tej samej średniej m). Większa średnia przy tym samym odchyleniu standardowym przesuwa funkcje w prawo. Punkt przegięcia krzywej znajduje się w odległości jednego odchylenia standardowego od średniej.

Rozkład normalny, zwany również rozkładem Gaussa jest jednym z najważniejszych rozkładów funkcji.

JEDNĄ Z NAJWAŻNIEJSZYCH WŁASNOŚCI ROZKŁADU NORMALNEGO JEST FAKT, ŻE PRZY PEWNYCH ZAŁOŻENIACH, ROZKŁAD SUMY DUŻEJ LICZBY ZMIENNYCH LOSOWYCH JEST
W PRZYBLIŻENIU NORMALNY (centralne twierdzenie graniczne)

2. Wartość średnia zmiennej losowej i wariancja zmiennej losowej

W rachunku prawdopodobieństwa wartość oczekiwana (inaczej wartość przeciętna, wartość średnia, nadzieja matematyczna)(dyskretnej) zmiennej losowej jest sumą iloczynów wartości tej zmiennej losowej oraz prawdopodobieństw, z jakimi te wartości są przyjmowane.

Formalnie, jeżeli dyskretna zmienna losowa X przyjmuje wartości x₁, x₂, ... odpowiednio z prawdopodobieństwami p₁, p₂, ..., wówczas wartość oczekiwaną E[X] zmiennej losowej X definiujemy jako:

Ogólnie, jeżeli X jest zmienną losową zdefiniowaną na przestrzeni probabilistycznej (Ω, F, P), to wartość oczekiwaną E[X] zmiennej losowej X definiujemy jako całkę :

Zatem jeśli X jest zmienną losową o funkcji gęstości prawdopodobieństwa f(x), to jej wartość oczekiwana wynosi

Wartość oczekiwana to inaczej pierwszy moment zwykły. Estymatorem wartości oczekiwanej rozkładu cechy w populacji jest średnia arytmetyczna.

Własności

Jeżeli istnieją E[X] i E[Y] to:

• 
  (liniowość);

• Jeżeli zmienne X,Y są niezależne, to E[XY] = E[X]E[Y]

Wariancja to klasyczna miara zmienności.

Wariancją w zbiorze wyników nazywamy przeciętne kwadratowe odchylenie poszczególnych wyników od średniej.

3. Kowariancja i współczynnik korelacji

Parametrami charakteryzującymi łączny rozkład dwuwymiarowej zmiennej losowej (X,Y) są kowariancja i współczynnik korelacji, za pomocą których mierzymy zależność pomiędzy zmiennymi losowymi.

Kowariancja Cov(X,Y) jest to liczba określająca zależność liczbową między zmiennymi losowymi X,Y. Jeżeli zmienne losowe X,Y są niezależne i istnieją ich wartości oczekiwane to Cov(X,Y)=0

Kowariancja-suma iloczynów odchyleń od średniej.

X i Y zmienne losowe takie, że ∃ E(X²), E(Y²) <∞

Cov (X,Y) : = E((X-E(X))(Y-E(Y)))

Kowariancja jest miarą nieunormowaną. Unormowana kowariancja nosi nazwę współczynnika korelacji. Współczynnik korelacji to kowariancja odniesiona do iloczynu odchyleń standardowych.

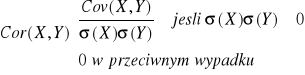
4. Pojęcie estymatora. Co to jest estymator nieobciążony, obciążony, asymptotycznie nieobciążony

Estymator jest narzędziem wnioskowania statystycznego. Estymator jest to funkcja wyników z próby, czyli statystyka służąca do oszacowania nieznanej wartości parametru populacji. Estymator jako funkcja wyników próby losowej, będących zmiennymi losowymi, jest zmienną losową.

Estymator jest nieobciążony, jeśli wartość oczekiwana rozkładu estymatora jest równa wartości szacowanego parametru.

Estymator jest obciążony, jeśli różnica pomiędzy wartością oczekiwaną rozkładu estymatora a wartością szacowanego parametru jest zależna funkcyjnie od estymatora.

Estymator nazywamy asymptotycznie nieobciążonym, jeśli obciążenie estymatora dąży do zera przy rosnącej liczebności próby.

5. Metoda momentu uzyskiwania estymatorów

Jeśli nie jest oczywiste jaką statystykę należy wybrać jako kandydata na estymator, z pomocą przychodzą różnorodne metody ich wyznaczania. Metoda momentów jest najstarszą metodą wyznaczania estymatorów. Polega ona na tym, że do szacowania parametrów populacji generalnej używamy odpowiednich momentów z próby lub ich funkcji.

Jeśli chcemy oszacować wartość średnią, to ponieważ jest to pierwszy moment, jako estymatora używamy pierwszego momentu z próby.

Chcąc oszacować wariancje, jako estymatora używamy drugiego momentu centralnego z próby. Metoda momentów odznacza się dużą prostotą, ale estymatory uzyskane przy pomocy tej metody nie mają na ogół dobrych własności.

6. Pojęcie przedziału ufności. Przedział ufności dla średniej normalnej, gdy sigma jest znana. Przedział ufności dla średniej normalnej, gdy sigma jest nieznana. Przedział ufności dla wariancji.

Przedziałem ufności nazywamy przedział (θ_1, θ₂), którego krańce są zmiennymi losowymi, a który zawiera nieznany parametr θ₂ z prawdopodobieństwem równym 1-ά

_ _____ _____

x_n - t ά √nS²n ; x_n + t ά √nS²n , jest to przedział ufności dla średniej

n(n-1) n(n-1)

normalnej m na poziomie ufności 1-ά, gdy wariancja ∂² jest nieznana.

Przedział ten ma zastosowanie w przypadku próby o małej liczebności, tj. n ≤ 30.

x_n - U ά ∂ ; x_n + U ά ∂ , jest to przedział ufności dla średniej normalnej, gdy

√n √n - te znaczki przed n to pierwiastki

wariancja ∂² jest znana. Przedział ten ma zastosowanie w przypadku próby o dużej liczebności, tj. n>30.

7. Pojęcie hipotezy statystycznej. Pojęcie statystyki testowej. Pojęcie zbioru krytycznego.

Błąd I-go rodzaju, błąd II-go rodzaju.

Obok zagadnień estymacji, drugim podstawowym działem wnioskowania statystycznego jest weryfikacja (podejmowanie decyzji o prawdziwości albo fałszywości) hipotez statystycznych

Def.: Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się w oparciu o pobraną próbkę. Przypuszczenia te dotyczą najczęściej postaci rozkładu lub wartości jego parametrów. Hipotezy, które dotyczą wyłącznie wartości parametru określonej klasy rozkładów nazywamy hipotezami parametrycznymi. Każdą hipotezę, która nie jest parametryczna, nazywamy hipotezą nieparametryczną. Jeżeli hipoteza parametryczna precyzuje dokładnie wartości wszystkich nieznanych parametrów rozkładu badanej cechy, to nazywamy ją prostą. W przeciwnym wypadku mamy do czynienia z hipotezą złożoną. Weryfikację hipotezy statystycznej przeprowadzamy w oparciu o wyniki próby losowej.

Metodę postępowania, która każdej możliwej realizacji próbki x_1, x _{2 ,} x _n przyporządkowuje z ustalonym prawdopodobieństwem decyzję przyjęcia lub odrzucenia sprawdzanej hipotezy nazywamy testem statystycznym. W praktyce przy weryfikacji hipotezy postępuje się tak, że oprócz weryfikacji hipotezy H₀ wyróżnia się inną hipotezę H₁, która najczęściej wynika z celu badania statystycznego, zwaną hipotezą alternatywną. Hipoteza H₁ jest taką hipotezą, którą w danym zagadnieniu skłonni jesteśmy przyjąć, jeśli weryfikowaną hipotezę H₀ należy odrzucić. W celu zbudowania testu do weryfikacji postawionej hipotezy H₀ należy wybrać odpowiednią funkcję próby losowej ∂ (x_1, x _{2 ,} x _n). Funkcję tę nazywamy statystyką testową. Przy pobieraniu próbek, nawet o tej samej liczności n, funkcja ta przyjmuje na ogół różne wartości, z których jedne będą świadczyły raczej o zgodności z weryfikowaną hipotezą, a inne mogą przemawiać przeciw tej hipotezie. Zachodzi więc konieczność podziału zbioru wszystkich wartości, które może przyjąć statystyka testowa na dwa dopełniające się zbiory w i w' takie, że jeśli ∂ (x_1, x _{2 ,} x _n) € w, hipotezę odrzucamy. Jeśli ∂ (x_1, x _{2 ,} x _n) € w', hipotezę przyjmujemy.

Zbiór W nazywamy zbiorem krytycznym lub zbiorem odrzuceń hipotezy. Zbiór W' nazywamy zbiorem przyjęć. Weryfikując daną hipotezę statystyczną w oparciu o zaobserwowane wyniki próbki, ponosimy zawsze pewne ryzyko podjęcia błędnej decyzji. Wynika to stąd, że na podstawie próbki nigdy nie mamy całkowitej informacji o zbiorowości, z której pobrano próbkę. W wyniku testowania hipotezy statystycznej możemy więc podjąć poprawną decyzję lub popełnić jeden z dwu następujących błędów:

1. możemy odrzucić hipotezę H₀ wtedy, gdy jest ona w rzeczywistości prawdziwa

(błąd I rodzaju)

2. możemy przyjąć weryfikowaną hipotezę H₀ jako prawdziwą, gdy jest ona fałszywa, czyli

prawdziwa jest hipoteza alternatywna (błąd II rodzaju).

Prawdopodobieństwo popełnienia błędu I rodzaju to poziom istotności, oznaczany α; prawdopodobieństwo popełnienia błędu II rodzaju oznaczamy β. Wskazane jest, by prawdopodobieństwo błędów obu rodzajów uczynić możliwie małymi. Nie można jednak zmniejszać jednocześnie obu rodzajów błędów przy ustalonej liczności próby.

Błąd pierwszego rodzaju - w statystyce pojęcie z zakresu weryfikacji hipotez statystycznych - błąd polegający na odrzuceniu hipotezy zerowej, która w rzeczywistości jest prawdziwa. Błąd pierwszego rodzaju znany też jest jako: błąd pierwszego typu, błąd przyjęcia lub alfa-błąd.

Oszacowanie prawdopodobieństwo popełnienia błędu pierwszego rodzaju oznaczamy symbolem α (mała grecka litera alfa) i nazywamy poziomem istotności testu.

Błąd drugiego rodzaju (błąd drugiego typu, błąd przyjęcia, beta-błąd) - w statystyce pojęcie z zakresu weryfikacji hipotez statystycznych - polegające na nieodrzuceniu hipotezy zerowej, która jest w rzeczywistości fałszywa.

Oszacowanie prawdopodobieństwo popełnienia błędu drugiego rodzaju oznaczamy symbolem β (mała grecka litera beta) i nazywane jest mocą testu.

8. Parametryczne testy istotności. Weryfikacja hipotezy dotycząca wartości średniej, testy

istotności dla wariancji.

Weryfikacją hipotezy nazywamy sprawdzenie sądów o populacji, sformułowanych bez zbadania jej całości.

Weryfikacja hipotez dotycząca wartości średniej (wykład z 7.01.2006)

MODEL I

Badana cecha X populacji generalnej ma rozkład N(m, σ), gdzie σ >0 jest znane.

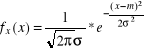
E(X)=m, D²(X)= σ²

Weryfikujemy hipotezę H₀:m=m₀ wobec hipotezy alternatywnej

1. H₁:m=m₁ < m₀

2. H₁:m=m₁ > m₀

3. H₁:m=m₁ ≠ m₀

Poziom istotności α, 0<α<1

Do weryfikacji hipotezy H₀ użyjemy statystyki
, która przy założeniu prawdziwości hipotezy H₀:m=m₀ ma rozkład N(0,1)

Postać zbioru krytycznego zależy od postaci hipotezy alternatywnej

a) jeżeli H₁:m=m₁ < m₀

to zbiorem krytycznym W jest przedział (-∞ ),u(α)}, gdzie u(α) jest kwantylem rzędu α rozkładu N(0,1)

konstrukcja testu do weryfikacji hipotezy H₀:m=m₀ wobec hipotezy alternatywnej H₁:m=m₁ < m₀ na poziomie istotności α

b) H₁:m=m₁ > m₀

to zbiorem krytycznym W jest przedział [(1-α), +∞), gdzie u(1-α) jest kwantylem rzędu 1-α rozkładu N(0,1)

Wykres...

c) jeżeli H₁:m=m₁ ≠ m₀ to zbiorem krytycznym W jest suma mnogościowa przedziałów (-∞, - u(1-α/2)] ∪[(1- α/2) +∞)

Wykres....

Jeśli wartość statystyki U jest obliczana dla próbki u_obl należy do zbioru krytycznego W to weryfikowaną hipotezę H₀ odrzucamy a przyjmujemy hipotezę alternatywną H₁. W przeciwnym przypadku nie ma podstaw do odrzucenia weryfikowanej hipotezy H₀.

Przyklad

Z populacji w której badana cecha X ma rozkład normalny X ~N(m,4) wylosowano próbkę o liczności n=9. Na poziomie istotności α=0,05 zweryfikować hipotezę H₀: m=2 wobec hipotezy H₁m=m₁ < 2 jesli średnia z próbki wynosi
=1,4

H_1:m=m₁ < m₀=2 to zbiór krytyczny W=(-∞, -u(1- )]=(-∞,-u(0,95)]= (-∞,-1,64] (1,64 z tablic)

MODEL II

Badana cecha X populacji generalnej ma rozkład N(m, σ), gdzie m, σ nieznane.

Weryfikujemy hipotezę H₀:m=m₀ wobec hipotezy alternatywnej

a) H₁:m=m₁ ≠ m₀

b) H₁:m=m₁ > m₀

c)H₁:m=m₁ < m₀

Poziom istotności α, 0<α<1

Do weryfikacji hipotezy H₀ użyjemy statystyki
, która przy prawdziwości hipotezy H₀:m=m₀ ma rozkład t-Studenta z n-1 stopniami swobody.

b) jeśli H₁:m₁ > m₀ to zbiorem krytycznym jest przedział [t(1-, n-1), +∞), gdzie t(1-, n-1) jest kwantylem rzędu 1-α rozkładu t-Studenta z n-1 stopniami swobody

c) jeśli H₁:m₁ < m₀ to zbiorem krytycznym jest przedział (-∞, - t(1-, n-1)]

a) jeśli H₁:m₁ ≠ m₀ to zbiorem krytycznym jest suma mnogościowa przedziałów (-∞, - t(1- /2, n-1)]∪[ t(1- /2, n-1), +∞), gdzie t(1- /2, n-1) jest kwantylem rzędu 1- /2 rozkładu
t- Studenta z n-1 stopniami swobody.

Jeśli wartość t_obl statystyki t obliczona dla danej próbki należy do zbioru krytycznego W wtedy weryfikowaną hipotezę H₀ odrzucamy na korzyść hipotezy alternatywnej H₁. W przeciwnym przypadku nie ma podstaw do odrzucenia weryfikowanej hipotezy H₀.

Testy istotności dla wariancji

Niech badana cecha X populacji generalnej ma rozkład N(m, σ), gdzie m, σ nieznane.

Weryfikujemy hipotezę H₀:σ ² =σ²₀ wobec hipotezy alternatywnej

a) H₁: σ ² =σ²₁ ≠σ ²₀

b) H₁: σ ² =σ²₁ > σ ²₀

c)H₁: σ ² =σ²₁ < σ ²₀

Poziom istotności α, 0<α<1, n≤50

Do weryfikacji hipotezy H₀ użyjemy statystyki
, która przy prawdziwości hipotezy H₀ :σ ² =σ²₀ ma rozkład χ² z (n-1) stopniami swobody.

b)Jeśli H₁: σ ² =σ²₁ > σ ²₀ to zbiorem krytycznym W jest przedział [χ²(1-α, n-1), +∞)
gdzie χ²(1-α, n-1) jest kwantylem rzędu 1-α z n-1 stopniami swobody

Wykres...

[χ²(1-α, n-1)

(zbiór krytyczny z prawej strony wykresu

W

Jeśli H₁: σ ² =σ²_{1 <} σ ²₀ to W (0, χ²(α, n-1)

Wykres...

Jeśli H₁: σ ² =σ²₁ ≠σ ²₀ to W (0, (1/2α, n-1)] ∪ [(1-1/2α, n-1), +∞)

Jeśli obliczona z próbki wartość statystyki
należy do zbioru krytycznego W to weryfikowaną hipotezę H₀ odrzucamy i przyjmujemy hipotezę alternatywną. W przeciwnym przypadku nie ma podstaw do jej odrzucenia.

UWAGA

Ponieważ tablice rozkładu χ² podają wartości kwantyli dla n≤50 to rozpatrzony model stosujemy przy założeniu, że próbka jest o liczności n≤50

Przykład

W celu oszacowania dokładności pomiaru wykonanych pewnym przyrządem dokonano n=8 pomiarów i otrzymano następujące wyniki: 18,17; 19,21; 18,05; 18,14; 18,19; 18,22; 18,06; 18,08;

α=0,05 H₀; σ ² =σ²₀ przeciw hipotezie alternatywnej:

a) H₁: σ ² =σ²₁ ≠σ ²₀

b) H₁: σ ² =σ²_{1 >} σ ²₀

c)H₁: σ ² =σ²_{1 <} σ ²₀

Poziom istotności α, 0<α<1, n>50

Do weryfikacji hipotezy H₀ wykorzystamy jak w poprzednim modelu statystykę
oraz fakt, że statystyka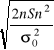
ma w przybliżeniu rozkład N(
, 1)

Do weryfikacji H₀ użyjemy statystyki
, która ma w przybliżeniu rozkład N(0,1)

1) jeśli H₁: σ ² =σ²_{1 >} σ ²₀ to zbiorem krytycznym W jest przedział [u(1-α), +∞), gdzie u(1-α) jest kwantylem rzędu 1-α rozkładu N(0,1)

2) jeśli H₁: σ ² =σ²_{1 <} σ ²₀ to zbiorem krytycznym W jest przedział (-∞, - u(1-α)]

3) jeśli H₁: σ ² =σ²₁ ≠σ ²₀ to zbiorem krytycznym W jest przedział ((-∞, - u(1-α/2)]∪[ u(1-α/2), +∞)

1

---