Ekonometria studia stacjonarne Wydział Zarządzania

Ćwiczenia 10: Analiza sezonowości z wykorzystaniem zmiennych 0-1. Zmienne jakościowe w modelu ekonometrycznym.

Model dla danych kwartalnych z uwzględnieniem zmiennych 0-1 ma postać:

(1)

,
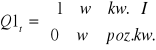
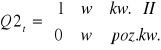
, itd.

Macierz obserwacji na zmiennych objaśniających, (przy założeniu, że ostatnia obserwacja pochodzi z IV kwartału) kształtuje się następująco:

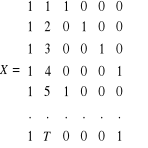
Ze względu na dokładną współliniowość zmiennych objaśniających modelu r(X)=5 (zamiast 6) i
, w związku, z czym oszacowanie jego parametrów strukturalnych metodą najmniejszych kwadratów nie jest możliwe.

Stosujemy następującą transformację zmiennych sezonowych:

I. Założenie: suma efektów sezonowych w ciągu całego roku musi się znosi i wynosi zero czyli:
, np.:
.

np.:

(Można również od zmiennych Q1, Q3, Q4 odjąć Q2, lub od Q2, Q3, Q4 odjąć Q1, itp.)

Model z tak zdefiniowanymi zmiennymi ma postać:

(2)

Macierz obserwacji na zmiennych objaśniających modelu (2) jest następująca:

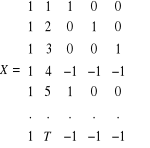
Jeśli T>=5, r(X)=5 to do oszacowania parametrów strukturalnych modelu (2) można zastosować KMNK.

Z powyższego zapisu wynika, że parametry stojące przy transformowanych zmiennych sezonowych w modelu (2) są identyczne z parametrami modelu wyjściowego i mają bezpośrednią interpretację jako efekty sezonowe w kwartałach I, II i III:

Efekt sezonowy w kwartale IV uzyskujemy jako:
, co wynika również z warunku, że efekty sezonowe w ciągu roku kompensują się.

informuje o efektach sezonowych w poszczególnych kwartałach w stosunku do średniego poziomu zjawiska.

II. Usuwa się jedną ze zmiennych 0-1 np.

(3)

Macierz obserwacji na zmiennych objaśniających modelu (3) jest następująca:

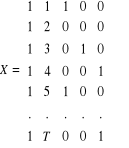
informuje o efektach sezonowych w i-tym kwartale w stosunku do okresu, który został pominięty w modelu.

Zadanie 1.

Oszacowany model ma postać:

przewozy kolejowe pasażerów w mln osób.

.

Polecenia:

1. Zinterpretuj wyniki oszacowania.

2. Zapisz model w postaci pierwotnej.

3. Zapisz macierz X dla modelu pierwotnego i oszacowanego.

4. Jakiej wielkości przewozów należy się spodziewać w okresie 50 - tym.

Zadanie 2

Na podstawie danych półrocznych pochodzących z 9 lat oszacowano następujący modle:

produkcja mleka w litrach.

.

Polecenia:

1. Zinterpretuj wyniki oszacowania.

2. Zapisz macierz obserwacji na zmiennych objaśniających tego modelu.

3. Zapisz wartości teoretyczne dla dwóch ostatnich lat.

Zadanie 3

Oszacowano postać modelu tendencji rozwojowej na podstawie danych z okresu 1993 Q1-1999Q4:

przewozy osób w tys.

1. Zinterpretuj wyniki oszacowania (tendencję i efekty sezonowe).

2. Oblicz wartość teoretyczną przewozów dla okresu t=15.

3. Zapisz macierz X, która posłużyła do oszacowania tego modelu.

Zadanie 4

Na podstawie danych kwartalnych za okres 1996Q3 - 1999Q3 oszacowano model:

kwartalne zużycie energii elektrycznej w kWh.

1. Oblicz efekt sezonowy dla IV kwartałów, podaj interpretację.

2. Wyznacz teoretyczną wartość zużycia energii elektrycznej w I kwartale 1998r.

3. Zaprognozuj teoretyczną wartość zużycia energii elektrycznej w IV kwartale 2000r.

Zadanie 5

Na podstawie danych miesięcznych z lat 2005-2008 produkcji masła w tys. ton oszacowano model:

1. Oblicz efekt sezonowy dla XII 2007 r., podaj interpretację.

2. Wyznacz teoretyczną wartość produkcji masła w VI 2008 r.

3. Zaprognozuj teoretyczną wartość produkcji masła w III 2009 r.

Zadanie 6

Na podstawie danych dotyczących kwartalnego zużycia energii elektrycznej (w MW) w firmie produkcyjno-usługowej „Pako” w latach 2005-2007:

Kwartały	Lata
		2005	2006	2007
I	2,8	3,0	3,5
II	3,7	4,2	4,7
III	3,0	3,5	4,0
IV	4,6	5,0	5,3

oszacowano parametry liniowej funkcji trendu:

1. Wyznacz wskaźniki sezonowości.

2. Zinterpretuj otrzymane wyniki.

3. Wyznacz teoretyczną wartość zużytej energii elektrycznej w III kwartale 2007 r.

Przejście do średniego poziomu zjawiska:

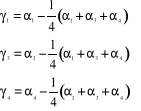
19

---