Nr ćwiczenia: 17	Temat ćwiczenia: Badanie pola magnetycznego za pomocą hallotronu	Wydział: FTiMK	Data: 10.10.2000
Zespół nr: 4	Imię i nazwisko: Elżbieta Pojnar	Rok: II	Ocena:

W 1879r. E. H. Hall odkrył ciekawe zjawisko dotyczące sił działających na nośniki prądu w polu magnetycznym. Zjawisko to zostało nazwane później zjawiskiem Halla.

Jeżeli przez jednorodny przewodnik płynie prąd elektryczny i przewodnik ten umieścimy w polu magnetycznym prostopadłym do kierunku prądu, to między dwoma punktami A i B, leżącymi naprzeciwko siebie po obu stronach przewodnika, pojawia się napięcie elektryczne wykrywalne woltomierzem. Napięcie to nazywamy napięciem Halla. Znak tego napięcia zmieni się, jeśli zmienimy kierunek prądu I, lub kierunek pola magnetycznego B. Napięcie Halla jest proporcjonalne do wartości indukcji magnetycznej B

i natężenia prądu I.

Napięcie Halla jest związane bezpośrednio z obecnością pola magnetycznego i jego wpływem na nośniki prądu.

Nośniki prądu w próbce przewodzącej (elektrony) można uważać za swobodne. Załóżmy, że w przypadku nieobecności pola magnetycznego wszystkie elektrony poruszają się ze średnią prędkością unoszenia
w kierunku przeciwnym do pola elektrycznego E
. Po włączeniu pola magnetycznego na nośniki prądu będzie działać siła Lorentza o wartości:

skierowana prostopadle do ich prędkości
i do wektora indukcji B. Siła ta jest odpowiedzialna za zakrzywienie toru cząstek. Wskutek tego na jednym boku próbki wytworzy się nadmiar elektronów i bok ten naładuje się ujemnie, a na przeciwnym boku pozostaną jony dodatnie. Powstanie pole elektryczne E
prostopadłe do kierunku przepływu prądu, a zatem pojawi się siła elektrostatyczna
skierowana przeciwnie do działania siły Lorentza. Siła elektrostatyczna będzie narastać, aż do momentu, kiedy zrówna się co do wartości z siłą Lorentza. Wówczas wpływ obu sił na znak nośników skompensuje się.

Po podzieleniu obu stron równania przez q otrzymujemy:

Pole elektrostatyczne jest związane z potencjałem Halla U
w następujący sposób:

Z definicji natężenia prądu mamy:

gdzie: n - ilość nośników w jednostce objętości próbki

S - pole powierzchni przekroju próbki

Wiemy, że
, zatem:

czyli:

Podstawiając wzory na E
oraz
do równania
otrzymamy:

Po obustronnym pomnożeniu przez d otrzymamy:

gdzie R
- stała Halla

Znak stałej Halla zależy od znaku nośników prądu. Gdy q = -e, R_H < 0. Jednak dla niektórych materiałów otrzymujemy dodatnią wartość R_H. Mamy wtedy do czynienia z anomalnym efektem Halla. Jest on tłumaczony obecnością dodatnich nośników prądu - dziur w próbce.

Ważnym parametrem jest równie ruchliwość nośników u. Jest to współczynnik proporcjonalności między wartościami prędkości nośników i natężenia pola elektrycznego w próbce:

W wielu ciałach występują zarówno elektrony jak i dziury. Fakt ten prowadzi do wzoru na stałą Halla:

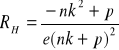
gdzie: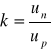
- stosunek ruchliwości elektronów do ruchliwości dziur

n - koncentracja elektronów

p - koncentracja dziur

Hallotron jest to urządzenie elektroniczne wykorzystywane przede wszystkim do wykrywania pola magnetycznego i pomiaru indukcji elektrycznej, zwłaszcza w maszynach elektrycznych.

Hallotron ma zastosowanie między innymi do:

• pomiaru natężeń silnych prądów stałych

• mocy prądów stałych, zmiennych i szybkozmiennych

• jako elementy komputerów

• w urządzeniach przekształcających prąd stały na zmienny

gdzie
- stała hallotronu.

Aby uzyskać dużą wartość stałej γ do wykonania hallotronów stosuje się cienkie warstwy z półprzewodników typu n naparowane na cienkie ceramiczne podłoże. W tym celu wykorzystuje się: german, krzem, antymonek indu, arsenek indu, tellurek rtęci. Hallotrony wykonywane z tego samego materiału nie zawsze mają identyczne parametry, dlatego każdy hallotron posiada indywidualną charakterystykę.

Trudno jest umieścić tak elektrody przy pomiarze napięcia Halla, aby znajdowały się w jednej powierzchni ekwipotencjalnej. W związku z tym, nawet w obecności pola magnetycznego, między tymi elektrodami istnieje pewne napięcie U_R zwane napięciem asymetrii, które jest proporcjonalne do natężenia zasilającego hallotron. Mierzone napięcie wynosi:

Metoda pomiaru:

Znając parametry geometryczne solenoidu oraz natężenie płynącego prądu I_S można stosunkowo łatwo obliczyć indukcję pola magnetycznego dla punktów leżących na jego osi, korzystając z prawa Biota - Savarta. Prowadzi to do wzoru:

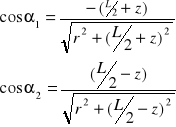
Dla z = 0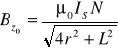
.

Wykonanie ćwiczenia:

1. Wyznaczam zależność napięcia Halla od natężenia prądu zasilającego hallotron U_H = f(I) w stałym polu magnetycznym. Otrzymane wyniki przedstawiam w poniższej tabelce:

Lp.	I [mA]	UR [mV]	U [mV]	UH = U- UR [mV]
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.	1,01 1,99 2,98 4,05 4,96 5,94 7,15 7,75 8,57 9,93	-0,099 -0,196 -0,292 -0,396 -0,483 -0,576 -0,690 -0,745 -0,820 -0,940	-0,097 -0,191 -0,284 -0,385 -0,470 -0,561 -0,671 -0,723 -0,796 -0,913	0,002 0,005 0,008 0,011 0,013 0,015 0,019 0,022 0,024 0,027

ΔI_H = 0,001[mA]

ΔU_H = 0,001[mV]

ΔU_R = 0,001[mV]

ΔU = 0,001[mV]

Korzystając z empirycznego współczynnika k obliczam wartość indukcji w środku solenoidu:

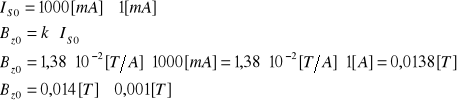
Wykres zależności U_H = f(I) dla B_z =B_z0=const. przedstawia rys.1.

2. Wyznaczam wartość napięcia Halla od natężenia prądu zasilającego solenoid oraz dla wartości I_S obliczam indukcję pola magnetycznego w środku solenoidu, korzystając ze wzoru:
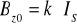
   . Otrzymane wyniki przedstawiam w tabelce:

I0 = 9,1[mA]		UR0 = -0,857[mV]		Bz0
Lp.	IS [mA]	U [mV]	UH = U - UR0 [mV]
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.	150 290 420 530 780 1000 1260 1480 1860 2000	-0,856 -0,852 -0,849 -0,845 -0,842 -0,837 -0,831 -0,826 -0,816 -0,810	0,001 0,005 0,008 0,012 0,015 0,020 0,026 0,031 0,041 0,047	2,070 4,002 5,796 7,314 10,764 13,800 17,388 20,424 25,668 27,600

ΔI_S = 1[mA]

ΔI₀ = 0,1[mA]

ΔU_R = 0,001[mV]

ΔU = 0,001[mV]

ΔU_H = 0,001[mV]

Wykres zależności
dla
przedstawia rys.2.

3. Wyznaczam zależność napięcia Halla od położenia hallotronu na osi solenoidu

U_H = f(z). Otrzymane wyniki pomiarów przedstawiam w tabelce:

I0 = 1000 [mA]		IS0 = 9,1[mA]		UR0 [mV]
Lp.	z [cm]	U [mV]	UH = U - UR0 [mV]
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.	0 -1 -2 -3 -4 -5 -6 -7 -8 +1 +2 +3 +4 +5 +6 +7 +8	-0,798 -0,807 -0,800 -0,801 -0,805 -0,808 -0,809 -0,811 -0,813 -0,807 -0,805 -0,797 -0,806 -0,807 -0,806 -0,806 -0,807	0,022 0,008 0,021 0,019 0,018 0,016 0,018 0,016 0,014 0,022 0,022 0,030 0,020 0,020 0,020 0,019 0,017	-0,820 -0,815 -0,821 -0,820 -0,823 -0,826 -0,827 -0,827 -0,827 -0,829 -0,827 -0,827 -0,826 -0,827 -0,826 -0,825 -0,824

h

I

B

I

-

L

z

r

y

z

---