Nr ćwicz. 103 |
Data
|
|
Wydział
|
Semestr
|
Grupa
|
Prowadzący:
|
Przygotowanie |
Wykonanie |
Ocena |
||
Wyznaczanie modułu Younga metodą wydłużenia
Wstęp teoretyczny
Atomy, z których składa się każde ciało stałe, oddziaływują ze sobą siłami zależnymi od wzajemnej odległości. Przy pewnej odległości ro siła działająca między atomami jest równa zeru, a energia potencjalna osiąga wartość minimalną. Jest to odległość, przy której atomy są w równowadze. Gdy w ciele stałym wszystkie atomy znajdują się względem siebie w odległościach równowagowych, wówczas ciało to jest w równowadze - nie dąży samorzutnie do zmiany wymiarów.
Jeżeli odległość między atomami będzie zmieniona, np. wskutek działania siły zewnętrznej, pojawi się siła sprężystości, która działa zawsze w takim kierunku, aby przywrócić stan równowagi. Przy zwiększeniu odległości powyżej ro, siła ma wartość ujemną (atomy się przyciągają), natomiast gdy odległość jest mniejsza od ro, znak siły jest dodatni, co oznacza, że atomy się odpychają.
Ze zmianą odległości wzajemnej atomów wiąże się makroskopowa deformacja ciała zwana odkształceniem. Gdy odkształcenie znika po odjęciu siły zewnętrznej, nazywamy je sprężystym, natomiast odkształcenie nie znikające po odjęciu siły nazywamy plastycznym.
Siły odkształcające mogą działać prostopadle lub stycznie do powierzchni. Stosunek siły normalnej (prostopadłej) (Fn) do wartości powierzchni (S), na którą działa nazywamy naprężeniem normalnym:
![]()
Pod wpływem naprężeń normalnych ciało ulega wydłużeniu lub skróceniu. Stosunek przyrostu długości (Δl) do długości początkowej (l) nazywamy odkształceniem względnym.
![]()
Wydłużenie względne jest wprost proporcjonalne do naprężenia normalnego:
![]()
Powyższe stwierdzenie stanowi treść prawa Hooke'a i pozostaje słuszne zarówno dla odkształcenia dodatniego (wydłużenia), jak i ujemnego (skrócenia). Współczynnik proporcjonalności E nazywamy modułem Younga. Ma on wymiar ciśnienia (naprężenia) - w układzie SI - N/m2. Z powyższego równania wynika sens fizyczny modułu Younga - jest to wielkość naprężenia potrzebna do wydłużenia ciała o długość początkową. Określenia tego na ogół nie można wykorzystać do wyznaczenia modułu Younga, ponieważ dla większości ciał granica stosowania prawa Hooke'a leży znacznie poniżej wartości modułu Younga.
W celu wytyczenia sposobu wyznaczania modułu Younga napiszmy omawiane równanie w postaci bardziej rozwiniętej:
![]()
Jeżeli na osiach układu współrzędnych odłożymy: stosunek siły do powierzchni przekroju oraz wydłużenie względne, to wykresem tego równania będzie linia prosta, której współczynnik nachylenia jest modułem Younga.
Opis ćwiczenia
Ćwiczenie przeprowadzałem dla drutu, którego wymiary zostaną omówione w dalszej części sprawozdania. Pierwszym etapem ćwiczenia było zmierzenie długości i średnicy drutu. W drugim etapie ćwiczenia do obciążenia podstawowego, mającego za zadanie wyeliminować wszelkie zagięcia drutu, dokładałem kolejno odważniki, w celu zwiększenia działającej na drut siły rozciągającej F, mierząc każdorazowo przyrost długość drutu. Po dotarciu do maksymalnego obciążenia (wykorzystaniu wszystkich ciężarków) zdejmowałem stopniowo obciążenie, również mierząc przyrosty (tym razem ujemne) długości drutu.
Schemat ćwiczenia
Pomiar długości drutu
Pomiar średnicy drutu i obliczenie pola powierzchni przekroju
Pomiar przyrostów długości drutu dla rosnących sił rozciągających
Pomiar przyrostów długości drutu dla malejących sił rozciągających
Obliczenie naprężeń normalnych drutu σ oraz odkształceń względnych ε dla wszystkich obciążeń
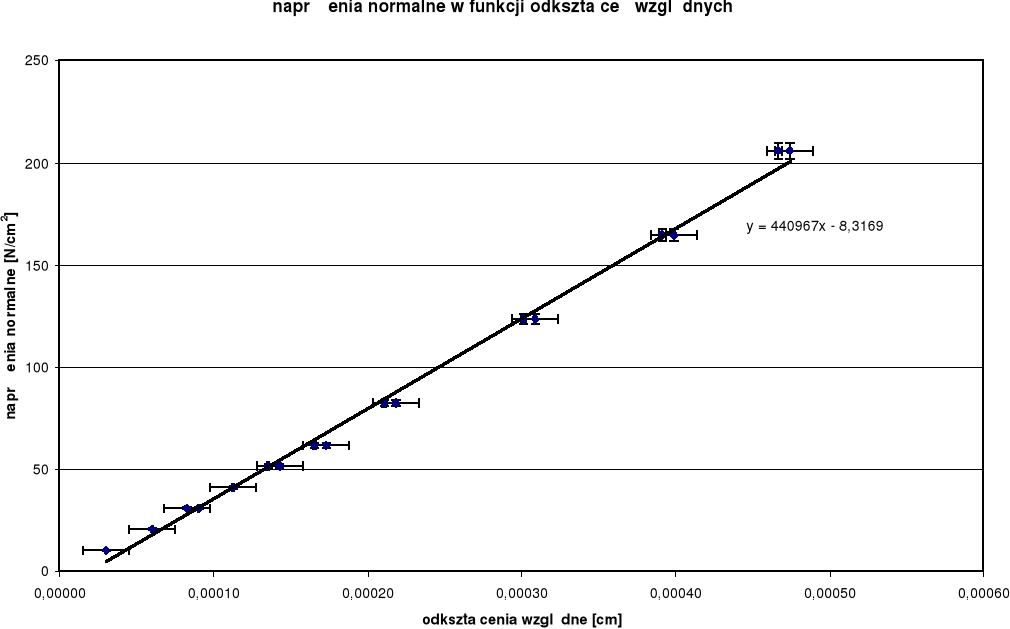
Sporządzenie wykresu naprężeń normalnych w funkcji odkształceń względnych i odczytanie metodą regresji liniowej modułu Younga
Dane eksperymentalne
Pomiar długości drutu
l = 132,80 cm
Pomiary średnicy drutu
Wskazania śruby mikrometrycznej dla rosnących i malejących obciążeń (w [cm])
Obliczenie wyników i dyskusja błędów
Błędy systematyczne
Obliczenie średniej średnicy drutu i pola powierzchni przekroju (w [cm])
Obliczenie naprężeń normalnych drutu σ oraz odkształceń względnych ε dla wszystkich obciążeń
Obliczenie odkształceń względnych ε
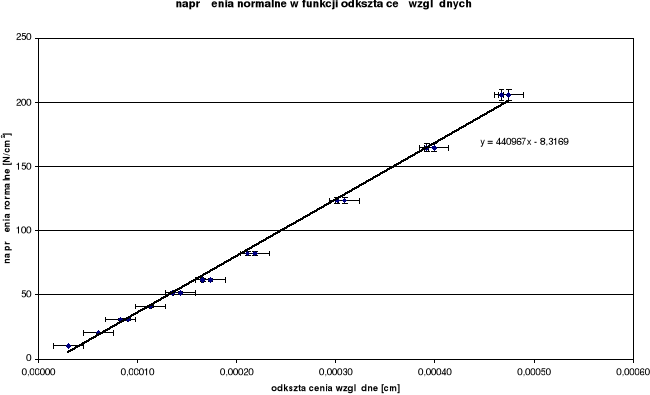
Sporządzenie wykresu naprężeń normalnych w funkcji odkształceń względnych i odczytanie metodą regresji liniowej modułu YoungaZestawienie wyników
Wnioski końcowe
pomiar |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
średnica drutu |
0,049 |
0,048 |
0,048 |
0,049 |
0,047 |
0,048 |
0,047 |
0,048 |
0,047 |
0,046 |
Pomiar 1 |
|
Pomiar 2 |
|
wskaz zerowy |
0,453 |
masa ciężarków (kg) |
wskazania |
masa ciężarków (kg) |
wskazania |
1,00 |
0,516 |
0,05 |
0,457 |
0,80 |
0,506 |
0,10 |
0,461 |
0,60 |
0,494 |
0,15 |
0,464 |
0,40 |
0,482 |
0,20 |
0,468 |
0,30 |
0,476 |
0,25 |
0,472 |
0,25 |
0,472 |
0,30 |
0,476 |
0,20 |
0,469 |
0,40 |
0,482 |
0,15 |
0,466 |
0,60 |
0,494 |
0,10 |
0,462 |
0,80 |
0,506 |
0,05 |
0,458 |
1,00 |
0,516wskaz zerowy |
wskaz zerowy |
0,454 |
Błędem wynikającym z klasy przyrządów obarczony był pomiar długości drutu (± 0,1 cm) oraz każdy pomiar średnicy drutu i zmiany wydłużenia (± 0,001 cm). Masę ciężarków, w związku z brakiem oznaczeń dokładności, przyjąłem za idealną.
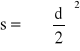
średnica d |
błąd |
0,048 |
± 0,001 |
Obliczenie błędu Δs metodą różniczki logarytmicznej:
![]()
,
stąd s = 0,002 cm2 ± 0,0002 cm
Naprężenia liczymy ze wzoru ![]()
, co po zastosowaniu metody różniczki logarytmicznej daje błąd ![]()
. Jednostką jest ![]()
|
|
|
g |
9,81 |
|
|
naprężenia normalne |
błąd |
|
naprężenia normalne |
błąd |
1 |
10,283 |
±0,194 |
11 |
205,660 |
±3,880 |
2 |
20,566 |
±0,388 |
12 |
164,528 |
±3,104 |
3 |
30,849 |
±0,582 |
13 |
123,396 |
±2,328 |
4 |
41,132 |
±0,776 |
14 |
82,264 |
±1,552 |
5 |
51,415 |
±0,970 |
15 |
61,698 |
±1,164 |
6 |
61,698 |
±1,164 |
16 |
51,415 |
±0,970 |
7 |
82,264 |
±1,552 |
17 |
41,132 |
±0,776 |
8 |
123,396 |
±2,328 |
18 |
30,849 |
±0,582 |
9 |
164,528 |
±3,104 |
19 |
20,566 |
±0,388 |
10 |
205,660 |
±3,880 |
20 |
10,283 |
±0,194 |
Odkształcenia względne liczymy ze wzoru ![]()
, gdzie Δl jest przyrostem długości drutu. Tutaj wzór ten przyjmie postać ![]()
, gdzie z jest wskazaniem śruby mikrometrycznej dla konkretnego obciążenia, a z0 jest wskazem zerowym. Błąd obliczeń znajdujemy metodą różniczki logarytmicznej: 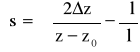
, jednostkami są centymetry.
|
odkształcenia względne |
błąd |
|
odkształcenia względne |
błąd |
1 |
0,00003 |
±0,0000150 |
11 |
0,00047 |
±0,0000024 |
2 |
0,00006 |
±0,0000150 |
12 |
0,00039 |
±0,0000020 |
3 |
0,00008 |
±0,0000150 |
13 |
0,00030 |
±0,0000016 |
4 |
0,00011 |
±0,0000150 |
14 |
0,00021 |
±0,0000011 |
5 |
0,00014 |
±0,0000150 |
15 |
0,00017 |
±0,0000009 |
6 |
0,00017 |
±0,0000149 |
16 |
0,00014 |
±0,0000007 |
7 |
0,00022 |
±0,0000149 |
17 |
0,00011 |
±0,0000006 |
8 |
0,00031 |
±0,0000148 |
18 |
0,00009 |
±0,0000005 |
9 |
0,00040 |
±0,0000148 |
19 |
0,00006 |
±0,0000003 |
10 |
0,00047 |
±0,0000147 |
20 |
0,00003 |
±0,0000002 |
Z wykresu odczytujemy, że moduł Younga dla badanego drutu ma wartość 440967 N/cm2, czyli z dużym przybliżeniem 44,1 N/m2.
Dla obydwu pomiarów wartości wskazań śruby mikrometrycznej pokrywały się dopiero od pewnego momentu (obciążenia powyżej 200 gram), co wskazuje na zbyt małą wartość masy kontrolnej, odpowiedzialnej za wyprostowanie i wstępne naciągnięcie drutu. Pomiary przebiegały prawidłowo, wyniki pomiarów mieściły się w granicach obliczonych błędów.
laboratorium mechaniczne sprawozdanie z ćw. nr 103 strona nr 1
Wyszukiwarka
Podobne podstrony:
mech 1, WNOŻCiK wieczorowe, semestr I, fizyka
sila termoelektryczna, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania),
OS-zagadnienia, Semestr 1, Fizyka
Zal-lab-BP-zaoczne, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
przykładowe pytania, studia MEiL, semestr 2mgr, semestr 9, fizyka 2
Fizyka proj 3, Budownictwo UTP, semestr 3, Fizyka Budowli
Fifyka komputerowa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Wydział Inżynierii Elektrycznej i Komputerowej 02, studia, PK - WIŚ -UCZ, Semestr I, Fizyka
Metodyka rozwiązywania zadań, Transport Politechnika, Semestr 1, Fizyka
Elektronika 03, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
39, Semestr 1, Fizyka
kationy, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
kolokwium 14 01 10, polibuda, 3 semestr, fizyka i inżynieria materiałowa (kolokwia, sprawozdania, w
test-B, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
Laboratorium sprawozdania cz. 3, Mechanika III semestr, Fizyka, Laboratoria i sprawozdania
308t, Polibuda, II semestr, Fizyka laboratoria, Fizyka- laboratoria, Laborki- inne2
więcej podobnych podstron