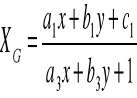
TRANSFORMACJA RZUTOWA

Transformacja rzutowa to ośmioparametrowe przekształcenie płaszczyzny zdjęcia na powierzchnię terenu. W parametrach transformacji zawarte są elementy orientacji zewnętrznej i wewnętrznej za wyjątkiem dystorsji. Proces transformacji polega na tym iż najpierw definiujemy punkt główny, poprawiamy piksele o współczynniki radialne i obraz skorygowany o dystorsję radialną przekształcamy rzutowo. Po transformacji zmienia się poziom szarości pikseli. W resamplingu szukamy nowych poziomów szarości.

Ogólne wzory transformacji rzutowej:

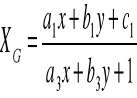
X_G , Y_G - współrzędne geodezyjne

x, y - współrzędne w układzie zdjęcia

Podczas zajęć dydaktycznych korzystano zdjęć archiwalnych z 1978 r. zrobionych przez PPGK W-wa dla obiektu Ciechanów. Pracowano na prawym zdjęciu.

Przebieg pracy:

1. Założenie folderu 2D

2. Stworzenie pliku z rozszerzeniem *pkt zawierającego punkty osnowy fotogrametrycznej

3. Uruchomienie programu VSD

- nazwa zadania taka jak numer prawego zdjęcia

- wpisanie ścieżki dostępu do obrazu zdjęcia

- stworzenie pliku z obrazem piramidalnym

- pomiar fotopunktów klawiszem „i” - podpięcie z pliku *pkt

- orientacja wewnętrzna zdjęcia, określenie transformacji - F5

- pomiar narożników użytków klawiszem ”j”

4. Opracowanie wyników pomiarów

STEREODIGITALIZACJA

Stereodigitalizacja to proces pozyskiwania danych geometrycznych o obiektach. Dla wykonania stereodigitalizacji wykonuje się rekonstrukcję modelu przestrzennego terenu na podstawie pary zdjęć na autografie analogowym, analitycznym lub cyfrowym, a następnie poprzez interpretację i pomiar określa się lokalizacje wybranych obiektów w zewnętrznym układzie odniesienia. Technika pomiaru sprowadza się do pomiarów punktów i linii. pomiar punktowy to pomiar punktów dyskretnych a pomiar liniowy to pomiar ciągły. Tryb pomiarów punktowych to tryb statyczny.

Tego typu pomiar prowadzi do prezentacji każdego mierzonego obiektu w zapisie numerycznym przyporządkowując go do jednego z podstawowych typów czyli:

- obiektu punktowego - prezentacja symboliczna z prawidłową lokalizacją centrum zastosowanego symbolu,

- obiektu liniowego - prezentacja ciągiem poli-linii otwartej lub zamkniętej kartometrycznie lokalizującej prezentowany obiekt,

- obiektu powierzchniowego - obszar zamknięty ciągiem liniowym z przyporządkowanym sposobem użytkowania wydzielonego obszaru.

Grupy obiektów na etapie mapy numerycznej metodą stereodigitalizacji:

1. Pomiar punktów

2. Pomiar linii przestrzennych w sposób dynamiczny; zmieniają się współrzędne X, Y, Z

3. pomiar linii wysokości(warstwic); zmienia się X, Y a współrzędna Z musi być przez operatora utrzymywana na stałej wysokości

4. Dynamiczny sposób pomiaru profilami; dla dowolnie zorientowanego profilu ΔX ≠ΔY , współrzędna Z jest zmienna.

W przypadku pomiarów statycznych może zaistnieć sytuacja gdy stosujemy metodę siatki kwadratów ze względu na bezproblemowe zdefiniowanie punktów węzłowych siatki. Taki pomiar rastra jest alternatywą dla pomiarów warstwami i pozwala uzyskać większą dokładność. Dla niewielkich obszarów DGM -u stosujemy metodę punktów rozproszonych

Stosowane oprogramowanie pozwala w procesie pomiaru nadawanie dodatkowo automatycznie poszczególnym obiektom oryginalnych kodów gwarantując w ten sposób niezbędną niezawodność pomiaru, a następnie efektywne tworzenie lub aktualizację baz danych systemu GIS.

Do wykonania stereodigitalizacji zdjęć lotniczych na instrumentach fotogrametrycznych można wykorzystywać bezpośrednio oprogramowanie, w którym docelowo będzie prowadzony system informacji przestrzennej ( np. MICROSTATION, ARC-INFO) co znacznie ułatwia transfer danych i zakładanie lub aktualizację bazy danych w systemie.

Proces stereodigitalizacji prowadzony nawet w najnowszych instrumentach typu autograf cyfrowy jest zawsze realizowany przez operatora(obserwatora) i w najbliższym czasie nie będzie zautomatyzowany( w przyszłości obserwatora zastąpi pakiet programowy do komputerowego rozpoznawania obiektów).

Efektywne wykonanie procesu aktualizacji wymaga nakładania istniejącej zawartości bazy geometrycznej(mapy numerycznej) na modele fotogrametryczne utworzone z aktualnych zdjęć lotniczych. Taka superimpozycja obrazów pozwala na jednoznaczne wykrywanie zmian oraz kompleksowe prowadzenie procesu aktualizacji. Realizacja nakładania różnej treści danych numerycznych i cyfrowych odbywa się automatycznie jedynie w systemach cyfrowych. To zadanie w autografach analitycznych jest wykonywane sprzętowo( np. w autografach firmy Zeiss przy pomocy Videomapu) i wymaga dodatkowych zakupów i konfigurowania sprzętu.

Końcowym wynikiem stereodigitalizacji jest mapa wektorowa a jej ostateczna redakcja jest uzależniona od skali mapy, która analogowo będzie dostępna.

Podczas zajęć dydaktycznych dokonano stereodigitalizacji w VSD w trybie punktowym, statycznym. Ustawiano znaczek pomiarowy na wybranych punktach modelu i dokonano pomiar obiektu. W przypadku pomiaru punktowego rejestrowano współrzędne klawiszem „j”. Ruch wysokościowy znaczka uzyskiwano dzięki klawiszom F1 i F2 natomiast ruch w płaszczyźnie XY za pomocą myszy. Pomiar wektora za pomocą klawisza „P”. Zdefiniowano trzy warstwy na których pracowano:

1. budynki

2. drogi

3. użytki

Wyniki stereodigitalizacji ,uzyskane dokładności oraz mapę sytuacyjną przedstawiono na kolejnych stronach sprawozdania.

METODA WIĄZEK

Podstawą metody wiązek jest warunek kolinearności. W metodzie tej wszystkie równania kolinearności możliwe do ułożenia dla całego bloku zdjąć układane są i rozwiązywane równocześnie. W metodzie tej elementy orientacji wszystkich zdjęć bloku oraz nieznane współrzędne wyznaczonych punktów terenowych oblicza się równocześnie ze wszystkich dających się wykorzystać danych i nie dzieli się procesu aerotriangulacji na etapy. Warunkiem przecięć promieni homologicznych jest uzupełniony warunkiem przejścia promieni przez punkt o danych współrzędnych terenowych.

Współrzędne fotopunktów (Xw, Yw, Zw) traktowane są jako znane i bezbłędne lub jako dane obarczone błędami. Niewiadomymi są wszystkie parametry zdjęć bloku oraz współrzędne fotopunktów, np. współrzędne Z, kiedy znane są Xw, Yw lub współrzędne X i Y, kiedy znana jest wysokość Zw). Liczbę wszystkich niewiadomych dla danego bloku można określić mnożąc liczbę zdjęć przez liczbę parametrów każdego zdjęcia. Jeśli przyjmie się stałość elementów orientacji wewnętrznej kamery, to wyznaczane parametry będą związane tylko z elementami orientacji zewnętrznej stanowisk kamer, a więc liczba przez którą należy pomnożyć liczbę zdjęć wynosi 6. Obliczoną w taki sposób liczbę niewiadomych należy powiększyć o potrójną wartość punktów aerotriangulacyjnych, dla których wyznacza się współrzędne terenowe.

Wyrównanie metodą wiązek:

Standardowe wyrównanie metodą wiązek sieci zdjęć cyfrowych stanowi kombinowane wyrównanie obserwacji fotogrametrycznych i geodezyjnych. Wyznacza elementy orientacji przestrzennej zdjęć i współrzędne X,Y,Z punktów obiektu. W przypadku niedostatecznej dokładności wyznaczenia fotopunktów i innych obserwacji geodezyjnych lub ich braku stosuje się technikę swobodnego wyrównania sieci. Przy korzystnej konfiguracji zdjęć i dobrym uwarunkowaniu układu równań możliwe jest również jednoczesne określenie parametrów kalibracji kamery. Opcjonalna kalibracja zawiera wyznaczenie podstawowych elementów orientacji wewnętrznej c_K, x¢₀, y¢₀ kamery oraz dodatkowe parametry, które opisują błędy systematyczne obrazu. Ocenę wyników wyrównania przeprowadza się na podstawie analizy błędów i kryteriów dokładności. Typowa analiza obejmuje odchylenie standardowe Sigma 0, parametry wewnętrznej i zewnętrznej dokładności, parametry wewnętrznej i zewnętrznej wiarygodności. Szczególnie ważny jest test wykrywania i eliminacji błędów grubych obserwacji fotogrametrycznych, które spowodowane są najczęściej błędną identyfikacją punktów lub niedokładnością wyznaczenia punktów homologicznych na obrazach epipolarnych.

Dodatkowe punkty i zdefiniowane obiekty graficzne mogą być określone metodą fotogrametrycznego przestrzennego wcięcia w przód w oparciu o obliczone elementy orientacji zdjęć.

Program AeroSys

AeroSys służy do rozwiązania i wyrównania aerotriangulacji metodą wiązek. Parametry wejściowe to:

• pomierzone znaczki tłowe

• pomierzone punkty Grubera

• pomierzone fotopunkty

• pomierzone punkty nowo wyznaczane Na początku przygotowujemy pliki

• basename.txt - ze współrzędnymi Iłowymi w układzie pikselowym;

• basename.cal - zawierający dane o liczbie znaczków Iłowych , Ck, skalibrowane współrzędne punktu głównego, współrzędne dla określenia dystorsji radialnej i tangencjalnej;

• basename.bld - zawierający dane o liczbie zdjęć w szeregu, ilości kamer, Cp, ilości znaczków tłowych

• basename.ctl - zawierający współrzędne fotopunktów oraz ich dokładności. Wynikiem aerotriangulacji są:

• współrzędne geodezyjne wyrównane nowo wyznaczanych punktów

• oceny dokładności wyznaczenia tych punktów

• elementy orientacji zewnętrznej

• poprawki do obserwacji

VSD AGH

Video Stereo Digitizer AGH (VSD) jest analitycznym autografem cyfrowym przeznaczonym do opracowywania czarno białych lub kolorowych par cyfrowych obrazów fotogrametrycznych (stereogramów lub stereofotogramów).

VSD akceptuje skanowane obrazy lotnicze, naziemne jak i satelitarne, obrazy skanerowe, obrazy pochodzące z kamer CCD.

VSD może być używany do tworzenia lub aktualizacji numerycznych map topograficznych, tematycznych itp. Jak również do sporządzania wektorowej dokumentacji architektonicznej, konserwatorskiej lub archeologicznej.

Pary obrazów cyfrowych wyświetlonych na ekranie SVGA komputera typu PC obserwowane są przy pomocy stereoskopu zwierciadlanego. Szczegóły wybierane są przez operatora przy użyciu pary kursorów (znaczków pomiarowych) animowanych myszą. Wskazywane homologiczne punkty obu obrazów mogą być łączone linią łamaną. Nieregularne krzywe są wykreślane przez rejestrowanie trajektorii kursora. Linie łamane i trajektorie nakładane są na półtonalne obrazy cyfrowe na ekranie PC w wybranym kolorze. Każdy kolor linii lub trajektorii stanowi oddzielną warstwę w kodzie DXF lub kodzie binarnym programu VSD. Obserwowane pojedyncze punkty mogą być również zapisywane w plikach tekstowych lub w kodzie DXF dla potrzeb np. DTM lub tworzonej mapy numerycznej.

Z wykorzystaniem VSD możliwe jest opracowywanie wektorowe pojedynczych fotogramów cyfrowych obiektów płaskich (przetwarzanie analityczne).

VSD pracuje również w trybie mono lub stereokomparatora wykonując pomiar obrazów cyfrowych z dokładnością odpowiadającą ułamkom piksela zależną od skali powiększenia obrazu cyfrowego.

W miarę potrzeb VSD może być zatem: autografem, przetwornikiem analitycznym zwektoryzowanych obrazów, monokomparatorem lub stereokomparatorem.

Program VSD akceptuje następujące formaty obrazów cyfrowych:

1. TIFF monochromatyczny (maks.256 półtonów),

2. TIFF kolorowy, indeksowany, z paletą o 256 kolorach.

W trakcie wizualizacji pary barwnych obrazów w programie VSD palety obrazów zostają zsumowane a następnie zredukowane do 248 pozycji. Pozostałe 8 kolorów jest zarezerwowanych dla numerycznej mapy wektorowej wyświetlanej na ekranie oraz dla napisów pomocniczych. Pliki kolorowe RGB (True Color) muszą być przed wprowadzeniem do VSD przetworzone do formatu indeksowanego lub monochromatycznego, Odpowiednią konwersję można zrealizować przy użyciu dołączonego programu RGB_VSD.

Zarówno VSD, jak i wyżej wymienione programy narzędziowe do konwersji, obecnie nie akceptują obrazów, przy zapisie których zastosowano kompresję, natomiast obsługują zarówno obrazy zapisane tradycyjnie wierszami pikseli jak i obrazy zapisywane w formacie mozaiki prostokątów (tzw. Opcja Tiled, stosowana dla dużych plików obrazowych).

Po zgłoszeniu plików obrazowych do zadania VSD, program proponuje utworzenie plików z tzw. piramidami obrazów. W razie akceptacji tej propozycji powstają wieloobrazowe pliki formatu TIFF zawierające szeregi obrazów o rozdzielczościach redukowanych dwukrotnie względem poprzednika w szeregu. Ostatni obraz szeregu umieści się w całości na połowie ekranu. Pliki te umożliwiają opracowanie obrazów pomniejszonych na ekranie w stosunku do skali obrazów pierwotnych i wymagają dodatkowo pamięci dyskowej o rozmiarze ok.33% rozmiaru obrazów pierwotnych.

Organizacja pamięci dyskowej

Przed uruchomieniem programu należy utworzyć katalog dyskowy, zwany katalogiem roboczym VSD, któremu można nadać dowolną nazwę. W razie potrzeby obrazy cyfrowe mogą być umieszczone w dowolnych katalogach, a także na innych napędach dyskowych niż napęd katalogu roboczego. Pliki tekstowe przygotowane dla VSD, opisane poniżej, należy umieszczać w katalogu roboczym. W katalogu roboczym może być ulokowane jedno lub więcej tzw. zadań (projektów). Wszystkie pliki tworzące zadanie (poza plikami wynikowymi, plikami importowanymi oraz plikami zawierającymi wyniki orientacji) mają wspólną nazwę zgodną z nazwą zadania, uzupełnioną trzyliterowym rozszerzeniem określającym typ pliku.

Istniejące mapy wektorowe 2D i 3D w formacie DXF mogą być włączane do zadania po transformacji do formatu ABS, właściwego dla VSD. Taką transformację realizuje dołączony program narzędziowy DXF_ABS.EXE umożliwiając ponadto selekcję i modyfikację ich kolorów.

ORIENTACJA WEWNĘTRZNA ZDJĘĆ

Elementy orientacji wewnętrznej pozwalają na odtworzenie wiązki promieni rzucających. Są to elementy liniowe określające położenie środka rzutów S w stosunku do płaszczyzny obrazowej.

Elementami orientacji wewnętrznej zdjęcia są:

- odległość obrazowa kamery fotogrametrycznej oznaczona symbolem f lub Ck ( f = Ck ),

- współrzędne punktu głównego zdjęcia o (x, y) stanowiącego rzut prostokątny środka rzutów S na płaszczyznę obrazową.

Punkt główny zdjęcia O jest punktem wyznaczonym przez przecięcie łącznic łączących przeciwległe znaczki tłowe zdjęcia fotogrametrycznego. Płaszczyzna obrazowa zwana jest również płaszczyzną tłową, a układ współrzędnych - prostokątnym. Zdjęcia układem współrzędnych tłowych.

Rzut środkowy zmienia się ze zmianą położenia środka rzutów S i przedmiotów względem płaszczyzny tłowej. To właśnie położenie środka rzutów S względem płaszczyzny tłowej określają elementy orientacji wewnętrznej zdjęcia. Dla zdjęć fotogrametrycznych, gdy odległość fotografowana jest na tyle duża, że obraz powstaje w płaszczyźnie ogniskowej, odległość środka rzutów od płaszczyzny tłowej jest równa ogniskowej kamery. Położenie punktu głównego określone jest w lokalnym systemie współrzędnych zdjęcia, zwanym współrzędnych tłowych, które wyznaczają znaczki tłowe umieszczone w płaszczyźnie tłowej kamery pomiarowej. Znaczki tłowe są umieszczone zazwyczaj pośrodku na przeciwległych bokach zdjęcia i odwzorowując się na każdym zdjęciu wyznaczają w ten sposób osie układu współrzędnych tłowych.

W fotogrametrii analitycznej każde opracowanie rozpoczyna się od pomiaru na zdjęciach współrzędnych tłowych odpowiednich punktów. Pomiar ten pozwala zorientować osie tłowe zdjęcia równolegle do prostopadłych względem siebie osi układu pikselowego.

Proces obliczeniowy wymaga znajomości współrzędnych w układzie tłowym, którego początek znajduje się w punkcie głównym każdego zdjęcia. Dlatego pomiar na każdym zdjęciu wykonany na stereokomparatorze rozpoczyna się od pomiaru współrzędnych czterech znaczków tłowych.

Pomiar znaczków tłowych:

W autografie VSD AGH znaczki tłowe mierzy się następująco:

1. Manualnie - za pomocą znaczka pomiarowego ustawianego ręcznie na zdjęciach lewym i prawym, znajduje się obrazy homologiczne na obu zdjęciach.

2. Półautomatycznie - znaczek pomiarowy ustawia się ręcznie na jednym ze zdjęć bardzo dokładnie, a na drugim zdjęciu zgrubnie. Następnie włącza się pomiar półautomatyczny i program przeszukuje obszar (macierz) przeszukiwania, wyszukując obraz homologiczny o tych samych poziomach szarości, co na pierwszym zdjęciu.

Ponadto współrzędne znaczków tłowych można mierzyć całkowicie automatycznie, jednak program VSD AGH nie posiada takiej opcji.

Wcześniej do programu został wprowadzony plik ze współrzędnymi tłowymi znaczków tłowych, zaczerpnięty z metryki kalibracji kamery.

Średnie arytmetyczne współrzędnych pikselowych - po uwzględnieniu danych z kalibracji ∆x_o, ∆y_o - są współrzędnymi punktu głównego zdjęcia w układzie stereokomparatora. Współrzędne te są obarczone błędami, jakie powstają w czasie wykonania i obróbki fotograficznej zdjęć oraz ich pomiaru na stereokomparatorze. Współrzędne tłowe wykorzystywane w równaniach obserwacyjnych stosowanych do rozwiązywania zadań w fotogrametrii analitycznej nie powinny być obarczone wpływami błędów systematycznych. Błędy te spowodowane są niedoskonałością instrumentu pomiarowego oraz błędami wynikającymi z warunków wykonania zdjęć, spowodowanych niezachowaniem elementów orientacji wewnętrznej i zewnętrznej oraz refrakcją atmosferyczną i krzywizna Ziemi. Należy je wyeliminować przed rozpoczęciem dalszych obliczeń. Najbardziej niebezpiecznym źródłem błędów systematycznych jest niedociskanie materiału fotograficznego w momencie ekspozycji oraz zniekształcenia spowodowane jego obróbką i przechowywaniem.

Do wprowadzenia korekcji systematycznych błędów współrzędnych tłowych obrazu stosuje się następujące transformacje, które przekształcają pomierzone współrzędne tłowe na układ współrzędnych wzorcowych:

1. Czteroparametrową transformacje przez podobieństwo (konforemną), zwana też transformacja Hellmerta:

x = a_o + a₁x_s + b₁y_s

y = b₀ + a₁y_s - b₁x_s

Realizuje ona jednolitą zmianę skali, obrót układu współrzędnych stereokomparatora x_s, y_s, a także dwa przesunięcia.

2. Transformację bilinearną:

x = a_o + a₁x_s + a₂y_s + a₃x_sy_s

y = b₀ + b₁y_s + b₂x_s + b₂x_sy_s

3. Transformację rzutową - wykorzystywaną do pomiarów na zdjęciach niemetrycznych

x' = (A₁₁x+A₁₂y+A₁₃)/(A₃₁x+A₃₂y+1)

y' = (A₂₁x+A₂₂y+A₂₃)/(A₃₁x+A₃₂y+1)

4. Transformację afiniczną. Jest to nieco zmodyfikowana dwuwymiarowa transformacja konforemna, włączająca dla kierunków x i y różne współczynniki skalowe. Mimo, że nie zachowuje ona kształtu, linie równoległe po tej transformacji pozostają równoległe. Oprócz poprawienia skurczu za pomocą współczynników skalowych, transformacja afiniczna wprowadza również przesunięcie początku układu współrzędnych z układu współrzędnych komparatora x_s, y_s, do układu współrzędnych zdjęcia x, y oraz stosuje obrót o kąt skręcenia obydwu układów:

x = a₁ + a₂x_s + a₃y_s

y = b₁ + b₂x_s + b₃y_s

Podobnie jak w dwuwymiarowej transformacji wiernokątnej, obliczenia w transformacji afinicznej wykonuje się dwuetapowo::

1. określa się współczynniki a i b wykorzystując punkty, które znane są w obydwu układach;

2. przelicza się wszystkie punkty z układu x_s, y_s na układ x, y wykorzystując obliczone współczynniki. W celu wprowadzenia poprawek można napisać 2 równania dla każdego znaczka tłowego, czyli dla 4 znaczków tłowych 4 równania dla współrzędnej x i 4 dla współrzędnej y. Do określenia współczynników a potrzeba tylko 3 równań dla współrzędnej x, podobnie jak do wyznaczenia współczynników b wystarczą 3 równania dla współrzędnej y. Dlatego równoczesne rozwiązanie tych równań metodą najmniejszych kwadratów zwiększa dokładność wyznaczonych niewiadomych.

ORIENTACJA WZAJEMNA - Metoda Schuta

Celem jej jest określenie położenia zdjęć, takiego jakie zajmowały w momencie ich wykonania lub inaczej polega na doprowadzeniu zdjęć do takiego położenia aby patrząc przez okulary systemu obserwacyjnego autografu, widać było stereoskopowy model terenu na powierzchni całego stereogramu. Elementy orientacji wzajemnej:,   b_y, b_z, ∆ω, ∆φ, ∆χ.(jest to pomiar paralaks poprzecznych tych punktów)!!!!!!!!!!!!!!!!!!!!!!!1

Niezależna orientacja wzajemna przeprowadzana sposobem kolejnych przybliżeń wykorzystuje 6 punkt rozmieszczonych standardowo (punkty Grubera rys. 1). Punkty te nazywane są punktami orientacji - punkt 1 i 2 są rzutami punktu lewego i prawego zdjęcia, a punkty 3, 4, 5, 6 leżą w czterech narożach modelu stereoskopowego w jednakowej odległości na prostych prostopadłych do łączącej punkty 1 i 2 (bazy modelu).

Rys. 1. Rozmieszczenie punktów w strefach okołostandardowych - punkty Grubera

Dwa zdjęcia tego samego przedmiotu, wykonane z dwóch sąsiednich stanowisk, pozwalają odtworzyć przestrzenny kształt tego przedmiotu. Zespół czynności, które w analogowym przyrządzie fotogrametrycznym umożliwiają doprowadzenie, pary zdjęć do takiego względem siebie położenia, jakie zajmowały one w momencie naświetlania, nazywamy orientacją wzajemną. W takim położeniu promienie jedno-imienne, należące do dwóch wiernie zrekonstruowanych wiązek, przecinając się, tworzą model optyczny podobny do przedmiotu. Przeprowadzenie orientacji wzajem­nej jest wymagane w procesie opracowania zdjęć tylko w tym przypadku, kiedy nieznane są elementy orientacji zewnętrznej. Orientacja wzajemna jest operacją wyłącznie „wewnętrzną", nie wymaga bowiem żadnych dodatkowych informacji metrycznych o rekonstruowanym modelu.

W zależności od przyjętych warunków wyjściowych można w różny sposób zdefiniować elementy orientacji wzajemnej. Jeśli na przykład za początki układów współrzędnych x₁, y₁, z₁ oraz x₂, y₂ z₂ , przyjmie się środki rzutów dwóch sąsiednich zdjęć O₁ i O₂, przy czym założy się pionowość osi kamery zdjęcia pierwszego oraz równoległość osi układów lokalnych do osi tłowych x', y' zdjęcia pierwszego, to elementy orientacji wzajemnej można określić następująco:

∆φ — jest to różnica kątów nachylenia podłużnego, określona w płaszczyźnie x₂, z₂,

∆ω— jest to różnica kątów nachylenia poprzecznego, określona w płaszczyźnie y₂, c_k,

∆χ— jest to różnica kątów skręcenia, określona w płaszczyźnie drugiego zdjęcia

β = arc tg (bz/bx) ; jest to kąt nachylenia bazy b względem przyjętego układu odniesienia

(oś pierwszego zdjęcia pionowa, zatem płaszczyzna x₁ y₁ — pozioma),

α = arc tg (by/bx); jest to kąt zwrotu bazy b w stosunku do przyjętego układu x₁, y₁, z₁ dla pierwszego zdjęcia.

Jak widać, elementami orientacji wzajemnej jest pięć zależności pomiędzy dwiema sąsiednimi wiązkami odtworzonymi ze zdjęć. Przy czym trzy z nich są kątowe (∆φ, ∆ω, ∆χ ), a dwie liniowe, gdyż w określeniu kątów α i β tylko by i bz jest nieznana (bx nie wpływa na określenie elementów orientacji wzajemnej).

Kiedy zamiast przyjętego powyżej kryterium wyjściowego (lewe zdjęcie pionowe i układ tłowy pierwszego zdjęcia równoległy do układu lokalnego) określi się warunki początkowe inaczej, np. baza pozioma i ω'-=0, co oznacza, że oś kamery pierwszego zdjęcia leży w płaszczyźnie pionowej, to wówczas elementami orientacji wzajemnej będzie pięć następujących kątów;

φ' i φ''— kąt nachylenia podłużnego lewego i prawego zdjęcia,

χ' i χ''— kąt skręcenia lewego i prawego zdjęcia,

ω''— kąt nachylenia poprzecznego prawego zdjęcia.

Rys.2. Elementy orientacji wzajemnej.

ORIENTACJA BEZWZGLĘDNA

Pomiar fotopunktów

W zasięgu każdego stereogramu projektuje się 4 do 5 fotopunktów (punktów kontrolnych), których współrzędne X, Y, Z wyznacza się metodą geodezyjną.Są to zazwyczaj jakieś charakterystyczne punkty terenu, które można łatwo i jednoznacznie zidentyfikować na zdjęciu.. Jeżeli takich szczegółów nie ma w danym terenie, to można je zaznaczyć różnego rodzaju sygnałami (tarcze, bielone kopce, wiechy). Zadaniem fotopunktów jest zapewnienie kontroli oraz dostarczenie danych wyjściowych do korekcji w procesie kameralnego opracowania zdjęć. Między innymi używa się ich do ustalenia poprawnego modelu stereoskopowego w czasie kreślenia mapy na autografie.. Dostarczają one także danych do wyznaczenia elementów orientacji zdjęć oraz określenie poprawek do tych elementów.

Fotopunkty terenowej osnowy fotogrametrycznej są to:

1. punkty o znanych współrzędnych x, y, z

2. punkty z określonymi współrzędnymi x, y

3. punkty o znanych wysokościach z

Orientacja bezwzględna modelu doprowadza model przestrzenny do położenia właściwego w przyjętym układzie współrzędnych terenowych. Orientacja bezwzględna obejmuje czynności, które modelowi optycznemu nadają skalę oraz poziomują go, a także przyporządkowują mu prostokątny układ współrzędnych terenowych. Skalę modelu określa się przez porównanie tych samych odcinków pomierzonych na obiekcie i na modelu. Żądaną skalę można nadać modelowi przez zmianę długości bazy, to jest odległości pomiędzy środkami rzutów rozpatrywanych wiązek promieni. Poziomowanie polega na orientacji modelu w stosunku do poziomu. Osiąga się to w autografach przez obrót modelu dookoła osi X I Y instrumentu, a w opraco­waniach analitycznych przez obrót modelu wokół poziomych osi prostokątnego układu współrzędnych terenowych. Do przeprowadzenia orientacji bezwzględnej modelu potrzebna jest znajomość współrzędnych terenowych kilku punktów a mia­nowicie — co najmniej dwóch punktów sytuacyjnych oraz trzech punktów wyso­kościowych (nie leżących na jednej prostej).

Rys. 3. Orientacja bezwzględna modelu w układzie współrzędnych terenowych.

Orientację bezwzględną można przedstawić w postaci wektorowej :

X = λ*A* x + X_o

X = X_o + λ (a₁₁ x+a₁₂ y+a₁₃ z)

Y= Y_o + λ ( a₂₁ x+a₂₂ y+a₂₃ z)

Z= Z_o + λ ( a₃₁ x+a₃₂ y+a₃₃ z)

gdzie:

X - wektor terenowych współrzędnych punktów kontrolnych

λ - współczynnik zmiany skali

A - macierz obrotów, będąca funkcją kątów przestrzennego obrotu modelu

x - wektor współrzędnych modelu

X_o - wektor translacji układu modelu do układu terrenowego

Z punktu widzenia opracowania analogowego orientacja bezwzględna składa się z dwu podstawowych czynności:

- skalowania modelu terenu,

• poziomowania modelu terenu.

Skalowanie modelu stereoskopowego polega na doprowadzeniu do równości odpowiadających sobie odcinków na modelu i w terenie z uwzględnieniem skali. Zwykle wybierane są odcinki między najodleglejszymi fotopunktami terenu.

λ = dm/ D = m*√(Δx_f² + Δy_f² + Δz_f ² ) / √( Δx_g² + Δy_g² + Δz_g² )

gdzie:

d - długość przestrzennego odcinka między dwoma fotopunktami na modelu

D - długość przestrzennego odcinka między dwoma fotopunktami w terenie

1/m - skala modelu

Δx_f,Δy_f,Δz_f - przyrosty współrzędnych fotopunktów w skali modelu

Δx_g,Δy_g,Δz_g - przyrosty współrzędnych fotopunktów w terenie

Poziomowanie modelu polega na obróceniu modelu o takie kąty, aby współrzędnych przestrzennych modelu odpowiadały osiom współrzędnych w układzie terenowym- geodezyjnym. Wartości kątów obrotu kamer wynikają z porównania rzędnych Z wysokości fotopunktów w fotogrametrycznym układzie modelu i w układzie geodezyjnym. Różnice Δz = Z_ig = Z_if dla co najmniej trzech fotopunktów określają wartości kątów obrotu modelu stereoskopowego. Przy tej czynności wskazane jest takie ustawienie liczników Z-ów aby można było odczytywać bezpośrednio terenowe wysokości punktów.

Orientację bezwzględną modelu stereoskopowego nazywamy także orientacją absolutną lub geodezyjną. Zorientowany geodezyjnie model terenu jest materiałem wyjściowym do przeprowadzenia pomiarów.

Elementami orientacji bezwzględnej są:

• współczynnik skali,

• 3 przesunięcia,

• 3 obroty.

Orientacja bezwzględna:

- Rozwieranie numeryczne:

Przestrzenna transformacja przez podobieństwo :

X=Xo+ m A_L x

x - współrzędne modelu X - współrzęne obiektu

- Pomiar x dla >= 3 fotopunktów w modelu

- Wyznaczenie parametrów transformacji (7 niewiadomych) przez wyrówna­nie metodą iteracyjną

- Określenie błędów szczotkowych i dokładności

.

DTM to zbiór punktów powierzchni odpowiednio wybranych o współrzędnych X, Y, Z, utworzony jako jej numeryczna reprezentacja, oraz algorytmy umożliwiające odtworzenie jej powierzchni(kształtu) w określonym obszarze. Istnieją dwa typy DTM :

1. TIN

2. GRID

Technologia powstania DTM :

1. Technika tachimetryczna - TOTAL STATION

2. Wektoryzacja analogowych map topograficznych

- mapa analogowa na digitizerze, zdefiniowanie wysokości warstwicy, prowadzenie kursora po linii warstwicy

- skanowanie - poddanie mapy analogowej procesowi digitalizacji cyfrowej poprzez zeskanowanie i zmianę obrazu analogowego na cyfrowy; skanujemy w przedziale 256 poziomów szarości, 8 bitów, 250 - 400 dpi

Pomiar fotogrametryczny:

- w regularnej siatce kwadratów

- dynamiczna rejestracja przekrojów

- linie równych paralaks px (warstwice)

- nieregularna siatka trójkątów

- pomiar pojedynczych punktów wysokościowych w strukturze TIN lub GRID

Tryb fotogrametrycznego pomiaru DTM

- manualny

- semiautomatyczny

- automatyczny

Kompletny DTM zawiera:

- przebieg linii szkieletowych

- linie nieciągłości (granice urwisk i skarp)

- granice wyłączeń obiektów powierzchniowych - stawy, jeziora

- granice wyłączeń obszarów o jednolitym spadku, np. rzek o szerokości > 5m.

- lokalne ekstrema wysokościowe

Dokładność DTM wyrażają parametry metrycznej dokładności natomiast jakość DTM wyrażają kompletność i adekwatność opisu form geomorfologicznych terenu.

Wynikowa dokładność DTM:

m_DTM = 0,20 - 0,40 ‰W - teren łatwy

m_DTM = 1,00 - 2,00 ‰W - teren trudny

Dokładność wynikowa DTM zależy od:

- błędów danych źródłowych

- wielkości oczka siatki

- charakteru rzeźby terenu

- metody interpolacji

Wynikowy DTM jest w strukturze GRID

Cechy struktury TIN :

- zachowuje związki topologiczne między punktami pomiarowymi

- opisuje i zachowuje w jednakowej strukturze opis morfologicznych form terenowych

- archiwizacja DTM w TIN wymaga większych zbiorów, brak algorytmów automatycznego generowania

Cechy struktury GRID:

- regularna sieć kwadratów lub prostokątów

- powstaje przez interpolację struktury TIN

- większa łatwość modelowania powierzchni

- interpolacja może nastąpić w dowolnym punkcie

- możliwość dowolnego generowania profili

- łatwość obliczeń objętości

- łatwa wizualizacja 3D

- określenie widoczności między punktami

- łatwość tworzenia spadków i ekspozycji

- DTM w strukturze GRID jest najbardziej przydatny do wygenerowania ortofotomapy

- łatwość archiwizacji(siatka punktów tworzy tzw. macierz wysokości)

Interpolacja DTM:

1. Tryb pomiarów manualnych w trybie pomiarów stereofotogrametrycznych

2. Tryb pomiarów semiautomatycznych

3. Tryb pomiarów automatycznych

Metodę automatycznego generowania DTM wykonujemy gdy:

- wykonujemy DTM dla terenów odkrytych ze zdjęć średnio i małoskalowych

- w innych przypadkach warunkowe generowanie automatyczne wspomagane pomiarem manualnym

Zaleca się w pierwszej kolejności generowanie automatyczne a pomiar manualny w ramach uzupełnienia. Możliwość zastosowania operatorów automatycznego generowania DTM wynika z czterech warunków:

1. Musi być wyraźna tekstura powierzchni obiektu

2. Tereny nie mogą być zalesione i zabudowane

3. Różnica orientacji nie może przekraczać 30^o

4. Różnice skal zdjęcia lewego i prawego nie mogą przekraczać 25%

Dla pomiaru z automatycznym generowaniem stosujemy metodę matching`u

Kontrola jakości DTM polega na:

- porównaniu przebiegu warstwic wygenerowanych z DTM z warstwicami na analogowej mapie topograficznej

- porównaniu wygenerowanych warstwic z wizualną oceną modelu stereoskopowego terenu

- porównaniu wysokości wyinterpolowanych rzędnych z wysokościami określonymi metodami niwelacji technicznej lub trygonometrycznej

Podczas zajęć dydaktycznych wykonano DTM w trybie pomiarów manualnych , oparty na siatce kwadratów o oczku 25 m

POMIAR WSPÓŁRZĘDNYCH PIKSELOWYCH

Wykonanie ćwiczenia:

Dane wyjściowe: zdjęcia Olsztyna wykonane w ramach programu Phare 1995 kamera UMK o C_k = 305,21 mm. Były skanowane na skanerze Photoscan PS1 Zeiss. Jest to typowy skaner fotogrametryczny, dokładność- 7,5 μ 8 3 = 22,5 μm, skanowanie w trzech kanałach RGB 24 bit, ( 3 * 256 ) zapisane w formacie pliku *.tif, co daje w przybliżeniu 310 MB pojemności dla każdego obrazu.

Dokonano preprocessing ( wstępnego przetwarzania, który polega na tym, że z RGB uzyskujemy obraz czarno biały- 8 bit głębia zapisu, 1 * 256 poziom szarości, format zapisu *.tif co daje 102 MB pojemności dla każdego obrazu.

Dokonano automatycznie wyrównania poziomów, poprawiono współrzędne kontrastowe γ = 1,5.

Utworzono katalog roboczy oraz katalog ze zdjęciami i z wynikami.

Katalog roboczy: D:\ GiSN_04\gr.2\model 1

Katalog obrazowy: D:\Olsztyn\317.tif

Pomiar znaczków tłowych

• manualny- z wypozycjonowaniem lewego i prawego kursora na znakach tłowych

• półautomatyczny- obraz pozycjonowany znaleziony jest przez dopasowanie korelacji

• automatyczny- samodzielne wyznaczenie na zdjęciu

Wykonując pomiar znaczków tłowych nie można do końca zawierzyć autokorelacji.

Przechodząc z układu pikselowego na układ tłowy dokonujemy transformacji:

- konforemna

- pseudoafiniczna

- afiniczna

1. transformacja przez podobieństwo (konforemna) transformacja Helmerta - zachowuje kąty w skali. Mamy do wyznaczenia 4 wsp, które opisują nam model korekcji tak, że musimy mieć 2 znaczki tłowe z pomierzonymi wsp tłowymi z uwzględnieniem kalibracji kamery. Możemy wtedy ułożyć 4 równania obserwacyjne rozwiązać je metodą podstawienia i wyznaczyć niewiadome: a₀, b₀, a, b. Zakładamy tu, że: osie układu są ortogonalne, zniekształcenia skali wzdłuż obu osi są jednakowe (2 pkt dostosowania)

x' = a₀ + a₁x_s' - b1y_s'

y' = b₀ + b₁x_s' - a1y_s'

gdzie: x_s', y_s' - w układzie stereokomparatora

2. pseudoafiniczna (bilinearna) - musimy wyznaczyć współczynnik, stąd potrzeba 4 znaczków tłowych. Stosowanie metod ścisłych jest utrudniona, ponieważ brak tu obs nadliczbowych, tzn układ równań jest słabo określony. Transformacja ta nie powinna być stosowana w przypadku kamer z 4 znaczkami tłowymi.

x' = a₀ +a₁x_s' + a₂y_s' + a₃x_s'y_s'

y' = b₀ + b₁x_s' + b₂y_s' + b₃x_s'y_s'

3. transformacja afiniczna jest to nieco zmodyfikowana dwuwymiarowa transformacja konforemna, włączająca dla kierunków x i y różne współczynniki skalowe. Mimo że nie zachowuje ona kształtu, linie równoległe po tej transformacji pozostają równoległe. Oprócz poprawienia skurczu za pomocą współczynników skalowych, transformacja afiniczną wprowadza również przesunięcie początku układu współrzędnych z układu współrzędnych komparatora x,, y, do układu współrzędnych zdjęcia x, y oraz stosuje obrót o kąt skręcenia obydwu układów:

x=a₁+a₂x_s+a₃y_s

y=b₁+b₂x_s+b₃y_s

Podobnie jak w dwuwymiarowej transformacji wiernokątnej, obliczenia w trans­formacji afinicznej wykonuje się dwuetapowo:

1) określa się współczynniki a i b wykorzystując punkty, które znane są w oby­dwu układach;

2) przelicza się wszystkie punkty z układu x_s, y_s, na układ x y, wykorzystując obliczone współczynniki. W celu wprowadzenia poprawek można napisać dwa równania dla każdego znaczka tłowego, czyli dla czterech znaczków tłowych cztery równania dla współrzędnej x i cztery dla współrzędnej y. Do określe­nia współczynników a potrzeba tylko trzech równań dla współrzędnej x, podobnie jak do wyznaczenia współczynników b wystarczą trzy równania dla współrzędnej y. Dlatego równoczesne rozwiązanie tych równań metodą najmniejszych kwadratów zwiększa dokładność wyznaczonych niewiadomych.

Etapy:

I - określenie wsp a i b wykorzystując pkt, które znane są w obydwu układach

II - przeliczenie wszystkich pkt z układu xs, ys na układ x, y wykorzystując obliczone współczynniki. W celu wprowadzenia poprawek można napisać 2 równania typu (wyżej) dla każdego znaczka tłowego, czyli dla 4 znaczków tłowych 4 równania Mz współrzędnych x i 4 dla y. Dla określenia współczynnika a potrzeba tylko 3 równań dla wsp x, podobnie jak dla współczynnika b wystarczają 3 równania Mz wsp y. Dlatego równoczesne rozwiązanie tych równań met najmniejszych kwadratów zwiększa dokładność wyznaczanych niewiadomych.

BUDOWA POJEDYNCZEGO MODELU METODĄ ETAPOWA Z WYKORZYSTANIEM SYSTEMU VSD.

1.Orientacja wewnętrzna (transformacja do układu tłowego):

- pomiar 4 lub więcej znaczków tłowych (min. 2 znaczki) i rejestracja klawiszem [I]. Aby wykorzystać do obliczeń transformacji współrzędne tłowe znaczków zapisane w pliku NazwaZadania.PKT należy po wprowadzeniu numeru punktu nacisnąć klawisz [INSERT].

- obliczenie współczynników jednej z czterech transformacji do wyboru - klawisz [F5] (obliczenia mogą być wykonane bezpośrednio po zarejestrowaniu punktów lub po zakończeniu pomiarów dla orientacji wzajemnej i bezwzględnej)

Elementy orientacji wewnętrznej pozwalają na odtworzenie wiązki promieni rzucających. Są to elementy liniowe określające położenie środka rzutów S w stosunku do płaszczyzny obrazowej ( ). Elementami orientacji wewnętrznej zdjęcia są :

1. odległość obrazowa kamery fotogrametrycznej Ck ( f= Ck )

2. współrzędne punktu głównego zdjęcia o (x₀, y₀ ) stanowiącego rzut prostokątny środka rzutów S na płaszczyznę obrazową

3. dystorsja radialna i tangencjalna

Punkt główny zdjęcia O jest punktem wyznaczonym przez przecięcie łącznic łączących przeciwległe znaczki tłowe zdjęcia fotogrametrycznego.

Rzut środkowy zmienia się ze zmianą położenia środka rzutów S i przedmiotów względem płaszczyzny tłowej. To właśnie położenie środka rzutów S względem płaszczyzny tłowej określają elementy orientacji wewnętrznej zdjęcia.

Dla zdjęć fotogrametrycznych gdy odległość fotografowana jest na tyle duża , że obraz powstaje w płaszczyźnie ogniskowej , odległość środka rzutów od płaszczyzny tłowej jest równa ogniskowej kamery.

Położenie punktu głównego określone jest w lokalnym systemie współrzędnych zdjęcia , zwanym współrzędnych tłowych, które wyznaczają znaczki tłowe umieszczone w płaszczyźnie tłowej kamery pomiarowej. Znaczki tłowe są umieszczone zazwyczaj pośrodku na przeciwległych bokach zdjęcia i odwzorowując się na każdym zdjęciu wyznaczają w ten sposób osie układu współrzędnych tłowych.

2. Orientacja wzajemna (obliczenie współrzędnych przestrzennych w układzie modelu):

- pomiar 6 lub więcej punktów homologicznych (min. 5 punktów) i zarejestrowanie ich [H] (pomiar punktu może być wykonany półautomatyczną metodą autokorelacji [F9] - aktualnie funkcja jest dostępna dla obrazów monochromatycznych)

- obliczenie elementów orientacji wzajemnej oraz współrzędnych przecięcia promieni homologicznych w układzie modelu [F6] (z wprowadzeniem z klawiatury elementów orientacji wewnętrznej ck, xo i yo oraz ew. wartości współczynników dystorsji radialnej z pliku NazwaZadania.ADP) ,

- Po wykonaniu orientacji wzajemnej istnieje możliwość uruchomienia trybu autogrametrycznego w układzie modelu (warunek: pomierzonych min 6 punktów).

Elementy orientacji wzajemnej:

-Δϕ -różnica między kątami nachylenia podłużnego

-Δω -różnica między kątami nachylenia poprzecznego

-Δκ-różnica między kątami skręcenia

-kąt nachylenia bazy względem przyjętego układu odniesienia

-kąt zwrotu bazy w stosunku do przyjętego układu x₁,y₁,z₁, dla pierwszego

zdjęcia

METODA SCHUTA

Metodę tę stosuje się, gdy układ zdefiniowany jest tu umownie (BxF')*F''=0 pozornym lewym zdjęciem. Początkowo punkty przestrzeni przedmiotowej powinny znajdować się w płaszczyznach rdzennych (komplementarności). Na początku zakładamy dla lewego zdjęcia, że φ', ω', χ' = 0, poprawki dla współrzędnych tłowych x', x'' = 0, natomiast poprawki dla y', y'' różnią się znakami, a więc redukują się. Niewiadomymi w równaniu są: b_y, b_z i współrzędne x'', y'', z'' będące współrzędnymi promienia rzutującego r'' określonymi pomierzonymi na zdjęciu wspólrzędnymi x'', y'', C_K, φ'', ω'', χ''. Dlatego poszukiwanymi niewiadomymi są: b_y, b_z, φ'', ω'', χ''.

Etapy orientacji:

1. rozwiązanie danego układu równań normalnych przy założeniu, że bx = 1,
   ;

2. tworzymy i rozwiązujemy układ równań poprawek paralaksy porzecznej dφ, dω, dχ;

3. utworzenie nowej macierzy obrotu R⁽²⁾ _;

4. trzeba wykorzystać macierz obrotu i przemnożyć
   gdzie: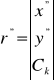
   ;

5. 
   - wyznaczenie elementów orientacji wzajemnej ;

6. tworzymy macierz obrotu R⁽³⁾;

Ten cykl jest realizowany dopóki otrzymamy minimalne poprawki. Ostateczne wyznaczone elementy orientacji wzajemnej są sumą przyrostów z kolejnych iteracji.

3.Orientacja bezwzględna (transformacja przestrzenna z układu modelu do układu odniesienia ):

-pomiar 3 lub więcej punktów dostosowania (x,y,z) i rejestracja klawiszem [G]

W celu użycia współrzędnych geodezyjnych zapisanych w pliku Nazwa Zadania. PKT należy po wprowadzeniu numeru punktu nacisnąć klawisz [INSERT].

- obliczenie elementów orientacji bezwzględnej klawiszem [F7].

Na orientację bezwzględną składa się:

-skalowanie modelu

-poziomowanie modelu

Do przeprowadzenia orientacji bezwzględnej modelu jest potrzebna znajomość współrzędnych terenowych kilku punktów (co najmniej dwóch punktów sytuacyjnych oraz trzech punktów wysokościowych nie leżących na jednej prostej). Polega ona na przetransformowaniu układu lokalnego (układu współrzędnych modelu) do układu współrzędnych terenowych. Początkiem lokalnego układu współrzędnych jest środek rzutów lewego zdjęcia a oś celowa lewego zdjęcia pokrywa się z osią układu współrzędnych. Zależność między tymi dwoma układami opisana jest wektorami. Wektor x₀ opisuje odległość wektorową między układem współrzędnych geodezyjnych a środkiem rzutów układu współrzędnych modelu; wektor x_S opisuje położenie punktu w układzie współrzędnych geodezyjnych, a wektor x - w układzie modelu.

Sposób zapisu wcięcia w przód: x_S=x₀+mR_x

Otrzymujemy tu zespół równań z 7 parametrami transformacji x₀, y₀, z₀ (składowe przesunięcia wektora translacji) elementy kątowe φ, ω, χ macierzy obrotu oraz współrzędne zmiany skali m. Może być tak, że współczynnik zmiany skali wzdłuż każdej osi jest inny (m_x, m_y, m_z) i wtedy mamy 9 niewiadomych. Aby obliczyć 7 parametrów w sposób ścisły trzeba mieć min 7 obserwacji. Najczęściej stosuje się 3 pełne fotopunkty, z czego można ułożyć 9 równań. Układ poprawek rozwiązujemy metodą najmniejszych kwadratów i w konsekwencji otrzymujemy parametry transformacji przestrzennej. Parametry te otrzymujemy w procesie iteracyjnym. Teraz korzystając z tych równań obliczamy x, y, z, każdego punktu, który nie jest w danym modelu fotopunktem.

Elementy orientacji wewnętrznej zdjęcia

Parametry orientacji:

• Stała kamery C_k

• Współrzędne punktu głównego: ∆x_o^', ∆y_o^'

• Dystorsje: radialna dr_r^', tangencjalna dr_tg^'

Elementy orientacji zewnętrznej zdjęcia (można obliczyć z warunku kolinearności lub z wykorzystaniem przekształceń rzutowych)

Parametry orientacji:

• Współrzędne środka rzutów w układzie terenowym x_o, y_o, z_o.

• Kąt nachylenia poprzecznego ω wokół osi X

• Kąt nachylenia podłużnego φ wokół osi Y

• Skręcenie zdjęcia κ

---