WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM GRAFIKI KOMPUTEROWEJ

SPRAWOZDANIE

Temat: Modelowanie obiektów 3D

Data realizacji ćwiczenia: 06.04.2005

Prowadzący: dr inż. Marek Salamon

Wykonawca: Anna Pokrzywa

grupa C02A

I Zadanie laboratoryjne:

Wykorzystując wybrane funkcje modelowania geometrycznego biblioteki OpenGL/Glut napisać program przedstawiający perspektywiczny obraz bryły 3D o poniższych parametrach:

- stożek w trybie GL_TRIANGLE_STRIP o promieniu dolnej podstawy 2 i jej środku w punkcie (0,0,0), oraz promieniu górnej podstawy 1 i wysokości 1.

- podstawy figury zamodelować w trybie GL_TRIANGLE_FUN

-przewidzieć możliwość zmiany liczby podziałów pionowych i poziomych

II Sposób rozwiązania zadania :

Do realizacji swojego ćwiczenia laboratoryjnego wykorzystałam, udostępnione w trakcie zajęć, programy rysujące walec i sześcian w trój-wymiarze.

Zaimplementowany przeze mnie algorytm wykorzystywał następujące zmienne :

• h - wysokość modelowanego stożka

• r - promień dolnej podstawy stożka

• r2 - promień górnej podstawy stożka

• nv - zmienna określająca ilość podziałów poziomych

• nh - zmienna określająca ilość podziałów pionowych

• dH ­- wysokość pojedynczego wycinka poziomego

• dAlfa - wartość kąta wyznaczającego pojedynczy wycinek pionowy

• dR - różnica promieni dwóch sąsiadujących wycinków poziomych

Poszczególne wartości zmiennych wyznaczyłam z następujących zależności:

• h,r,r2,nv,nh - zadane na wejściu

• dH = h/nv - wysokość jednego wycinka poziomego wynika z podzielenia całkowitej wysokości stożka przez liczbę wszystkich wycinków poziomych

• dAlfa =360.0L/nh - kąt pojedynczego wycinka pionowego wynika z podzielnia 360 stopni przez liczbę wszystkich wycinków pionowych

• dR=(r-r2)/nv - różnica promieni dolnej i górnej podstawy stożka, podzielona przez liczbę podziałów poziomych daje wartość o jaką różnią się promienie dwóch sąsiadujących podziałów

Pętla odpowiedzialna za narysowanie dolnej podstawy stożka:

(1) glBegin(GL_TRIANGLE_FAN) ;

(2) glVertex3f(0.0 , 0.0 , 0.0) ;

(3) for(i=0 ; i*dAlfa <= 360.0L ; i++)

{

(4) glVertex3f(r*cos(DEG2RAD(i*dAlfa)) , 0.0 , r*sin(DEG2RAD(i*dAlfa)));

}

(5) glEnd();

W pierwszej linii kodu zostaje zadeklarowana metoda, którą wykorzystałam do narysowania dolnej podstawy stożka (1). Deklaracja taka posiada poniższy schemat:

glBegin(nazwa_prymitywa) ; - rozpoczęcie bloku tworzenia prymitywa

Przyjętym przeze mnie prymitywem była metoda GL_TRIANGLE_FAN. Polega ona na łączeniu trzech punktów:

-pierwszego zadeklarowanego

- ostatniego zadeklarowanego

- aktualnie deklarowanego

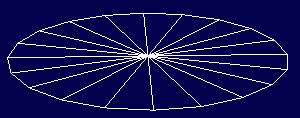
w trójkąt. W następnej linii kodu (2), w punkcie o współrzędnych (0,0,0), deklaruje położenie środka dolnej podstawy stożka. W tym celu wykorzystuję funkcję `glVertex3f', tworzącą wierzchołek trójwymiarowy, o współrzędnych typu Glfloat (x,y,z). Kolejno wykonywana jest pętla (3), w której definiowane są punkty, leżące na okręgu podstawy. Współrzędne tych punktów zmieniają się zależnie od wartości zmiennej `i', określającej aktualnie rysowany wycinek pionowy. Ponad to do wyznaczenia powyższych współrzędnych wykorzystuję zależności wynikające z funkcji trygonometrycznych kątów. Przy czym należy pamiętać o zamianie wartości kątów ze stopni na radiany, a także o fakcie iż tylko dwie współrzędne ulegają zmianie. Wysokość pozostaje stała i wynosi zero. Punkty definiowane w pętli (4) są łączone ze środkiem podstawy - punktem (0,0,0). Otrzymany obraz wygląda następująco:

Rys.1

Poleceniem glEnd( ); (5) kończony jest blok tworzenia prymitywa.

Pętla odpowiedzialna za narysowanie górnej podstawy stożka:

glBegin(GL_TRIANGLE_FAN) ;

glVertex3f(0.0 , h , 0.0) ;

for(i=0 ; i*dAlfa <= 360.0L ; i++)

{

glVertex3f(r2*cos(DEG2RAD(i*dAlfa)) , h , r2*sin(DEG2RAD(i*dAlfa)));

}

glEnd();

Algorytm ten jest analogiczny do algorytmu rysującego dolną podstawę opisanego powyżej . Jedyne różnice dotyczą położenia i wielkości podstawy. Jest ona rysowana na wysokości `h' i ma promień równy `r2'.

Wyznaczenie ścian bocznych stożka:

(1) for(i=0 ; floor((i+1)*dH*1.0E10) <= floor(h*1.0E10) ; i++)

{

2. glBegin(GL_TRIANGLE_STRIP) ;

3. for(j=0 ; j*dAlfa <= 360.0L ; j++)

{

(4) glVertex3f(r*cos(DEG2RAD)j*dAlfa)) , i*dH , r*sin(DEG2RAD(j*dAlfa)));

(5) glVertex3f((r-dR) * cos(DEG2RAD(j*dAlfa)) , (i+1)*dH , (r-dR) *

sin(DEG2RAD(j*dAlfa)));

}

(6) glEnd() ;

(7) r=r-dR ;

}

Algorytm rozpoczyna się od pętli (1) określającej, który wycinek poziomy jest aktualnie rysowany. Na każdy taki wycinek składa się `nh' podziałów pionowych. W dalszej części algorytmu określona została metoda wykorzystana do narysowania powierzchni bocznej stożka (2) - GL_TRIANGLE_STRIP. Polega ona na łączeniu ze sobą trzech ostatnio narysowanych punktów. Nowy punkt jest łączony z dwoma poprzednimi trwożąc trójkąt.

Następna, zagnieżdżona pętla (3) odpowiada za rysowanie wycinków pionowych. Wykorzystuje ona funkcję `glVertex3f' (4) i (5), tworzącą wierzchołek trójwymiarowy, o współrzędnych typu Glfloat (x,y,z). Pierwszy punkt w tej pętli zostaje zdefiniowany na wysokości h=0 i leży na obwodzie podstawy dolnej stożka. Drugi punkt jest rysowany na wysokości `dH'. Ponadto do jego wyznaczenia używam promienia `r' pomniejszonego o `dR'. Punkty są ze sobą łączone. Warunek pętli zostaje zwiększony o kąt `dAlfa' (3) i rozpoczyna się tworzenie kolejnego wycinka pionowego. Gdy warunek pętli zagnieżdżonej zostaje niespełniony - sumy kątów `dAlfa' dały wartość większą lub równą 360 stopni - oznacza to że skończone zostało rysowanie wycinka poziomego wraz ze wszystkimi składającymi się na niego wycinkami pionowymi. Obrazuje to poniższy rysunek:

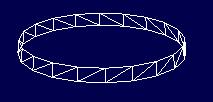
Rys. 2

Tworzenie nowego wycinka poziomego zaczyna się przez dodanie wartości `dH' (1) do wysokości ostatnio tworzonego fragmentu (pętla zewnętrzna). Ponadto wartość promienia `r' pomniejszona zostaje o `dR' (7). Rozpoczyna się modelowanie kolejnego poziomego fragmentu. Pętle zewnętrzne (1) są wywoływane do momentu aż kolejne sumy `dH' będą równe wysokości `h'. Jednocześnie, ciągle pomniejszany, promień r osiągnie wartość wynoszącą `r2'. Końcowym efektem opisywanego algorytmu jest następujący obraz:

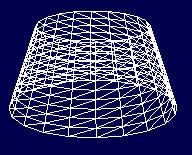
Rys. 3

Polecenie glEnd( ); (6) kończy blok tworzenia prymitywa.

Pełen algorytm rysujący stożek o promieniu dolnej podstawy 2 i jej środku w punkcie (0,0,0), oraz promieniu górnej podstawy 1 i wysokości 1 w trybie GL_TRIANGLE_STRIP:

void RysujStozek(double h, double r, int nv, int nh)

{

int i, j;

double dH, dAlfa,r2,dR;

r2 = 1.0;

dR=(r-r2)/nv;

dAlfa = 360.0L/(double)nh; - wyznaczenie kata określającego pojedynczy wycinek

pionowy

dH = h/(double)nv; - wyznaczenie wysokości pojedynczego wycinka poziomego

glBegin(GL_TRIANGLE_FAN); - początek podstawy dolnej

glVertex3f(0.0, 0.0, 0.0);

for (i = 0; i * dAlfa <= 360.0L; i++)

{

glVertex3f(r*cos(DEG2RAD(i*dAlfa)),0.0,r*sin(DEG2RAD(i*dAlfa)));

}

glEnd(); - koniec podstawy dolnej

glBegin(GL_TRIANGLE_FAN); - początek podstawy górnej

glVertex3f(0.0, h,0.0);

for (i = 0; i * dAlfa <= 360.0L; i++)

{

glVertex3f(r2*cos(DEG2RAD(i*dAlfa)),h,r2*sin(DEG2RAD(i*dAlfa)));

}

glEnd(); - koniec podstawy górnej

for (i = 0; floor((i+1)*dH*1.0E10) <= floor(h*1.0E10); i++) - początek wyznaczania

{ ścian bocznych

glBegin(GL_TRIANGLE_STRIP);

for(j = 0; j * dAlfa <= 360.0L; j++)

{ glVertex3f(r*cos(DEG2RAD(j*dAlfa)),i*dH,r*sin(DEG2RAD(j*dAlfa)));

glVertex3f((r-dR)*cos(DEG2RAD(j*dAlfa)),(i+1)*dH,((r-dR)*sin(DEG2RAD

(j*dAlfa))));

}

glEnd();

r=r-dR;

} - koniec wyznaczania ścian bocznych

}

Wynik powyższego algorytmu:

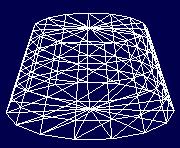
Rys. 4

III Wyniki

Celem ćwiczenia laboratoryjnego było zamodelowanie w przestrzeni trójwymiarowej stożka.

Do wyznaczenia ścian bocznych należało wykorzystać metodę GL_TRIANGLE_STRIP, natomiast do narysowania podstaw metodę GL_TRIANGLE_FAN. Ponadto należało przewidzieć możliwość zmiany liczby podziałów poziomych i pionowych.

Korzystając z liczby podziałów pionowych, uwzględniając zadaną metodę modelowania, wyznaczyłam fragmenty składające się na jeden wycinek poziomy ścian bocznych stożka (rys. 2). Podziały poziome posłużyły mi do rysowania kolejnych odcinków wysokości tworzących ściany boczne. Kolejno rysowane punkty ścian bocznych wyznaczałam w następującej kolejności:

• wyznaczenia dwóch pierwszych punktów dla ściany

• wyznaczanie pary punktów ściany przy użyciu funkcji opisującej ruch po okręgu, z wykorzystaniem zależności trygonometrycznych kątów :

glVertex3f(r*cos (DEG2RAD(j*dAlfa)), i*dH, r*sin (DEG2RAD(j*dAlfa)))

gdzie:

r - promień walca

i,j - zmienne pętli

dH - wysokość podziału poziomego

dAlfa - kąt podziału pionowego

Efektem tych działań jest rys. 3.

Podstawę górną i dolną wyznaczyłam w oparciu o podział pionowy, również z wykorzystaniem metody ” glVertex3f(); ” (rys. 1).

Efekt końcowy działania programu przedstawia rys. 5. Jest on wynikiem połączenia zamodelowanych podstaw i ścian bocznych stożka. Figura powstała z połączenia kolejno deklarowanych trójkątów.

Modyfikacja bryły jest możliwa poprzez zmianę wartości parametrów wysokości i promieni, oraz zwiększenie lub zmniejszenie liczby podziałów pionowych i poziomych w celu modyfikacji dokładności utworzonego obrazu. Wszelkich zmian parametrów stożka można dokonać jedynie w kodzie programu.

IV Pełen wydruk programu

Na wydruku czerwonym kolorem zaznaczyłam miejsce modyfikacji parametrów stożka. Kolorem bordowym zaznaczony jest napisany przeze mnie algorytm oraz definicje i deklaracje niezbędne do wywołania tego algorytmu.

//////////////////////////////////////////////////////////////////////////////////////////

// Program przedstawiajacy stożek w rzucie perspektywicznym

//////////////////////////////////////////////////////////////////////////////////////////

// Definicja bibliotek

#include <math.h>

#include <string.h>

#include <stdio.h>

#include <GL/glut.h>

// Definicja stalych

#define OBSERWATOR_ODLEGLOSC 20.0

#define OBSERWATOR_OBROT_X 20.0

#define OBSERWATOR_OBROT_Y 20.0

#define OBSERWATOR_FOV_Y 30.0

#define M_PI 3.1415

#define DEG2RAD(x) ((float)(x)*M_PI/180.0)

// Zmienne globalne

int szerokoscOkna = 800;

int wysokoscOkna = 600;

int podzialpionowy = 20;

int podzialpoziomy = 20;

double wysokosc = 1.0;

double promien = 1.0;

// Prototypy funkcji

void RysujStozek(double h,double r,int nv, int nh);

void UstawParametryWidoku(int szer, int wys);

void WyswietlObraz(void);

void ObslugaKlawiatury(unsigned char klawisz, int x, int y);

//////////////////////////////////////////////////////////////////////////////////////////

// Funkcja rysujaca stożek o promieniu dolnej podstawy

//2 i jej środku w punkcie (0,0,0) oraz promieniu gornej podstawy 1

// i wysokosci 1 w trybie GL_TRIANGLE_STRIP

void RysujStozek(double h, double r, int nv, int nh)

{

int i, j;

double dH, dAlfa,r2,dR,dR2;

r2 = 1.0;

dR=(r-r2)/nv;

// Wyznaczenie kata wyznaczajacego pojedynczy wycinek pionowy

dAlfa = 360.0L/(double)nh;

// Wyznaczenie wysokosci pojedynczego wycinka poziomego

dH = h/(double)nv;

// Podstawa dolna

glBegin(GL_TRIANGLE_FAN);

glVertex3f(0.0, 0.0, 0.0);

for (i = 0; i * dAlfa <= 360.0L; i++)

glVertex3f(r*cos(DEG2RAD(i*dAlfa)),0.0,r*sin(DEG2RAD(i*dAlfa)));

glEnd();

/* //podstawa gorna

glBegin(GL_TRIANGLE_FAN);

glVertex3f(0.0, h,0.0);

for (i = 0; i * dAlfa <= 360.0L; i++)

glVertex3f(r2*cos(DEG2RAD(i*dAlfa)),h,r2*sin(DEG2RAD(i*dAlfa)));

glEnd();

*/

// Wyznaczanie scian pocznych

for (i = 0; floor((i+1)*dH*1.0E10) <= floor(h*1.0E10); i++)

{

glBegin(GL_TRIANGLE_STRIP);

for(j = 0; j * dAlfa <= 360.0L; j++)

{

glVertex3f(r*cos(DEG2RAD(j*dAlfa)),i*dH,r*sin(DEG2RAD(j*dAlfa)));

glVertex3f((r-dR)*cos(DEG2RAD(j*dAlfa)),(i+1)*dH,((r-dR)*sin(DEG2RAD(j*dAlfa))));

}

glEnd();

r=r-dR;

}

}

//////////////////////////////////////////////////////////////////////////////////////////

// Funkcja ustawiajaca parametry rzutu perspektywicznego i rozmiary viewportu

void UstawParametryWidoku(int szer, int wys)

{

// Zapamietanie wielkosci widoku

szerokoscOkna = szer;

wysokoscOkna = wys;

// Ustawienie parametrow viewportu

glViewport(0, 0, szerokoscOkna, wysokoscOkna);

// Przejscie w tryb modyfikacji macierzy rzutowania

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

gluPerspective(OBSERWATOR_FOV_Y, (float)szerokoscOkna/(float)wysokoscOkna, 1.0, 1000.0);

// Przejscie w tryb modyfikacji macierzy przeksztalcen geometrycznych

glMatrixMode(GL_MODELVIEW);

// Zmiana macierzy znajdujacej sie na wierzcholku stosu na macierz jednostkowa

glLoadIdentity();

// Wyswietlanie wielokatow w postaci obrysow.

glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);

}

//////////////////////////////////////////////////////////////////////////////////////////

// Funkcja generujaca pojedyncza klatke animacji

void WyswietlObraz(void)

{

// Wyczyszczenie bufora ramki i bufora glebokosci

glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);

// Okreslenie wielkosci widoku, wlaczenie rzutowania perspektywicznego

// i zainicjowanie stosu macierzy modelowania

UstawParametryWidoku(szerokoscOkna, wysokoscOkna);

// Ustalenie polozenia obserwatora

glTranslatef(0, 0, -OBSERWATOR_ODLEGLOSC);

glRotatef(OBSERWATOR_OBROT_X, 1, 0, 0);

glRotatef(OBSERWATOR_OBROT_Y, 0, 1, 0);

// Generacja obrazu stozka

RysujStozek(wysokosc,promien,podzialpoziomy,podzialpionowy);

// Przelaczenie buforow ramki

glutSwapBuffers();

}

//////////////////////////////////////////////////////////////////////////////////////////

// Glowna funkcja programu

int main(int argc, char **argv)

{

// Zainicjowanie biblioteki GLUT

glutInit(&argc, argv);

// Ustawienie trybu wyswietlania

glutInitDisplayMode (GLUT_DOUBLE|GLUT_RGBA|GLUT_DEPTH);

// Ustawienie polozenia dolenego lewego rogu okna

glutInitWindowPosition(100, 100);

// Ustawienie rozmiarow okna

glutInitWindowSize(szerokoscOkna, wysokoscOkna);

// Utworzenie okna

glutCreateWindow("Stozek");

// Odblokowanie bufora glebokosci

glEnable(GL_DEPTH_TEST);

// Ustawienie funkcji wykonywanej na danych w buforze glebokosci

glDepthFunc(GL_LEQUAL);

// Ustawienie wartosci czyszczacej zawartosc bufora glebokosci

glClearDepth(1000.0);

// Ustawienie koloru czyszczenia bufora ramki

glClearColor (0.0f, 0.0f, 0.3f, 0.0f);

// Zarejestrowanie funkcji (callback) wyswietlajacej

glutDisplayFunc(WyswietlObraz);

// Zarejestrowanie funkcji (callback) wywolywanej za kazdym razem kiedy

// zmieniane sa rozmiary okna

glutReshapeFunc(UstawParametryWidoku);

// Zarejestrowanie funkcji wykonywanej gdy okno nie obsluguje

// zadnych zadan

glutIdleFunc(WyswietlObraz);

// Obsluga glownej petli programu (wywolywanie zarejestrowanych callbackow

// w odpowiedzi na odbierane zdarzenia lub obsluga stanu bezczynnosci)

glutMainLoop();

return 0;

}

7

---