1. Dla pkt materialnego: def. momentu pędu i siły,
II zasadę dynamiki dla ruchu obrotowego,

prawo zachowania momentu pędu:

Momentem siły względem danego punktu (lub osi) nazywany iloczyn wektorowy wektora wodzącego przez wektor siły. M = r x F

Moment siły jest wektorem prostopadłym do płaszczyzny wyznaczonej przez wektor siły i wektor wodzący o zwrocie zgodnym z kierunkiem ruchu śruby prawoskrętnej obracanej od r do F o wartości: M = r F sinα,

gdzie α - kąt jaki wektor r i F tworzą ze sobą

Momentem pędu (kręt) ciała względem osi obrotu nazywamy wektor o wielkości równej iloczynowi momentu bezwładności przez wielkość prędkości kątowej względem tej osi, o zwrocie i kierunku zgodnym ze zwrotem i kierunkiem wektora prędkości kątowej. L = J ω

II zasada dynamiki dla ruchu obrotowego - jeżeli na ciało sztywne działa niezrównoważony moment siły, to moment ten nadaje ciału przyspieszenie kątowe, którego wartość jest wprost proporcjonalna do wartości momentu siły i odwrotnie proporcjonalna do momentu bezwładności ciała. ε=M/J; Prawo zachowania momentu pędu - dla dowolnego izolowanego układu punktów materialnych całkowita suma momentów pędu każdego pkt mat jest stała: ΔL/Δt=M

2. Podać wyrażenie na moment bezwł. bryły względem ustalonej osi, TW Steinera i dowód tego twierdzenia

Moment bezwładności - sumia iloczynów mas poszcz. elementów bryły i kwadratów ich odległości od osi obrotu.

Twierdzenie Steinera Moment bezwł. dowolnego ciała względem dowolnej osi jest równy sumie momentu bezwładności J0 względem osi przechodzącej przez środek masy ciała oraz iloczynu masy tego ciała i kwadratu odległości a obu osi.

J = J
+ ma
Dowód:

Mnożąc obie strony tej zależności przez elementarną masę i całkując po objętości całego ciała otrzymujemy

Korzystając z definicji osiowego momentu bezwładności oraz z definicji środka masy ciała (1.1) mamy, w naszym przypadku

W ten sposób uzyskaliśmy zależność wyrażającą twierdzenie Steinera

3. Napisać transformację Lorentza, wyprowadzić wzór na relatywistyczną dylatację czasu: y = y', z = z'

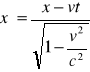
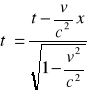
Wyprowadzenie wzoru na relatywistyczną dylatację czasu:

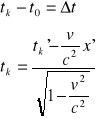
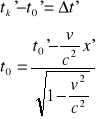
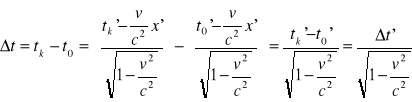
4. Podać definicję oporu elektrycznego, oporu właściwego, prawo Ohma, narysować orientacyjne wykresy zależności oporu właściwego od temperatury dla metali normalnych i nadprzewodzących:

Opór elektryczny (rezystancja): jest miarą oporu czynnego, z jakim element przeciwstawia się przepływowi prądu elektrycznego i wyraża się wzorem R=U/I. Rezystancję oznacza się symbolem R, jednostką rezystancji w układzie SI jest ohm (1 Ω).

Opór właściwy (rezystywność): to miara oporu z jakim materiał o danych wymiarach przeciwstawia się przepływowi prądu elektrycznego. Rezystywność jest zazwyczaj oznaczana jako ρ (ro). Jednostką rezystywności w układzie SI jest om*metr (1 Ωm).
Rezystywność określa wzór na zależność rezystancji przewodnika od jego wymiarów:

=>
,

Prawo Ohma: I~U, czyli U/I=const

5. Opisać silnik Carnota i cykl Carnota , podać wzory na jego sprawność:

Cykl Carnota - obieg termodynamiczny, złożony z dwóch przemian izotermicznych i dwóch przemian adiabatycznych, odwracalny.

Spreż. izoterm - czynnik roboczy styka się z chłodnicą, ma temperaturę chłodnicy i zostaje poddany procesowi sprężania w tej temperaturze (T2). Czynnik roboczy oddaje ciepło do chłodnicy.

Sprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem, jest poddawany sprężaniu aż uzyska temperaturę źródła ciepła (T1).

Rozprężanie izotermiczne - czynnik roboczy styka się ze źródłem ciepła, ma jego temperaturę i poddawany jest rozprężaniu izotermicznemu w temperaturze T1, podczas tego cyklu ciepło jest pobierane ze źródła ciepła.

Rozprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem i jest rozprężany aż czynnik roboczy uzyska temperaturę chłodnicy (T2).

6. Dla wektora indukcji magnetycznej B napisać jego definicję i prawo Gaussa , następnie prawo Ampera i prawo Biota-Savarta z odpowiednimi rysunkami:

Wektor indukcji: B [T=N/(A·m)] jest to wektor styczny do linii indukcji w każdym punkcie i charakteryzujący pole

Fmax - siła jest maksymalna gdy ładunek próbny porusza się pod kątem prostym do B.

7. Omówić efekt Halla: zrobić rysunki i wyprowadzić wzór na napięcie Halla:

Efekt Halla, polega na tym, że w przewodniku z prądem umieszczonym w polu magnetycznym powstaje poprzeczne do prądu i pola magnetycznego napięcie elektryczne.

Wyprowadzenie wzoru na napięcie Halla:

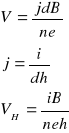
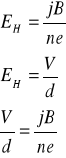
Gdzie: n - koncentracja nośników,

e - ładunek nośnika prądu (ładunek elementarny)

h - grubość płytki, wymiar w kierunku pola magn.,

i - natężenie prądu, R - stała zależna od materiału.

Potencjał V_H, powstały między ściankami przewodnika, nazywany jest potencjałem Halla. Efekt Halla umożliwia pomiar znaku ładunków poruszających się w przewodniku, ich koncentrację.

8. Napisać równanie fali płaskiej harmonicznej

Równanie fali harmonicznej płaskiej (biegnącej) ma postać:

s = A sin (ω t - k x + φ₀)

λ - długość fali; φ₀ - faza początkowa; A - amplituda fali
ω  - częstość kołowa; T - okres drgań; f - częstotliwość 
k - liczba falowa

9. wyprowadzić prawo zachowania pędu dla punktu materialnego:

ZASADA ZACHOWANIA PĘDU (wyprowadzenie):

Zmiana pędu następuje w wyniku działania na ciało siły przez pewien czas. Iloczyn siły i czasu jej działania nazywany jest popędem siły (I).

Jeżeli w układzie inercjalnym na ciało nie działa siła, lub działające siły równoważą się:
to całkowity pęd ciała nie zmienia się:

10. Podać definicję ruchu harmonicznego prostego

Definicja: Ruch harmoniczny jest to ruch drgający w którym przyśpieszenie w każdym punkcie jest wprost proporcjonalne do wychylenia z położenia równowagi, a wychylenia ciała opisywane są funkcją sinusoidalną zależną od czasu.

11. Napisać transformację Lorentza i wyprowadzić z niej relatywistyczne prawo dodawania prędkości(pkt 3):

12. Podać prawo Archimedesa, prawo Pascala,równanie ciągłości strumienia cieczy i równanie Bernoulliego:

Prawo Archimedesa: Ciało w całości lub częściowo zanurzone w płynie jest wypierane ku górze siłą równą ciężarowi wypartego przez to ciało płynu

F_wyporu = m_{płynu *} g = ρ_płynu * g * V

Prawo Pascala: ciśnienie zewnętrzne wywierane na zamknięty w zbiorniku płyn jest przekazywane niezmiennie na każdą część płynu oraz na ścianki naczynia

Równanie ciągłości strumienia:

Δm₁=ρS₁V₁Δt Δm₂=ρS₂V₂Δt

Δm₁= Δm₂ => ρS₁V₁Δt=ρS₂V₂Δt => ρSV=const.

Prawo ciągłości strumienia cieczy - mówi, że przez każdy przekrój naczynia w tym samym czasie przepływa taka sama objętość cieczy, czyli przepływ jest stały i niezależny od przekroju naczynia.

13. Omówić powst. fali stojącej, obliczyć współrzędne węzłów i strzałek

Fala stojąca: Fala stojąca może zostać wytworzona w ośrodku poruszającym się względem obserwatora lub w przypadku interferencji dwóch fal poruszających się w przeciwnych kierunkach.Cząstki ośrodka drgają ruchem harmonicznym prostym ale różne punkty mają różną amplitudę drgań zależną od ich położenia.

Powstawanie w wyniku interferencji dwóch fal poruszających się w przeciwnych kierunkach:

y₁=Asin(kx-ωt), y₂=Asin(kx+ωt)

Superpozycja: y=y₁+y₂=2Asin(kx)cos(ωt)

Współrzędne węzłów i strzałek:

gdy kx = (π/2, 3π/2, 5π/2…) czyli x = (λ/4, 3λ/4, 5λ/4) - A=max - są to STRZAŁKI;

gdy kx=(π, 2π, 3π…), czyli (x = λ/2, λ, 3λ/2) - A=0 -węzły

Energia w tej fali nie jest przenoszona bo węzły mają Ek i Ep = 0, => jest magazynowana w poszczególnych odcinkach ośrodka.

14. Napisać transformację Lorentza (4 pkt.), obliczyć relatywistyczne skrócenie długości:

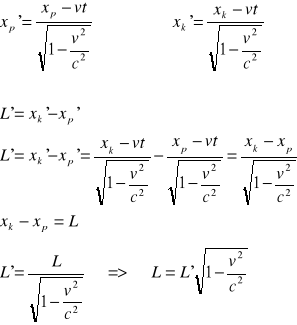
15.Omówić krótko wytwarzanie fali elektromagnetycznej, podać dwie istotne cechy fali el-magn, opisać widmo fal elektromagnetycznych:

Fala elektromagnetyczna: rozchodzące się w przestrzeni zaburzenie pola elektromagnetycznego; zaburzenie to ma charakter fali poprzecznej w której składowa elektryczna i magnetyczna, prostopadłe do siebie i kierunku ruchu, nawzajem się przekształcają. Zmieniające się pole elektryczne E wytwarza pole magnetyczne B, a zmieniające się pole magnetyczne wytwarza pole elektryczne. Cechy fali elektromagnetycznej:

- rozchodzi się w próżni z prędkością światła c;

- zdolność do przenoszenia energii od punktu do punktu;

- są falami poprzecznymi więc mogą podlegać polaryzacji;

- przenikają przez dielektryk a odbijają się od metalu

WIDMO FAL ELEKTROMAGNETYCZNYCH: zestawienie fal elektromagnetycznych według ich częstotliwości.

Jeżeli wiązkę promieniowania przepuścimy przez układ rozszczepiający, to wówczas na "ekranie" otrzymamy widmo:
- liniowe - dają poszczególne pierwiastki i obserwujemy go w postaci prążków
- pasmowe - tworzy pasma barwne
- ciągłe - tworzą kolejne barwy przechodząc jedna w drugą bez przerwy. barwy zmieniają się od czerwonej do fioletu.

16 ferromagnetyzm, przykłady metali ferromagnet. ferromagnetyzm - zjawisko, polegające na samorzutnym , spontanicznym namagnesowaniu się substancji

przykłady:Fe(zelazo), Co(kobalt), Ni(nikiel)

17.prawo załamania, zasada Huygensa i zasadę Fermata, Prawo załamania: promień padający P pochodzący z ośrodka 1, w punkcie S pada na granicę ośrodków, załamuje się na granicy i podąża jako promień załamany Z w ośrodku 2. Promienie padający i załamany oraz normalna leżą w jednej płaszczyźnie a kąty spełniają zależność:

Gdzie: n1 — wspł załamania światła ośrodka 1;

* n2 — współczynnik załamania światła ośrodka 2

* θp — kąt padania, kąt między promieniem padającym a prostopadłą padania,

* θz — kąt załamania, kąt między promieniem załamanym a prostopadłą padania.

Zasada Fermata: Promień świetlny poruszający się (w dowolnym ośrodku) od punktu A do punktu B przebywa zawsze lokalnie ekstremalną drogę optyczną, czyli taką, na której przebycie potrzeba czasu najkrótszego, bądź najdłuższego z możliwych.

Zasada Huygensa: każdy punkt czoła fali można uważać za źródło nowej fali kulistej. Wypadkową powierzchnię falową tworzy powierzchnia styczna do wszystkich powierzchni fal cząstkowych

18. potencjał pola grawitacyjnego:

Potencjał pola:

19. prawo Gaussa i związek z Coulombem

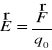
Prawo Gaussa: strumień natężenia pola elektrycznego przenikający przez dowolną powierzchnię zamkniętą w jednorodnym środowisku o bezwzględnej przenikalności dielektrycznej ε, jest równy stosunkowi całkowitego ładunku znajdującego się wewnątrz tej powierzchni do wartości tejże przenikalności.

Związek między nimi:

Ze wzoru:
wynika że pole wektorowe
jest polem źródłowym. Dla ładunku punktowego q pole ma symetrię sferyczną, dzięki czemu strumień pola w odległości R można zapisać jako:

gdzie S_R jest powierzchnią kuli w n-wymiarowej przestrzeni. Z powyższego wynika:

Powierzchnia kuli jest równa 4πR², dlatego:

Otrzymane równanie wyraża prawo Coulomba

---