1. 
   Liczba interwencji technika w ciągu godziny pracy pewnego automatu ma następujący rozkład:

Liczba interwencji	Prawdopodobieństwa
0	0,3844
1	0,4712
2	0,1444

Proszę obliczyć charakterystyki rozkładu z kwartylami włącznie.

2. Wyznacz wartość oczekiwaną i wariancję zmiennych:

1. Y=2X+1

2. Z=X²

3. W= - X²+2

Jeśli E(X)=2 ; D²(X)=V(X)=1; E(X⁴)=34

3. Dystrybuanta zmiennej losowej X jest określona następująco:

X<x	X<-5	X<-3	X<-1	X<1	X<4	X<n, n>4
F(x)	0	0,111	0,285	0,580	0,940	1,000

Wyznaczyć prawdopodobieństwa:

1. P(X ≥ -2)

2. P(X < 2)

3. P(-3 < X <1)

4. P(0 ≤ X ≤ 4)

5. P(-7 < X < -4)

6. P(X = -1)

7. P(X = 2)

4. Dla zmiennej losowej o rozkładzie Poissona P(1)=0,1815 ; P(2)=0,2450. Wyznacz parametry rozkładu zmiennej (wraz z dominantą) i P(X>0).

5. W urnie jest 15 kul białych, 80 niebieskich i 5 czerwonych. Gracz po wpłaceniu 100 zł losuje najpierw jedną kulę i jeżeli jest to kula czerwona to kończy grę (przegrywa). W przeciwnym razie losuje drugą kulę (nie zwracając pierwszej) i jeżeli jest tego samego koloru co kula pierwsza, to wygrywa: za dwie niebieskie 200 zł, za dwie białe 300 zł. Jeżeli druga wylosowana kula jest inna, niż pierwsza to wygrana zależy od jej koloru: gdy druga jest biała lub niebieska gracz wygrywa 100 zł, gdy jest czerwona 50 zł.

1. Zdefiniuj zmienną losową opisującą wynik gry, znajdź jej rozkład i dystrybuantę.

2. Wyznacz: wartość oczekiwaną, współczynnik zmienności.

3. 
   Jakie są szanse, że w dwóch próbach (każda jak wyżej) wygrana będzie większa od 10 zł ?

1. 
   Liczba interwencji technika w ciągu godziny pracy pewnego automatu ma następujący rozkład:

Liczba interwencji	Prawdopodobieństwa
0	0,3721
1	0,4758
2	0,1521

Proszę obliczyć charakterystyki rozkładu z kwartylami włącznie.

2. Wyznacz wartość oczekiwaną i wariancję zmiennych:

1. Y= -2,5X-1

2. Z=X²

3. W= - X²-5

Jeśli E(X)=3 ; D²(X)=V(X)=2; E(X⁴)=140

3. Dystrybuanta zmiennej losowej X jest określona następująco:

X<x	X<-5	X<-3	X<-1	X<1	X<4	X<n, n>4
F(x)	0	0,080	0,275	0,593	0,81	1,000

Wyznaczyć prawdopodobieństwa:

1. P(X ≥ -2)

2. P(X < 2)

3. P(-3 < X <1)

4. P(0 ≤ X ≤ 4)

5. P(-7 <X < -4)

6. P(X = -1)

7. P(X = 2)

4. Dla zmiennej losowej o rozkładzie Poissona P(3)=0,2046 ; P(4)=0,1944. Wyznacz parametry rozkładu zmiennej (wraz z dominantą) i P(X>0).

5. W urnie jest 20 kul białych, 70 niebieskich i 10 czerwonych. Gracz po wpłaceniu 100 zł losuje najpierw jedną kulę i jeżeli jest to kula czerwona to kończy grę (przegrywa). W przeciwnym razie losuje drugą kulę (nie zwracając pierwszej) i jeżeli jest tego samego koloru co kula pierwsza, to wygrywa: za dwie niebieskie 200 zł, za dwie białe 300 zł. Jeżeli druga wylosowana kula jest inna, niż pierwsza to wygrana zależy od jej koloru: gdy druga jest biała lub niebieska gracz wygrywa 100 zł, gdy jest czerwona 50 zł.

1. Zdefiniuj zmienną losową opisującą wynik gry, znajdź jej rozkład i dystrybuantę.

2. Wyznacz: wartość oczekiwaną, współczynnik zmienności.

3. Jakie są szanse, że w dwóch próbach (każda jak wyżej) wygrana będzie większa od 10 zł ?




1. Liczba interwencji technika w ciągu godziny pracy pewnego automatu ma następujący rozkład:

Liczba interwencji	Prawdopodobieństwa
0	0,6084
1	0,3432
2	0,0484

Proszę obliczyć charakterystyki rozkładu z kwartylami włącznie.

2. Wyznacz wartości oczekiwane zmiennych Z i W oraz wariancję zmiennej Z:

Jeśli Z = 3X - 2Y ; W = X²- Y² oraz E(X) = -3 ; E(Y)= 4; D²(X)=V(X)=0,5 ; D²(Y)=V(Y)=2.

3. Dystrybuanta zmiennej losowej X jest określona następująco:

X<x	X<-5	X<-3	X<-1	X<1	X<4	X<n, n>4
F(x)	0	0,352	0,838	0,930	0,979	1,000

Wyznaczyć prawdopodobieństwa:

1. P(X ≥ -2)

2. P(X < 2)

3. P(-3 < X < 1)

4. P(0 ≤ X ≤ 4)

5. P(-7 < X < -4)

6. P(X = -1)

7. P(X = 2)

4. Dla zmiennej losowej o rozkładzie Poissona trzeci moment centralny standaryzowany wynosi 1,4. Wyznacz parametry rozkładu zmiennej (wraz z dominantą), P(X≤ 1), P(X>0).

5. W urnie jest 40 kul białych, 25 niebieskich i 35 czerwonych. Gracz po wpłaceniu 100 zł losuje najpierw jedną kulę i jeżeli jest to kula czerwona to kończy grę (przegrywa). W przeciwnym razie losuje drugą kulę (nie zwracając pierwszej) i jeżeli jest tego samego koloru co kula pierwsza, to wygrywa: za dwie niebieskie 200 zł, za dwie białe 300 zł. Jeżeli druga wylosowana kula jest inna, niż pierwsza to wygrana zależy od jej koloru: gdy druga jest biała lub niebieska gracz wygrywa 100 zł, gdy jest czerwona 50 zł.

1. Zdefiniuj zmienną losową opisującą wynik gry, znajdź jej rozkład i dystrybuantę.

2. Wyznacz: wartość oczekiwaną, współczynnik zmienności.

3. Jakie są szanse, że w dwóch próbach (każda jak wyżej) wygrana będzie większa od 10 zł ?




1. 
   Liczba interwencji technika w ciągu godziny pracy pewnego automatu ma następujący rozkład:

Liczba interwencji	Prawdopodobieństwa
0	0,4489
1	0,4422
2	0,1089

Proszę obliczyć charakterystyki rozkładu z kwartylami włącznie.

2. Wyznacz wartości oczekiwane zmiennych Z i W oraz wariancję zmiennej Z:

Jeśli Z= 3X - 2Y ; W = X²- Y² oraz E(X) = -4; E(Y) = 3; D²(X)=V(X)=2 ; D²(Y)=V(Y)=0,5.

3. Dystrybuanta zmiennej losowej X jest określona następująco:

X<x	X<-5	X<-3	X<-1	X<1	X<4	X<n, n>4
F(x)	0	0,113	0,244	0,729	0,982	1,000

Wyznaczyć prawdopodobieństwa:

1. P(X ≥ -2)

2. P(X < 2)

3. P(-3 < X <1)

4. P(0 ≤ X ≤ 4)

5. P(-7 < X < -4)

6. P(X = -1)

7. P(X = 2)

4. Dla zmiennej losowej o rozkładzie Poissona czwarty moment centralny standaryzowany wynosi 0,16. Wyznacz parametry rozkładu zmiennej (wraz z dominantą), P( X ≤ 1 ), P(X > 0).

5. W urnie jest 15 kul białych, 45 niebieskich i 40 czerwonych. Gracz po wpłaceniu 100 zł losuje najpierw jedną kulę i jeżeli jest to kula czerwona to kończy grę (przegrywa). W przeciwnym razie losuje drugą kulę (nie zwracając pierwszej) i jeżeli jest tego samego koloru co kula pierwsza, to wygrywa: za dwie niebieskie 200 zł, za dwie białe 300 zł. Jeżeli druga wylosowana kula jest inna, niż pierwsza to wygrana zależy od jej koloru: gdy druga jest biała lub niebieska gracz wygrywa 100 zł, gdy jest czerwona 50 zł.

1. Zdefiniuj zmienną losową opisującą wynik gry, znajdź jej rozkład i dystrybuantę.

2. Wyznacz: wartość oczekiwaną, współczynnik zmienności.

3. Jakie są szanse, że w dwóch próbach (każda jak wyżej) wygrana będzie większa od 10 zł ?




1. Liczba interwencji technika w ciągu godziny pracy pewnego automatu ma następujący rozkład:

Liczba interwencji	Prawdopodobieństwa
0	0,5476
1	0,3848
2	0,0676

Proszę obliczyć charakterystyki rozkładu z kwartylami włącznie.

2. Wyznacz wartości oczekiwane i odchylenia standardowe zmiennych Z i W, jeśli Z=3X+2 ; W= -X-Y ; E(X) = -2; E(Y) = 1; D²(X)= V(X)= 5 ; D²(Y)= V(Y) = 1.

3. Z obserwacji wynika, że 30% nowych samochodów określonej marki i typu wymaga drobnych napraw w ciągu pierwszych sześciu miesięcy użytkowania. Wiedząc, że salon sprzedał 5 nowych aut, wyznacz:

1. rozkład zmiennej losowej opisującej liczbę napraw,

2. wartość oczekiwaną, odchylenie standardowe, trzeci i czwarty moment centralny standaryzowany,

3. prawdopodobieństwo, że żaden z samochodów nie będzie wymagał naprawy

4. prawdopodobieństwo, że co najmniej 3 samochody będą wymagały naprawy.

4. Dla zmiennej losowej o rozkładzie Poissona V_ZK=40%. Wyznacz parametry rozkładu zmiennej (wraz z dominantą), P(X≤ 1), P(X >0).

5. Obciążona moneta (prawdopodobieństwo wyrzucenia orła wynosi 0,3) jest rzucana, aż do pojawienia się orła. Liczba rzutów jest ograniczona do trzech. Zmienną losową jest numer rzutu, w którym osiągnięto orła (jeśli trzy razy pod rząd wystąpią reszki to zmienna losowa ma wartość zero). Wyznacz:

1. rozkład prawdopodobieństwa zmiennej ,

2. dystrybuantę,

3. dominantę.




1. 
   Liczba interwencji technika w ciągu godziny pracy pewnego automatu ma następujący rozkład:

Liczba interwencji	Prawdopodobieństwa
0	0,4624
1	0,4352
2	0,1024

Proszę obliczyć charakterystyki rozkładu z kwartylami włącznie.

2. Wyznacz wartości oczekiwane i odchylenia standardowe zmiennych Z i W, jeśli Z=7+2Y ; W=2X - 3Y oraz E(X) = -1; E(Y) = 10; D²(X) =V (X) = 4 ; D²(Y) = V(Y) = 8.

3. Z obserwacji wynika, że 20% nowych samochodów określonej marki i typu wymaga drobnych napraw w ciągu pierwszych sześciu miesięcy użytkowania. Wiedząc, że salon sprzedał 5 nowych aut, wyznacz:

1. rozkład zmiennej losowej opisującej liczbę napraw,

2. wartość oczekiwaną, odchylenie standardowe, trzeci i czwarty moment centralny standaryzowany,

3. prawdopodobieństwo, że żaden z samochodów nie będzie wymagał naprawy

4. prawdopodobieństwo, że co najwyżej 3 samochody będą wymagały naprawy.

4. Dla zmiennej losowej o rozkładzie Poissona odchylenie standardowe wynosi 2,5. Wyznacz pozostałe parametry rozkładu zmiennej (wraz z dominantą), P(X≤ 1), P(X>0).

5. Obciążona moneta (prawdopodobieństwo wyrzucenia orła wynosi 0,4) jest rzucana, aż do pojawienia się orła. Liczba rzutów jest ograniczona do trzech. Zmienną losową jest numer rzutu, w którym osiągnięto orła (jeśli trzy razy pod rząd wystąpią reszki to zmienna losowa ma wartość zero). Wyznacz:

1. rozkład prawdopodobieństwa zmiennej ,

2. dystrybuantę,

3. dominantę.




Statystyka matematyczna, kolokwium 1

39

28 kwietnia 2009 r.

WZORY:















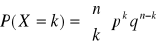
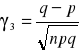
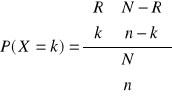
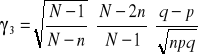
WZORY:















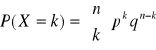
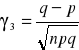
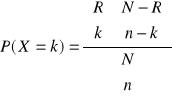
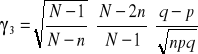
WZORY:















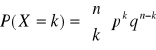
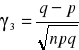
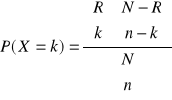
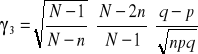
WZORY:















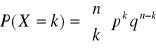
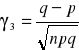
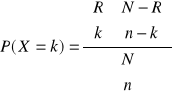
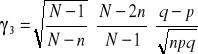
WZORY:















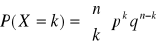
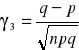
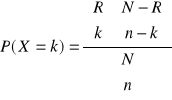
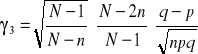
WZORY:















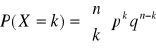
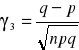
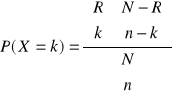
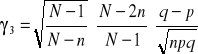
IMIĘ I NAZWISKO RODZAJ STUDIÓW

IMIĘ I NAZWISKO RODZAJ STUDIÓW

IMIĘ I NAZWISKO RODZAJ STUDIÓW

IMIĘ I NAZWISKO RODZAJ STUDIÓW

IMIĘ I NAZWISKO RODZAJ STUDIÓW

IMIĘ I NAZWISKO RODZAJ STUDIÓW

---