ZADANIA DO SAMODZIELNEGO ROZWIĄZANIA (cz.1 równowaga układów sił bez tarcia)

Zadanie1 Obliczyć reakcje podpór A i B w belce pokazanej na rysunku. Obciążenie zewnętrzne stanowią dwie siły P₁ = 200 N, P₂ = 100 N i moment M = 200 N · m. Pozostałe dane liczbowe wynoszą:

l = 1 m, = 45º,  = 30º.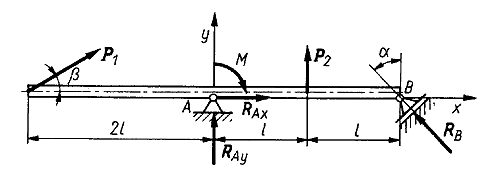



R o z w i ą z a n i e.
                R_A= 350,77N   R_B=212,13N

Zadanie2 Belka AB o ciężarze G = 10 kN jest utwierdzona na końcu A i obciążona momentem

M = 20 kNm i obciążeniem ciągłym q = 1 kN/m (rys.). Do końca B jest przymocowana wiotka linka, która jest przerzucona przez idealny krążek (bez tarcia) i obciążona ciężarem P = 5 kN. Obliczyć reakcje w podporze A, jeżeli b = 2 m i α = 30^o.

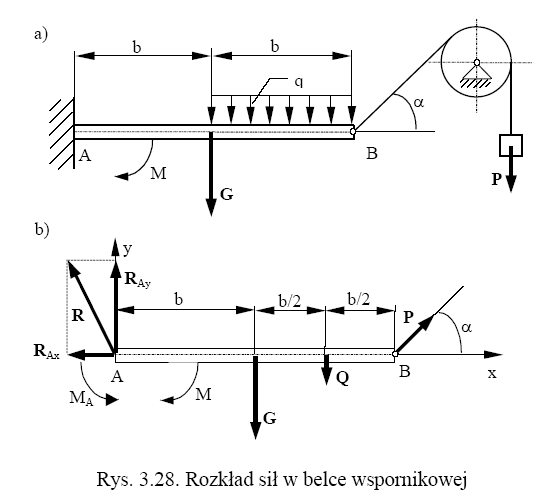
Rozwiązanie.

R_A= 10,44 kN, M_A   = 36kNm

Zadanie3

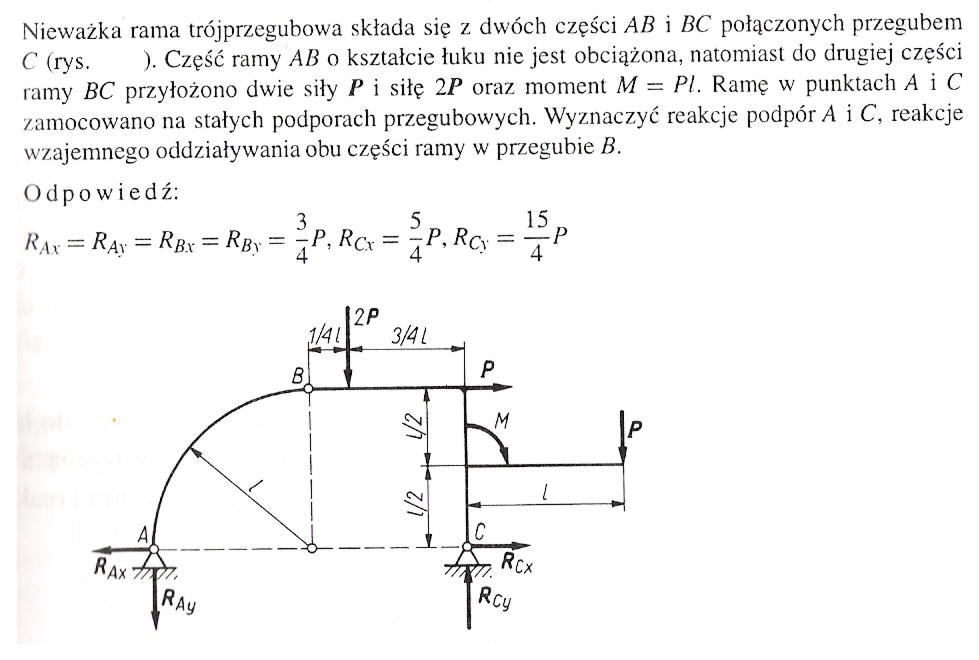
Zadanie4

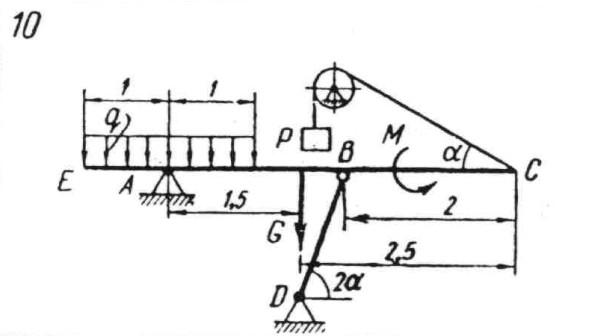
Wyznaczyć reakcje podporowe w układach przedstawionym na poniższych schematach:

G = 12 [kN]
P = 8 [kN]
M = 10 [kNm]
q = 4 [kN/m]

ဠၡ =30^o

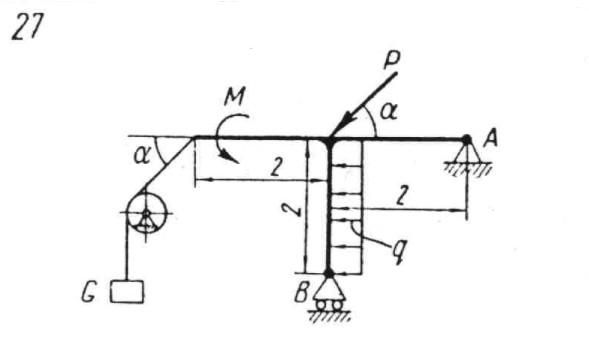
P = 4 [kN]
M = 7 [kNm]
q = 0,5 [kN/m]
ဠၡ =30^o

G = 5 [kN]
P = 4 [kN]
M = 8 [kNm]
q = 2,5 [kN/m]
ဠၡ=45^o

G = 4 [kN]
P = 4 [kN]
M = 4 [kNm]
q = 2 [kN/m]
ၡ =60^o

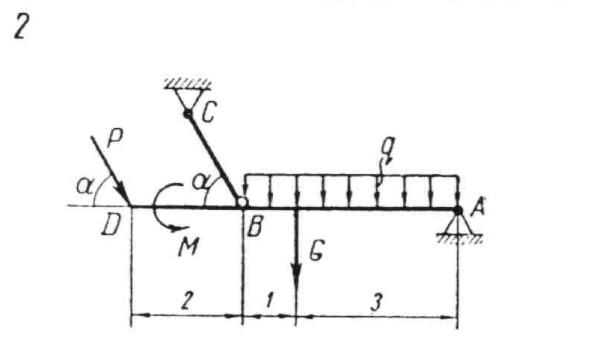
Zadanie5

Wyznaczyć reakcje stałych podpór przegubowych A i B oraz przegubu C w ramie łukowej o promieniu R=4m, którą obciążono siłami P1= 350N , P2= 150N. Kierunek działania siły P1 określa kat α= 15^o, siła P2 jest pozioma i odległa od punku A o h=1,8m.

R o z w i ą z a n i e

R_C=R_B=286,8 N, R_A= 140,5 N.

---