Politechnika Rzeszowska im. Ignacego Łukasiewicza

Wydział Elektrotechniki i Informatyki

Teoria obwodów

Projekt

Zaprojektować filtr dolnoprzepustowy Czebyszewa

Konsultował: Wykonali:

dr inż. Grzegorz Masłowski Łukasz Januszewski

Prof. PRZ Tomasz Gałecki

1. Główne cele

1. Głównie cele

1. Poznanie wiadomości dotyczących filtrów

2. Projekt filtru cyfrowego

• Określenie parametrów filtru cyfrowego

• Wyznaczenie pulsacji granicznych filtru analogowego

• Wyznaczenie parterów unormowanego dolnoprzepustowego filtru analogowego

• Projektowanie prototypowego filtru dolnoprzepustowego Czebyszewa

• Wyznaczenie rzędu N filtru

• Obliczenie biegunów filtru prototypowego

• Wyznaczenie transmitancji filtru prototypowego

- Dokonanie transformacji częstotliwości filtru prototypowego

- Wyznaczenie charakterystyk częstotliwościowych i czasowych

• Wyznaczenie transmitancji filtru cyfrowego

• Wyznaczenie charakterystyk częstotliwościowych i odpowiedzi impulsowej

2. Wnioski i spostrzeżenia

3. WSTĘP TEORETYCZNY

Filtry aktywne są stosowane we wszystkich dziedzinach elektrotechniki . Mają spełniać zadania podobne do zadań filtrów pasywnych . Użycie elementów aktywnych pozwala zrezygnować z cewek indukcyjnych , sprawiających wiele uciążliwości . Można w związku z tym budować układy lżejsze i o lepszych własnościach elektrycznych .Należy jednak zwrócić uwagę na stabilność , ponieważ mogą generować szkodliwe drgania . Przyczyną ich są zazwyczaj niewielkie zmiany

parametrów , spowodowane na przykład warunkami zewnętrznymi ( np. zmiany temp. )

Filtry aktywne różnią się od filtrów pasywnych występowaniem źródeł sterowanych oraz pracą przy w miarę dowolnym (niekoniecznie dopasowanym) obciążeniu . Opis filtrów aktywnych można ograniczyć do filtrów dolnoprzepustowych , ponieważ można je za pomocą transformacji częstotliwości

Przekształcić w filtry górnoprzepustowe , pasmowoprzepustowe oraz pasmowozaporowe .

Problem syntezy transmitancji filtrów aktywnych można rozwiązać za pomocą połączenia łańcuchowego układów pierwszego i drugiego rzędu . W syntezie dowolnej impedancji , będącej funkcją wymierną , wystarczy rozłożyć ją na iloczyn funkcji wymiernych elementarnych i każdy czynnik zrealizować za pomocą czwórnika aktywnego . Zastosowanie czwórników aktywnych zapewnia spełnienie warunku wzajemnego nieobciążania się sekcji połączenia łańcuchowego .

Charakterystyki częstotliwościowe można optymalizować z różnych teoretycznych punktów widzenia . Z takich przesłanek optymalizacyjnych wynikają określone wartości współczynników a_i i b_i . Powstają przy tym sprzężone bieguny zespolone , których nie można zrealizować za pomocą biernych układów RC . Uzyskanie sprzężonych biegunów zespolonych staje się możliwe w wyniku zastosowania układów LRC . W zakresie częstotliwości dużych realizacja żądanych indukcyjności nie sprawia żadnych trudności , natomiast w zakresie małych częstotliwości przeważnie są potrzebne duże indukcyjności , które są bardzo niewygodne i mają złe własności elektryczne . Można jednak uniknąć stosowania takich indukcyjności dla zakresu częstotliwości małych , jeżeli do układów RC doda się elementy aktywne ( wzmacniacze operacyjne ) .Takie układy określa się mianem filtrów aktywnych .

Ogólna postać charakterystyki częstotliwościowej filtru dolnoprzepustowego przedstawia się następująco :

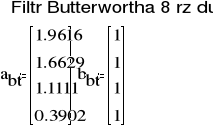
(1.1)

gdzie bi może być równe 0 , ai , bi rzeczywiste

Rząd filtru jest równy najwyższej potędze S . Dla realizacji filtru jest korzystne , aby wielomian dawał się rozłożyć na czynniki . Jeśli dopuszcza się również składniki zespolone , wtedy nie jest możliwe rozłożenie na czynniki liniowe i otrzymuje się iloczyn wyrażeń kwadratowych .

1. PORÓWNANIE ZOPTYMALIZOWANYCH CHARAKTERYSTYK FILTRÓW

AKTYWNYCH

Charakterystyka częstotliwościowa filtrów dolnoprzepustowych Butterwortha przebiega w znacznym zakresie poziomo załamując się ostro dopiero przed osiągnięciem częstotliwości granicznej . Odpowiedź skokowa charakteryzuje się znacznymi drganiami , które rosną wraz ze wzrostem rzędu filtru .

Najbardziej stromy spadek wzmocnienia powyżej częstotliwości granicznej ma filtr dolnoprzepustowy Czebyszewa .Jednakże przebieg wzmocnienia w zakresie częstotliwości przenoszonych nie jest monotoniczny ; występuje tu pewne zafalowanie . Drgania w odpowiedzi skokowej filtru są jeszcze większe niż w przypadku filtru Butterwotha .

Optymalną odpowiedź skokową ma filtr dolnoprzepustowy Bessla . Obowiązuje przy tym założenie , opóźnienie ma wartość stałą w możliwie dużym zakresie częstotliwości , tzn. że dla zakresu częstotliwości przesunięcie fazowe jest proporcjonalne do częstotliwości . Zauważmy jednak , że charakterystyka częstotliwościowa filtru Bessla nie ma takiego ostrego załamania jak ma to miejsce w przypadku filtrów Butterwortha czy Czebyszewa .

Przykładowe charakterystyki filtrów dolnoprzepustowych Czebyszewa , Butterwortha , Bessla :

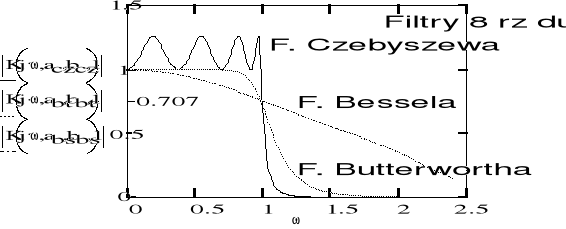
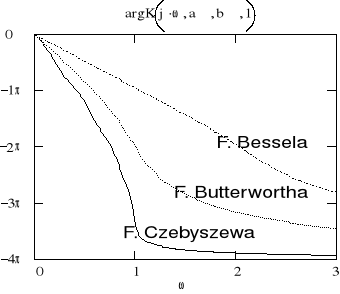
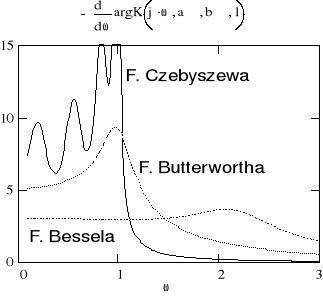
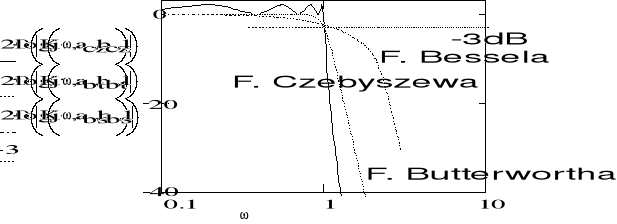
Łatwo zauważyć , że najbardziej strome przejście od pasma przepustowego do pasma tłumieniowego ma filtr Czebyszewa . Okupuje się to zafalowaniem charakterystyki częstotliwościowej w paśmie przepustowym . Im mniejsze jest to zafalowanie , tym bardziej właściwości filtru Czebyszewa są podobne do właściwości filtru Butterwortha . Obydwa filtry charakteryzują się znacznymi oscylacjami w ich odpowiedzi skokowej . Filtry Bessla dają tylko minimalne drganie . Mimo ich niezbyt dobrej charakterystyki częstotliwościowej stosuje się je zawsze tam , gdzie jest wymagana optymalna odpowiedź na wymuszenie skokowe .

2. FILTRY DOLNOPRZEPUSTOWE CZEBYSZEWA

Przy małych częstotliwościach wzmocnienie filtrów dolnoprzepustowych Czebyszewa jest równe k_u0 .To wzmocnienie zmniejsza się jednak już poniżej częstotliwości granicznej , zgodnie z określoną falistością daną z góry , Wielomiany wykazujące w pewnym zakresie stałą falistość są wielomiany Czebyszewa :

T_n(x) : cos(n arccosx) dla 0
x
1 (1.2)

cos(n arccosh) dla x > 1

W zakresie 0
x
1 wielomian
oscyluje między 0 i 1 a dla x > 1 rośnie monotonicznie . Dla uzyskania równania filtru dolnoprzepustowego z wielomianów Czebyszewa przyjmujemy

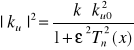
(1.3)

Stałą k dobiera się tak by dla x=0 kwadrat modułu funkcji przenoszenia
² był równy k_u0² tzn. dla n nieparzystych k=1 a dla n parzystych k=1+ε² , gdzie współczynnik ε=<1 jest miarą falistości.

Z modułu wzmocnienia można wyliczyć wzmocnienie zespolone i stąd wyznaczyć współczynniki . Można bieguny wzmocnienia zespolonego obliczyć bezpośrednio z biegunów filtru Butterwortha . Stąd w wyniku obliczenia sprzężonych biegunów zespolonych otrzymuje się współczynniki a_i i b_i w równaniu (1.1) zgodnie z następującymi zależnościami :

Rząd n parzysty :

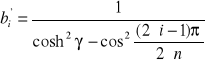
(1.4)

(1.5)

dla

Rząd n nieparzysty :

(1.6)

(1.7)

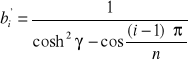
(1.8)

(1.9)

dla

przy czym

Jeśli otrzymane w ten sposób współczynniki a_i i b_i podstawimy do równania (1.1) to otrzymamy filtr Czebyszewa , w którym wartość S nie jest znormalizowana względem częstotliwości ω_g( 3 dB ) , lecz względem częstotliwości ω_c , przy której wzmocnienie przybiera po raz ostatni wartość k_{u min} .

Łatwo zauważyć , że charakterystyki częstotliwościowe wszystkich filtrów dolnoprzepustowych można przedstawić przy pomocy wyrażenia :

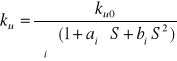
(2.0)

Rząd filtru określony jest najwyższą potęgą S po wykonaniu mnożeń w mianowniku . Ten rząd determinuje asymptotyczny spadek charakterystyki częstotliwościowej wzmocnienia z szybkością -n20dB na dekadę . Pozostała część przebiegu zależy dla danego rzędu od typu filtru .

Dodatkowo częstotliwość graniczna ( 3dB ) każdego takiego ogniwa filtru jest określona przez wielkość ν_gi/ν_g .Ta wielkość nie jest wykorzystywana do obliczeń , ale jest bardzo przydatna , gdyż umożliwia sprawdzenie prawidłowego funkcjonowania poszczególnych ogniw filtru .

PROJEKT FILTRU CYFROWEGO

Parametry filtru cyfrowego:

Częstotliwość próbkowania:

Tłumienie w paśmie przepustowym i zaporowym

Ze względu na zniekształcenie osi częstotliwości prototyp analogowy filtru cyfrowego projektuję według przeliczonej pulsacji granicznej. Posługuję się programem Mathcad 15 do obliczenia wartości współczynników transmitancji filtru.

1.Określenie parametrów filtru cyfrowego:

Obliczenie pulsacji unormowanych

2.Wyznaczenie pulsacji granicznych filtru analogowego:

3.Wyznaczenie parametrów unormowanego dolnoprzepustowego filtru analogowego:

4.Zaprojektowanie dolnoprzepustowego prototypowego filtru unormowanego:

- wyznaczenie rzędu filtru N a także parametru ε

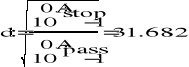
Wyznaczenie rzędu filtru:

- na podstawie parametrów filtru obliczam bieguny filtru prototypowego:

Bieguny filtru:

-wyznaczenie transmitancji filtru prototypowego

Licznik:

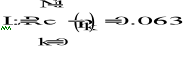
Mianownik:

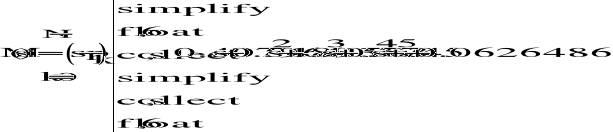
Za pomocą funkcji explicit podstawiamy wartość licznika i mianownika

Transmitancja filtru prototypowego:

5.Dokonanie transformacji częstotliwości filtru prototypowego na filtr analogowy:

- za s podstawiamy:

- licznik i mianownik mnożymy przez

Uzyskujemy transmitancję operatorową filtru analogowego:

6.Wyznaczenie charakterystyk częstotliwościowych (amplitudowa i fazowa), a także czasowe (odpowiedź impulsową i skokową) zaprojektowanego filtru analogowego

Wyznaczenie charakterystyk częstotliwościowych

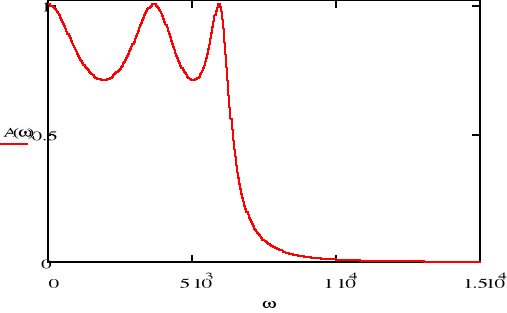
Charakterystyka amplitudowa

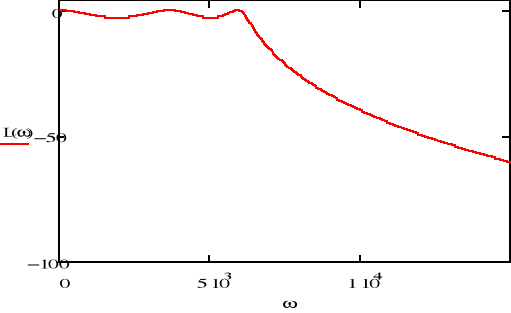
Charakterystyka amplitudowa logarytmiczna

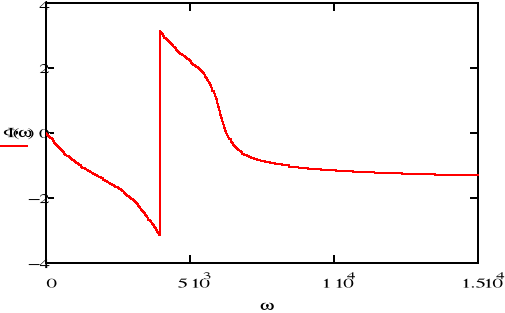
Charakterystyka fazowa

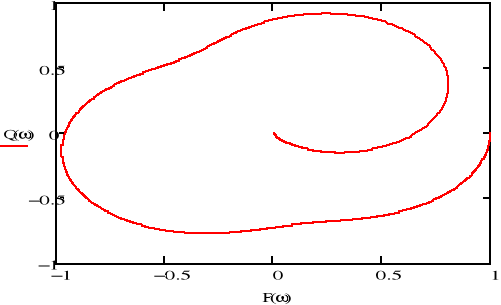
wykres Nyquista

Wyznaczenie charakterystyk czasowych

Odpowiedz impulsowa

Wyznaczenie czasu ustalania

Czas ustalania jest to czas po którym sygnał nie różni się o 5% sygnału wartości w stanie ustalonym

(jest równe od 0.95 - 1.05)

Szacunkowy czas ustalania: ok.
s

Odpowiedz skokowa

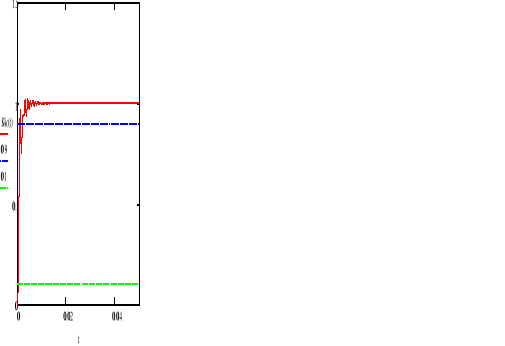
Czas narastania jest czasem sygnału od 0,1 do 0.9 wartości w stanie ustalonym.

Szacunkowy czas narastania:
s

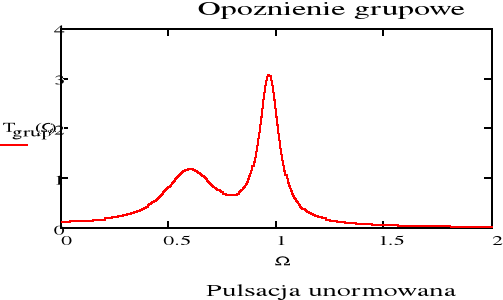
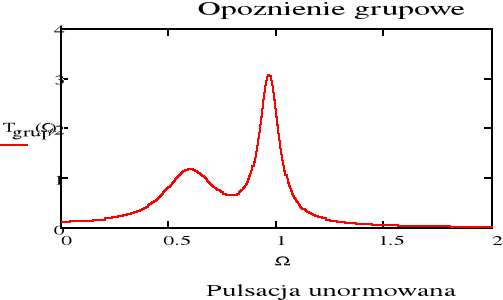
Opóźnienie grupowe

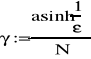
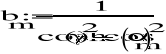
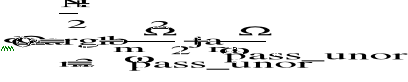
7.Wyznaczenie transmitancji filtru cyfrowego na podstawie transmitancji biliniowej:

-za s podstawiamy

Otrzymujemy transmitancję filtru cyfrowego:

8.Wyznaczenie charakterystyk częstotliwościowych zaprojektowanego filtru cyfrowego:

Wyznaczenie charakterystyk częstotliwościowych

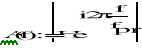
Charakterystyka amplitudowa

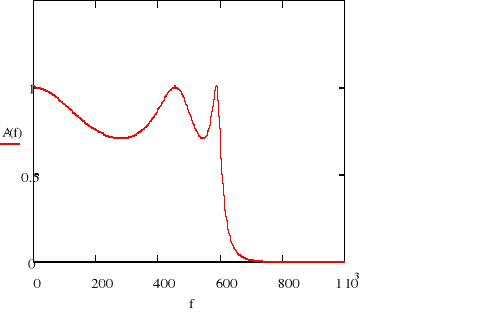
Charakterystyka amplitudowa logarytmiczna

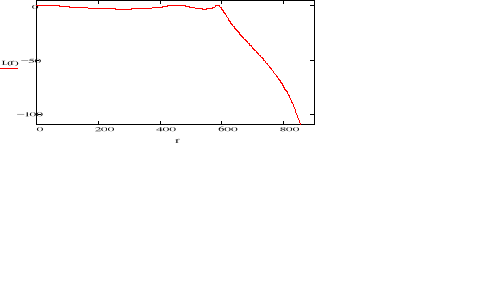
Charakterystyka fazowa

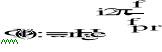
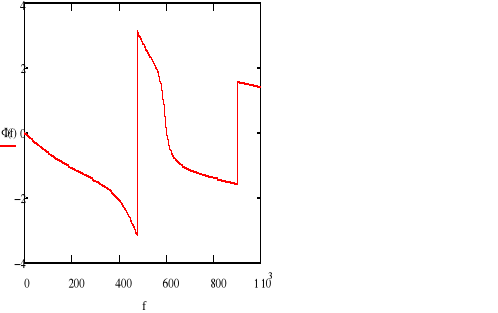
WYDRUK PROGRAMU

Parametry zadane dla projektowanego filtru cyfrowego:

Obliczenie pulsacji unormowanych

Obliczenie pulsacji filtru prototypowego

Wyznaczenie współczynnika

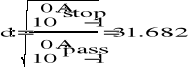
Wyznaczenie rzędu filtru

Obliczenie biegunów transmitancji:

Obliczenie liczniki i mianownika filtru prototypowego

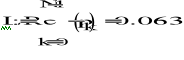
Liczniki jest iloczynem biegunów

Mianowniki iloczynem

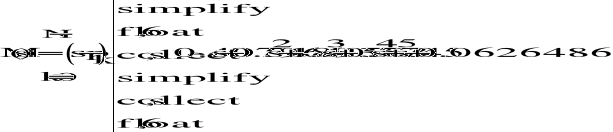
Za pomocą funkcji explicit podstawiamy wartość licznika i mianownika

Obliczenie transmitancji filtru analogowego za pomocą transformacji częstotliwości

Licznik mnożymy razy ω.pass^5

Mianownik mnożymy razy ω.pass^5 a także za s podstawiamy s/ω.pass

Za pomocą funkcji explicit podstawiamy liczniki i mianownik

Ostateczna postać transmitancji filtru analogowego:

Wyznaczenie charakterystyk częstotliwościowych

charakterystyka amplitudowa

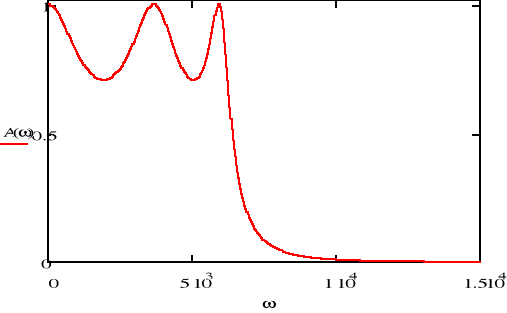
charakterystyka amplitudowa logarytmiczna

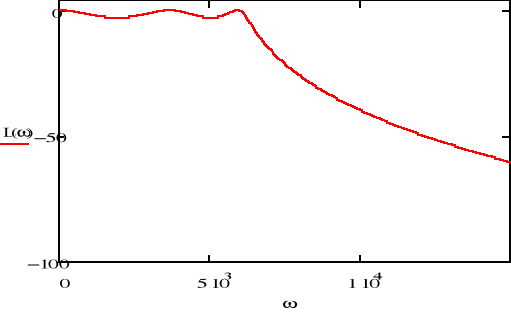
charakterystyka fazowa

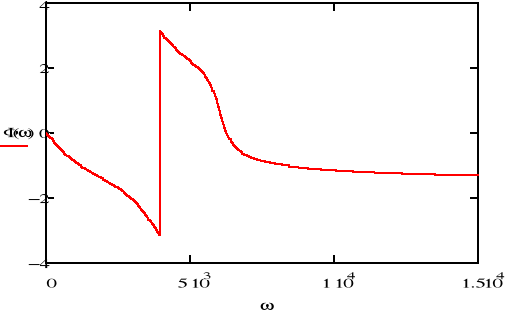
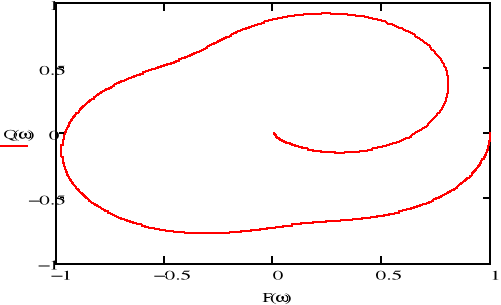
wykres Nyquista

Za pomocą funkcji invlaplace wyznaczamy odwrotna transformaty Laplace

Wyznaczenie charakterystyk czasowych

Odpowiedz impulsowa

Funkcja czasowa przyjmuje postać:

Odpowiedz impulsowa

Wyznaczenie czasu ustalania

Szacunkowy czas ustalania: ok.
s

Odpowiedź skokową wyznaczamy podobnie jak odpowiedź impulsowa z tym że przed przekształceniem mnożymy wyrażenie przez 1/s

Odpowiedz skokowa

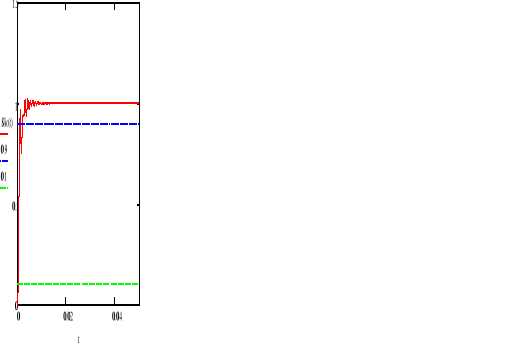
Szacunkowy czas narastania:
s

Opóźnienie grupowe

Obliczenie funkcji opóźnienia grupowego:

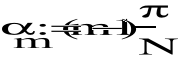
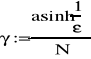
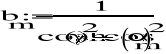
Wyznaczenie transmitancji filtru cyfrowego

Wyznaczanie transmitancji filtru cyfrowego odbywa się przez podstawienie za s

Transmitancja filtru cyfrowego przyjmuje postać:

Wyznaczenie charakterystyk częstotliwościowych

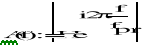
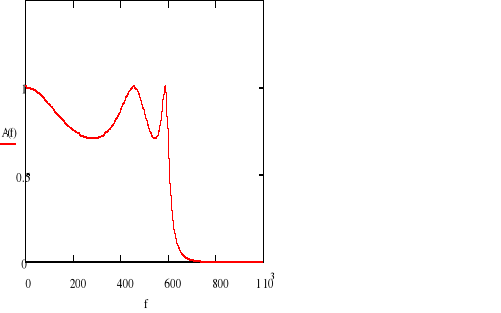
charakterystyka amplitudowa

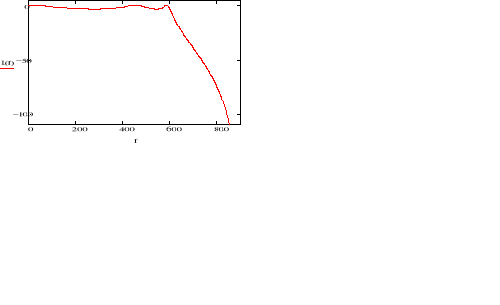
Charakterystyka amplitudowa logarytmiczna

Charakterystyka fazowa

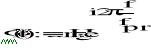
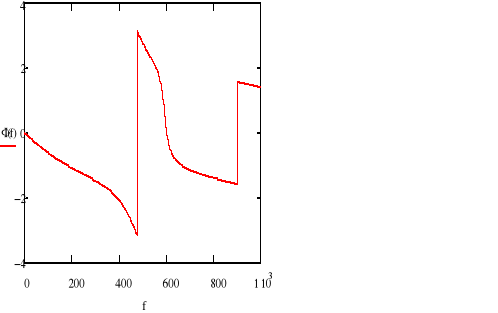
ANALIZA CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWEJ

Charakterystyka amplitudowa logarytmiczna

Na podstawie powyższej charakterystyki widać że maksymalne dopuszczalne tłumienie w paśmie przepustowym
jest równe zgodnie z założeniami 3dB, a częstotliwość końca pasma przepustowego równa 600Hz.

Na powyższej charakterystyce widać że filtr spełnia wytyczne w paśmie zaporowym, ponieważ charakterystyka przechodzi poniżej punktu

Na powyższej charakterystyce widać że dla przeprowadzonych obliczeń
, przy wymagalnym minimalnym tłumieniu w paśmie zaporowym
filtr spełnia założenia projektowe.

WPŁYW CZĘSTOTLIWOŚCI PRÓBKOWANIA NA UZYSKANE CHARAKTERYSTYKI

Przy zwiększeniu częstotliwości próbkowania zmienia się rząd filtru

Powyżej częstotliwości
rząd filtru zmienia się na 6

Powyżej częstotliwości
rząd filtru zmienia się na 7

Przy zmniejszeniu częstotliwości próbkowania rząd filtru maleje:

Poniżej częstotliwości
rząd filtru zmienia się na 4

Poniżej częstotliwości
rząd filtru zmienia się na 3

Wniosek: Aby filtr był rzędu 5 częstotliwość próbkowania powinna znajdować się w granicach od 1799 do 2147 Hz. Zwiększenia częstotliwości próbkowania poza ten zakres powoduje zwiększenie rzędu filtru. A zmniejszenie częstotliwości powoduje zmniejszenie rzędu filtru.

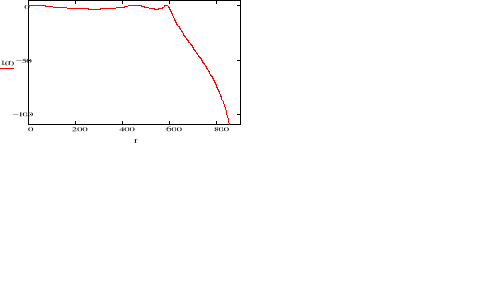
Zwiększenie częstotliwości próbkowania do

Charakterystyka amplitudowa logarytmiczna

Przy zwiększonej częstotliwości próbkowania o 200Hz zafalowania filtru są nadal na poziomie 3 dB

Jak widać w paśmie zaporowym charakterystyka zbliżyła się bardziej do punktu
, lecz znajdując się pod nim powoduje że filtr nadal spełnia założenia projektowe

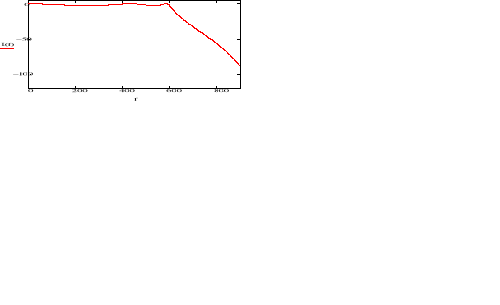
Zwiększenie częstotliwości próbkowania do

Charakterystyka amplitudowa logarytmiczna

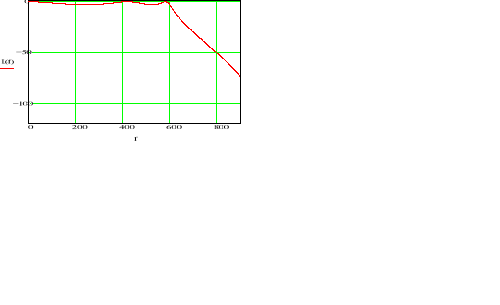
Przy zwiększonej częstotliwości próbkowania o 340Hz zafalowania filtru są nadal na poziomie 3 dB

Przy zwiększonej częstotliwości próbkowania do
jak widać na powyższej charakterystyce filtr znajduje się na granicy stabilności ponieważ wykres przechodzi przez punkt
. Dla częstotliwości próbkowania wyższych należy zwiększyć rząd filtru, aby filtr pracował optymalnie.

WNIOSKI

Projekt filtru dolnoprzepustowego Czebyszewa został wykonany w programie Mathcad.

Za pomocą tego programu w łatwy sposób można wykonywać różnego rodzaju obliczenia i wykresy. Część rzeczywista wszystkich biegunów transmitancji ma wartość ujemną, zapewnia to stabilność filtru. Rząd filtru zależy od częstotliwości próbkowania im większa częstotliwości próbkowania tym większy rząd, co za tym idzie filtr posiada lepsze właściwości, ale jego realizacja jest trudniejsza. Charakterystyk amplitudowa filtru cyfrowego jest funkcją okresową której okres wynosi 1/fp.

Charakterystyki czasowe informują nas o tym czy filtr jest stabilny czy nie. Badany filtr jest stabilny, jego odpowiedź impulsowa dąży do `0' i mamy do czynienia z gasnącymi oscylacjami. Odpowiedź na skok jednostkowy dąży do `1' gdyż, jak wiadomo, filtr dolnoprzepustowy przepuszcza składowe nisko częstotliwościowe i składową stałą, zaś tłumi składowe o wysokiej częstotliwości.

Rozważany przez nas filtr Czebyszewa typu I ma zafalowanie w paśmie przepustowym, za to nie ma zafalowań w paśmie zaporowym, ma mocno nieliniową charakterystykę fazową.

Na podstawie powyższych analizy charakterystyk można wywnioskować że filtr pracuje stabilnie i spełnia wymagania projektowe. Zgodnie z założeniami w paśmie przepustowym (0 - 600)Hz tłumienie filtru wynosi 3dB. Charakterystyka filtru przechodzi przez punkt
, dzięki czemu filtr pracuje prawidłowo. Na podstawie charakterystyk widać że filtr spełnia wytyczne w paśmie zaporowym, ponieważ charakterystyka przechodzi poniżej punktu
. Zmiany częstotliwości próbkowania mają wpływ na charakterystykę amplitudową filtru. Przy zwiększaniu częstotliwości próbkowania charakterystyka przechodzi coraz bliżej punktu
, jeżeli charakterystyka przejdzie nad tym punktem to filtr działa nieprawidłowo, charakterystyka musi przechodzić pod tym punktem. Zwiększanie częstotliwości próbkowania wpływa także na zmianę rzędu filtru. Zwiększanie częstotliwości próbkowania powoduje zwiększenie rzędu filtru, a zmniejszanie częstotliwości powoduje zmniejszanie rzędu. Na podstawie charakterystyk czasowych widać że filtr jest stabilny - widoczne są gasnące oscylacje zarówno w przebiegu odpowiedzi impulsowej i skokowej.

Na podstawie charakterystyki amplitudowej można stwierdzić że im bardziej stromo opada charakterystyka tym rząd filtru musi być większy. W przypadku obliczania rzędu filtru należy otrzymany wynik zaokrąglić do liczby całkowitej w górę. W naszym przypadku otrzymany wynik N:=4.005 został zaokrąglony w górę do N:=5, i właśnie dalsze rozwiązanie zadania opierały się na przyjętym piątym rzędzie filtru. Obliczona transmitancja filtru Czebyszewa nie ma zer, jej bieguny leża na elipsie o promieniu R (okrąg zewnętrzny) i r (okrąg zewnętrzny). Na podstawia obliczonych biegunów w łatwy sposób można obliczyć transmitancję filtru prototypowego, wiedząc że licznik jest iloczynem biegunów
, a mianownik iloczynem
. Po podstawieniu otrzymujemy transmitancję prototypowego filtru analogowego H(s). Aby przejść do transmitancji filtru analogowego należy dokonać transformację częstotliwości (transformata ta polega na podstawieniu za „s” odpowiedniej funkcji w wyniku czego otrzymujemy docelową transmitancję filtru analogowego). W przypadku naszego przekształcenia podstawiamy
. Po przeliczeniu otrzymujemy transmitancję filtru analogowego. Aby otrzymać transmitancję cyfrową należy zastosować transformację bilingową (dwuliniową) podstawiając
. Na podstawie otrzymanej transmitancji filtru cyfrowego otrzymujemy charakterystykę częstotliwościową amplitudową filtru, która jest najważniejszą częścią w sprawdzeniu poprawności pracy filtru.

W przypadku naszego filtru na podstawie charakterystyki stwierdzamy że filtr pracuje zgodnie z założeniami projektowymi.

BIBLIOGRAFIA:

1. Tomasz P. Zieliński: Cyfrowe przetwarzanie sygnałów. Od teorii do zastosowań. Wydawnictwa komunikacji i łączności, Warszawa 2005

2. Projektowanie filtrów cyfrowych Butterwortha i Czebyszewa http://teleinfo.pb.bialystok.pl/krashan/articles/filtry_iir/

3. Filtr Czebyszewa założenia teoretyczne i przykład projektowania. http://www.kmg.ps.pl/to/filtry_ak/czeby_p1.html

4. Filtry aktywne http://www.sppi.iit.pwr.wroc.pl/materialy/pliki/14-Filtry%20Aktywne.pdf

5. Mathcad instrukcja obsługi http://technologialaserowa.republika.pl/mathcad.pdf

6. Izydorczyk J., Płonka G., Tyma G.,: Teoria sygnałów, Helion Gliwice 1999

---