CEL ĆWICZENIA
Celem ćwiczenia jest zbadanie interferencji w doświadczeniu Younga.
PRZEBIEG POMIARU
Na ekranie umieszczamy kartkę papieru milimetrowego, a w uchwycie slajd z trzema szczelinami (jedną pojedynczą i dwiema podwójnymi), upewniając się, że wiązka lasera trafia dokładnie w szczelinki. Następnie z wielka starannością oznaczamy na papierze milimetrowym położenia minimów interferencyjnych. Pomiary powtarzamy dla dwóch pozostałych szczelinek, każdy notując na nowej kartce papieru milimetrowego.
WYNIKI POMIARÓW
x - kolejne maksima
y - odległość pomiędzy środkiem maksimum głównego a środkami kolejnych maksimów
DS 1
x |
y [cm] |
y [m] |
1 |
2,65 |
0,026 |
2 |
5,7 |
0,057 |
3 |
8,15 |
0,082 |
DS 2
x |
y[cm] |
y[m] |
1 |
1,35 |
0,0135 |
2 |
2,8 |
0,028 |
3 |
4,1 |
0,041 |
4 |
5,4 |
0,054 |
5 |
6,7 |
0,067 |
6 |
8,2 |
0,082 |
DS 3
x |
y[cm] |
y[m] |
1 |
0,4 |
0,004 |
2 |
1 |
0,01 |
3 |
1,35 |
0,0135 |
4 |
1,7 |
0,017 |
5 |
2,1 |
0,021 |
6 |
2,4 |
0,024 |
7 |
2,8 |
0,028 |
OBLICZENIA
Metodą najmniejszych kwadratów obliczamy współczynnik kierunkowy A oraz jego błąd pomiarowy ΔA, a następnie liczymy szerokość pomiędzy szczelinami oraz błąd tego pomiaru ze wzorów:
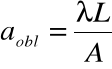
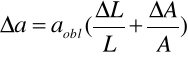
gdzie:
![]()
- to długość światła emitowanego przez laser i wynosi 635nm
L - odległość między ekranem a przeszkodą
A - współczynnik kierunkowy
![]()
- wynosi 0,003 m
DS 1
A= 2,8 *10-2(m)
ΔA= 0,17*10-2(m)
![]()
![]()
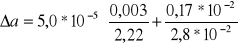
![]()
![]()
![]()
![]()
![]()
DS 2
A= 1,35 *10-2 (m)
ΔA= 0,029*10-2 (m)
![]()
![]()
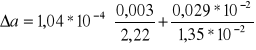
![]()
![]()
![]()
![]()
![]()
DS 3
A= 4,5 *10-3(m)
ΔA= 0,28*10-3(m)
![]()
![]()
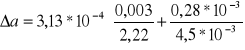
![]()
![]()
![]()
![]()
![]()
Wyniki
DS1 = 5,0*10-5 +/- 0,31*10-5
DS2 = 1,04*10-4 +/- 2,37*10-6
DS3 = 31,3*10-5 +/- 1,99*10-5
WNIOSKI
Po przeprowadzeniu badania można stwierdzić, że uzyskany przez nas obraz odpowiadam obrazowi z rysunku 2c. Jest to obraz uzyskany przez nałożenie dwóch efektów - interferencji i dyfrakcji. Na ekranie umieszczonym za przeszkodą uginającą światło obserwuje się powstanie obrazu w postaci ciemnych i jasnych prążków, które potwierdzają falową naturę światła. Ciemne paski to maksima, czyli miejsca, dla których energia nakładanych fal osiąga wartość największą; zaś jaśniejsze to minima, dla których energia nakładanych fal jest równa 0. Widoczność otrzymanego obrazu słabnie wraz ze wzrostem odległości od maksimum głównego, obraz staje się coraz bardziej niewyraźny.
1
![]()
![]()
![]()
![]()
![]()
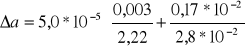
![]()
![]()
![]()
![]()
![]()
![]()
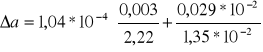
![]()
![]()
![]()
![]()
![]()
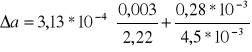
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Fizyka sprawozdanie moje, Laborki Fizyka Politechnika Łódzka, M6B,A
O3A7, Laborki Fizyka Politechnika Łódzka, O3A7
fizyka sprawozdanie m6 ab, Laborki Fizyka Politechnika Łódzka, M6B,A
tabeleNNN(1), Laborki Fizyka Politechnika Łódzka, W5
Laborki Fizyka, Laborki Fizyka Politechnika Łódzka, M6B,A
Cele ćwiczenia, Laborki Fizyka Politechnika Łódzka, M6B,A
Fizyka laborki wykresy, Laborki Fizyka Politechnika Łódzka, M6B,A
Ćwiczenie 4a, Laborki Fizyka Politechnika Łódzka
dane w3, Laborki Fizyka Politechnika Łódzka, W3A
tabeleNNN, Laborki Fizyka Politechnika Łódzka, W5
2, Laborki Fizyka Politechnika Łódzka, Fizyka wykłady- Wojciechowski
cel, Laborki Fizyka Politechnika Łódzka, T1
Pomiar promieniowania tła moje, Laborki Fizyka Politechnika Łódzka, W7
Sprawozdanie i konspekt 59 Dominika, Politechnika Łódzka Biotechnologia, Chemia fizyczna LABORKI
Sprawozdanie moje 44, BIOTECHNOLOGIA POLITECHNIKA ŁÓDZKA, CHEMIA FIZYCZNA
Sprawozdanie 55 ania, BIOTECHNOLOGIA POLITECHNIKA ŁÓDZKA, CHEMIA FIZYCZNA
gamma dobree!!, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
więcej podobnych podstron