Wykład Matematyka doc. Andrzej Drozdowicz

Pochodne

Różniczkowalność funkcji

Niech y=f(x) będzie funkcją określoną w pewnym otoczeniu punktu x₀

* Mówimy, że f(x) jest różniczkowalna w punkcie x₀ wtedy i tylko wtedy gdy istnieje taka stała A, że dla każdego przyrostu argumentu
gdzie o jest wielkością nieskończenie małą

Np.

Wtedy wyrażenie * przyjmuje postać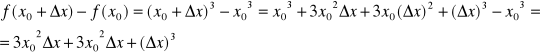

we wzorze * oznaczamy wzorem
i nazywamy różniczką funkcji f(x) w punkcie x₀ odpowiadającą przyrostowi argumentu x

Często oznacza się również

Z przykładu powyższego wynika, że dla f(x)=x³ różniczka tej funkcji w punkcie x₀ to

Natomiast w interpretacji geometrycznej:

• Funkcja y=f(x) jest różniczkowalna w punkcie x0 tylko wtedy, gdy ma w tym punkcie pochodną

• Jeżeli mamy do czynienia z funkcją większej ilości zmiennych np. 3 to mówimy wtedy o tzw różniczce zupełnej funkcji

Np.
wtedy wzór na różniczkę zupełną ma postać

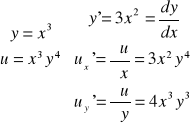
Różniczka funkcji znajduje zastosowanie w przypadku, gdy wielkości pochodzące z pomiarów nie są dokładne a podane są z pewnym błędem bezwzględnym wtedy błąd bezwzględny wielkości wyliczonej można wyznaczyć za pomocą różniczki zupełnej funkcji

Błąd bezwzględny

Błąd względny

Błąd względny %

Twierdzenie o pochodnej funkcji odwrotnej

Jeżeli funkcja różniczkowalna y=f(x) ma funkcję odwrotną
to pochodna tej funkcji to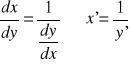

Przykład: dana jest funkcja y=tgx funkcja do niej odwrotna to x=arctgy

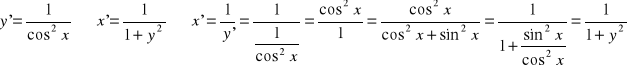
Mając na uwadze fakt, że pochodna funkcji złożonej jest równa iloczynowi pochodnej funkcji zewnętrznej i pochodnej funkcji wewnętrznej wzory 1-17 przyjmują postać

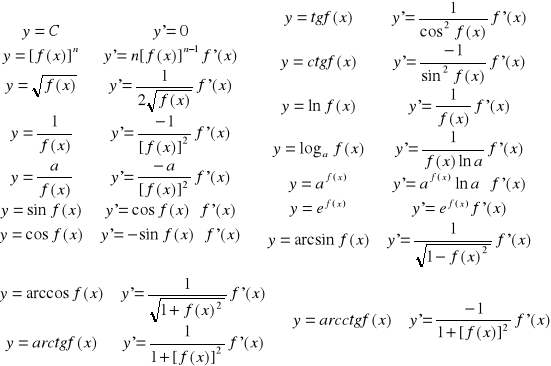
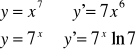
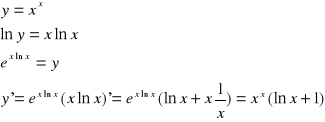
Jest to metoda pochodnej logarytmicznej

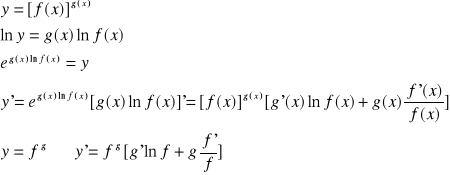
Przykład: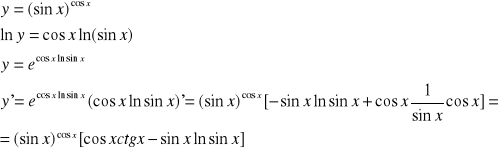

Matematyka wykład doc. Andrzej Drozdowicz 17.11.2009r.

---