Metalurgia

7 listopad 2005

ZESPÓŁ 5

Ćwiczenie nr. 6

Napięcie powierzchniowe w układzie faza ciekła- faza gazowa

Beata Olszewska

1. WSTĘP

Napięcie powierzchniowe to zjawisko fizyczne występujące na styku powierzchni cieczy z ciałem stałym, gazowym, lub inną cieczą. Polega na powstawaniu dodatkowych sił działających na powierzchnię cieczy w sposób kurczący ją (przyciągający do wnętrza cieczy). Zjawisko to ma swoje źródło w siłach przyciągania pomiędzy molekułami cieczy. Występuje ono także zawsze na granicy faz termodynamicznych.

Cząstka cieczy, znajdująca się na powierzchni fazowej ciecz-gaz, jest poddana oddziaływaniu sił między cząsteczkowych obydwu ośrodków. Siła wypadkowa, skierowana prostopadle do powierzchni fazowej, dąży, do wciągnięcia cząstki w głąb cieczy. Objawia się to dążnością układu do zmniejszenia powierzchni fazowej. Zjawisko to nazywa się napięciem powierzchniowym. Miarą napięcia powierzchniowego jest siła działająca na jednostkę długości na powierzchni fazowej ( siła styczna do tej powierzchni, dążąca do jej zmniejszenia) lub praca potrzebna do zwiększenia powierzchni fazowej o jednostkę. Równoważnymi wymiarami napięcia powierzchniowego są więc
oraz
( 10^-3N/m; 10^-3J/m).

Najmniejszą wartość stosunku wielkości powierzchni do objętością wykazuje kula. Stąd też, w wyniku działania napięcia powierzchniowego dążącego do zmniejszenia powierzchni fazowej, ciecze zawieszone w fazie gazowej przyjmują kształt kulistych kropel.

Tematem naszego ćwiczenia jest napięcie powierzchniowe na granicy faz ciekłej i fazy gazowej. Tak zwane napięcie powierzchniowe właściwe wyznacza się w układzie nie zawierającym obcych gazów (ciecz-para). Jednakże obecność obcych gazów, gdy nie reagują one z badaną cieczą, wpływa w zaniedbywalnie małym stopniu na mierzoną wielkość.

Zależność napięcia powierzchniowego cieczy od temperatury opisuje równanie Etövösa:

,

gdzie: M oznacza ciężar cząsteczkowy, d- ciężar właściwy (stąd
jest objętością jednego mola), T_K- temperatura krytyczna, K jest wartością stałą.

Zależność napięcia powierzchniowego od stężenia substancji rozpuszczonych posiada charakter złożony, zależny od rodzaju układu. Dla wodnych roztworów kwasów tłuszczowych zależność tę ujmuje równanie Szyszkowskiego:

gdzie: σ₀ oznacza napięcie powierzchniowe czystego rozpuszczalnika, σ- roztworu, a oraz b są stałymi, c - stężeniem.

Zależność napięcia powierzchniowego od stężenia wiąże się w tym przypadku ze zjawiskiem adsorpcji substancji rozpuszczonej na granicy fazowej. W przypadku stopów metali brak jest ogólnego równania ujmującego zależność napięcia powierzchniowego od stężenia. Dodatkowym czynnikiem komplikującym sytuację w tych układach jest możliwość powstawania różnych związków.

Jak wynika z definicji napięcia powierzchniowego, zmiana wielkości powierzchni fazowej wiąże się z efektami energetycznymi. Zmiana energii swobodnej związana ze wzrostem powierzchni o 1 cm² jest równa potrzebnej do tego pracy. Tak więc energia swobodna 1 cm² powierzchni fazowej jest równa napięciu powierzchniowemu:

.

Uwzględniając znane zależności

oraz

F = U - TS

można napisać

,

U oznacza tu całkowitą energię 1 cm² powierzchni fazowej.

2. METODY POMIAROWE

Istnieje szereg metod wyznaczania napięcia powierzchniowego na granicy faza ciekła- gazowa. W naszym ćwiczeniu wykorzystujemy dwie metody. A mianowicie metodę stalagmometryczną i pęcherzykową.

Metoda stalagmometryczna polega na pomiarze ilości kropel powstających podczas wypływu określonej objętości cieczy z rurki kapilarnej. Krople są tym większe (a więc tym mniej ich powstaje w danej objętości), im większe jest napięcie powierzchniowe.

rys. 1

rys. 2

Konstrukcję stalagmometru przedstawia rys. 2. Kropla cieczy u wylotu rurki kapilarnej znajduje się pod działaniem siły ciężkości oraz przeciwnie skierowanych sił napięcia powierzchniowego, działającego wokół zewnętrznego obwodu rurki o promieniu r. Oderwanie kropli następuje wówczas, gdy jej ciężar G zrównoważy siłę napięcia powierzchniowego, równą 2лrσ; w tym przypadku 2лr to obwód, na którego każdą jednostkę działa siła σ.

Na rys. 1 został przedstawiony wypływ kropli z kapilary. Linią przerywaną zaznaczono kolejne stadia formowania się kropli, linią ciągła natomiast kroplę w momencie odrywania się.

Licząc liczbę kropel powstających podczas wypływu tej samej objętości dwu różnych cieczy oraz znając ich ciężary właściwe, możemy wyliczyć stosunek ich napięć powierzchniowych.

,

gdzie: d oraz n oznaczają odpowiednio ciężary właściwe oraz liczbę kropel.

Metoda pęcherzykowa polega na pomiarze ciśnienia potrzebnego do wypchnięcia pęcherzyka gazu poprzez rurkę kapilarną, do badanej cieczy. Ciśnienie to mierzy się zazwyczaj układem manometrycznym pokazanym na rys. 3 (1- ciecz badana, 2- zbiornik z cieczą manometryczną).

rys. 3

Ze zbiornika 2 doprowadza się kroplami ciecz manometryczną aż do osiągnięcia ciśnienia powodującego wypchnięcie bańki gazu z kapilary. Mierząc to ciśnienie w przypadku dwu różnych cieczy oraz znajdując ich ciężary właściwe, możemy wyznaczyć stosunek napięć powierzchniowych tych cieczy:

,

gdzie: h' oznacza różnicę poziomów cieczy odczytaną na manometrze w momencie odrywania się bańki gazu, h- głębokość zanurzenia końca kapilary, d_m- ciężar właściwy cieczy manometrycznej, d₁ oraz d₂ to ciężary właściwe badanych cieczy.

3. CEL ĆWICZENIA

1. Pomiar napięcia powierzchniowego alkoholu oraz roztworu mydła metodami stalagnometryczną i pęcherzykową. Wyznaczenie błędów względnych i ocena dokładności metod.

2. Pomiar napięcia powierzchniowego (metodą stalagmometryczną lub pęcherzykową) roztworów wodnych mydła oraz alkoholu o różnych stężeniach. Ustalenie w oparciu o uzyskane wyniki zakresu stosowalności równania Szyszkowskiego oraz ewentualne wyznaczenie współczynników tego równania.

3. Wykreślenie na podstawie danych tabelarycznych zależności napięcia powierzchniowego wody, glinu, cynku, cyny, ołowiu i miedzi od temperatury. W oparciu o ten wykres należy wyznaczyć wartości
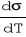
   . Należy również wyznaczyć całkowitą energię powierzchniową tych substancji.

4. WNIKI POMIAROWE

1. Wyniki pomiarów porównawczych napięcia powierzchniowego wykonanych metodą stalagmometryczną oraz pęcherzykową.

Substan -cja	Ilość kropel w kolejnych pomiarach (n)	Ciężar właściwy (d) [g/cm^3]		σX [dyn/cm]	Manometry-czna różnica poziomów (h') [mm]	Głębokość zanurzenia kapilary (h) [mm]		σX [dyn/cm]
H2O	48 49 47 średnio: 47	1,00	1,00	72,583	31 28 28 średnio: 29	21	1,00	72,583
alkohol 100%	143 150 144 średnio: 145,67	0,807	0,260	18,899	18 20 20 średnio: 19,33	21	0,298	21,620
roztwór detergentu [0,1%]	76 75 76 średnio: 75,67	1,00	0,621	45,083	27 28 28 średnio: 27,67	21	0,834	60,516

Przykład obliczeń dla alkoholu.

a) metoda stalagmometryczna

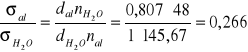
b) metoda pęcherzykowa

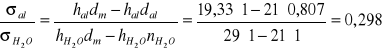
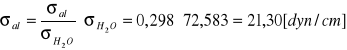
Błędy względne oznaczeń napięcia powierzchniowego:

Rzeczywisty ciężar właściwy wody: 0,9982[g/cm³]

Przyjęty w obliczeniach ciężar właściwy wody: 1[g/cm³]


=1-
=1- 0,9982=0,0018[g/cm³]≈ 0,002[g/cm³]

a) dla metody stalagmometrycznej:

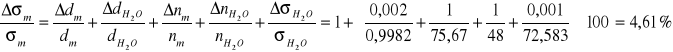
b) i pęcherzykowej:

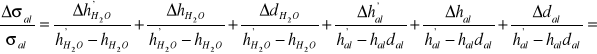
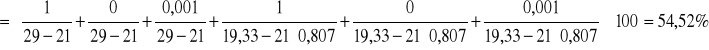
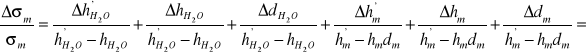
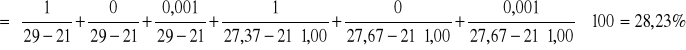
2. Wyniki pomiarów napięcia powierzchniowego roztworów wodnych alkoholu o różnych stężeniach.

Metoda stalagmometryczna:

Sporządzanie roztworów	Stę- żenie [%]	Ciężar właściwy dX [g/cm^3]	Ilość kropel nX [mm]	Napęcie powie-rzchniowe σ [dyn/cm]	Błąd wzgl. [%]
Roztwór wodny alkoholu metylowego	100	0,807	143 150 144 śr.:145,67	19,307	3,97	-0,193	-5,18
20ml roztw.100% + 5ml H2O	80	0,859	144 144 142 śr.: 143,33	20,904	3,98	-0,261	-3,83
25ml roztw.80% + 8,3ml H2O	60	0,909	142 140 141 śr.:141	22,501	3,99	-0,375	-2,67
33,3ml roztw.60% + 16,7ml H2O	40	0,948	136 136 136 śr.:136	24,315	4,02	-0,608	-1,65
20ml roztw.40% + 20ml H2O	20	0,974	102 103 102 śr.:102,33	33,170	4,26	-1,659	-0,60
20ml roztw.20% + 20ml H2O	10	0,985	80 74 79 śr.:77,67	44,203	4,57	-4,420	-0,23
20ml roztw.10% + 20ml H2O	5	0,991	64 64 64 śr.:64	53,947	4,85	-10,789	-0,09
10ml roztw.5% + 40ml H2O	1	0,997	54 58 60 śr.:57,33	60,607	5,03	-60,607	-0,02

Metoda pęcherzykowa:

Sporządzanie roztworów	Stę- żenie [%]	Ciężar właściwy dX [g/cm^3]	Ciśnienie mano-metryczne h'X [mm]	Głębokośc zanurzenia kapilary hX [mm]	Napęcie powie-rzchniowe σ [dyn/cm]	Błąd wzgl. [%]
Roztwór wodny alkoholu metylowego	100	0,807	18 20 20 śr.:19,33	21	21,630	54,52	-0,216	-4,62
20ml roztw.100% + 5ml H2O	80	0,859	15 20 20 śr.:18,33	21	2,64	356,50	-0,033	-30,30
25ml roztw.80% + 8,3ml H2O	60	0,909	20 20 20 śr.:20	21	8,265	122,39	-0,138	-7,26
33,3ml roztw.60% + 16,7ml H2O	40	0,948	22 22 22 śr.:22	21	18,980	60,36	-0,475	-2,11
20ml roztw.40% + 20ml H2O	20	0,974	23 33 21 śr.:25,67	21	47,324	31,70	-2,366	-0,42
20ml roztw.20% + 20ml H2O	10	0,985	27 23 27 śr.:25,67	21	45,228	32,59	-4,523	-0,22
20ml roztw.10% + 20ml H2O	5	0,991	27 25 25 śr.:25,67	21	44,085	33,11	-8,817	-0,11
10ml roztw.5% + 40ml H2O	1	0,997	26 25 25 śr.:25,67	21	42,942	33,66	-42,942	-0,02

3. Zależność napięcia powierzchniowego szeregu metali od temperatury.

H₂O:

Z wykresu σ=f(t^o) odczytuję równanie prostej y=ax+b

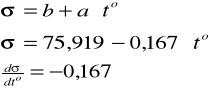
Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =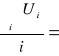
75,918

Sn

σ = -0,1988⋅t + 625,33

-0,1988

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =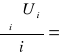
625,33

Pb

σ = -0,1658⋅t + 523,27

-0,1658

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =
523,27

Zn

σ = -0,1973⋅t + 858,03

-0,1973

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =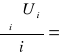
858,03

Al

σ = -0,141⋅t + 594,84

-0,141

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =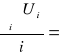
594,84

Cu

σ = -0,6066⋅t + 429,79

-0,6066

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =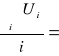
429,79

5. WNIOSKI

Na wykresie odwrotności pochodnej napięcia powierzchniowego od stężenia, przeprowadzonych dla obu metod pomiarowych (stalagmometrycznej i pęcherzykowej), układają się praktycznie na linii prostej dla stężenia alkoholu powyżej 40%.

Owe parametry prostej pozwoliły nam na wyliczenie stałych równania Szyszkowskiego. To równanie jest z dość dużą dokładnością spełnione dla obu metod pomiarowych.

Do naszych obliczeń możemy przyjmować, że gęstość wody wynosi 1g/cm³, ale tylko wtedy kiedy doświadczenie przeprowadzane jest w warunkach pokojowych. Różnica wartości rzeczywistej gęstości wody i naszej przyjętej jest bardzo mała, a co za tym idzie wynikający z tego błąd jest znikomy.

Punkty dla zależności napięć powierzchniowych metali od temperatury układają się mniej więcej wzdłuż linii prostych, z wyjątkiem Cu. Kąty nachylenia tych prostych pozwoliły nam na wyliczenie energii 1cm² powierzchni fazowej metali.

Z naszego ćwiczenia wynika, że metoda stalagmometryczna jest dokładniejsza od metody pęcherzykowej. Błędy względne pomiarów metodą stalagmometryczną wyniosły kilka procent. Natomiast metodą pęcherzykową zazwyczaj kilkadziesiąt.

Tak duży błąd dla tej metody wynika z tego, że odczyt różnicy poziomów cieczy manometrycznej odczytywaliśmy z dokładnością do 1mm, a to w stosunku do tego, że owa różnica wynosi od kilku do kilkunastu procent, dało nam duży błąd.

Ponadto łatwiej było nam policzyć ilość kropel wypływających z kapilary (nie myląc się), niż zaobserwować dokładny (idealny) moment wypłynięcia pęcherzyka (dokładnie jednego) z kapilary.

Błąd metody pęcherzykowej maleje, kiedy odczyt różnicy poziomów jest dokładniejszy, lub gdy różnica poziomów jest dużo większa. A także wtedy, kiedy cieczą wzorcową jest ciecz o dużym napięciu powierzchniowym.

Natomiast błąd pomiaru metodą stalagmometryczną maleje, gdy liczba wypływających kropel rośnie, oraz wtedy, kiedy cieczą wzorcową jest ciecz o małym napięciu powierzchniowym.

Wnioskując pomiar metodą stalagmometryczną jest dokładniejszy dla cieczy o małym napięciu powierzchniowym, co za tym idzie pomiar metodą pęcherzykową jest dokładniejszy dla cieczy o dużym napięciu powierzchniowym. Zauważyliśmy to wyraźnie dla zależności napięcia powierzchniowego od stężenia. Błąd pomiaru metodą stalagmometryczna jest mały na początku i stale rośnie, wraz ze wzrostem napięcia powierzchniowego cieczy badanej. Odwrotnie jest natomiast dla metody pęcherzykowej. Błąd pomiaru na początku jest bardzo duży i stopniowo maleje, wraz ze wzrostem napięcia powierzchniowego cieczy badanej.

---