POLITECHNIKA GDAŃSKA GDAŃSK 17.11.1999

KATEDRA MECHANIKI BUDOWLI

LABORATORIUM

ĆWICZENIE nr 11

WYZNACZENIE ŚRODKA ZGINANIA

WYKONALI:

Izabela Wicher

Renata Szczodrońska Aleksander Starczewski

SPRAWOZDANIE

1. OPIS POSZCZEGÓLNYCH DOŚWIADCZEN

Celem ćwiczenia jest wyznaczenie środka zginania (lub ścinania) dwóch cienkościennych belek wspornikowych : pierwszej - o przekroju pierścieniowym zamkniętym (doświadczenie 1) i drugiej - o przekroju pierścieniowym otwartym (doświadczenie 2).

Doświadczenia wykonujemy przy pomocy dwóch zestawów odpowiednio dla poszczególnych doświadczeń . W skład każdego zestawu wchodzi:

• belka,

• ruchoma szalka z odważnikami ,

• miarka umożliwiająca określenie położenia szalki,

• czujniki zegarowe umożliwiające pomiar przemieszczeń .

Przy pomocy odważników wywołujemy moment skręcający a na podstawie czujników dalej możemy wyznaczyć kąty przekrojów belek .

Doświadczenia rozpoczynamy i kończymy od pomiaru przemieszczeń na obu czujnikach przy nie obciążonym układu . Przy wyznaczeniu kąta obrotu uśredniamy odczyty początkowe z czujników w celu wyeliminowania błędu .Następnie obciążamy układ i dokonujemy pomiarów przemieszczeń w zależności od położenia ciężarka. Następnie wykonujemy wykres funkcji ugięć w zależności od obciążenia . Punkt w którym proste z poszczególnych czujników się przecinają jest szukanym środkiem zginania .

Doświadczenie 1:

Na jednym z końców pręta znajdowała się szalka zamocowana prostopadle do pręta. Ramię szalki posiadało wgłębienia co 5 cm w których to umieszczaliśmy siłę P=1kg ≈ 9,81 N.

Doświadczenie 2:

Na jednym z końców pręta znajdowała się szalka zamocowana prostopadle do pręta. Ramię szalki posiadało wgłębienia co 1 cm w których to umieszczaliśmy siłę P=1kg ≈ 9,81 N.

2.WYNIKI POMIARÓW

1. PRZEKRÓJ PIERŚCIENIOWY ZAMKNIĘTY

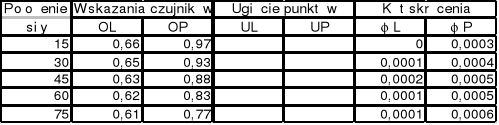
- Odczyty początkowe przy nieobciążonym układzie: OL₁ = 1,00 , OP₁ = 0,67

- Odczyty końcowe przy nieobciążonym układzie: OL₂ = 0,99 , OP₂ = 0,66

- Średnie odczyty początkowe: OL = 0,5( OL₁ + OL₂ ) = 0,5 (1,00+0,99) = 0,995 ≈1,00

OP = 0,5( OP₁ + OP₂) = 0,5 (0,67+0,66) = 0,665 ≈0,66

- Kąt skręcenia na podstawie otrzymanych wyników: (u_l+u_p)/a

2.2 PRZEKRÓJ PIERŚCIENIOWY OTWARTY

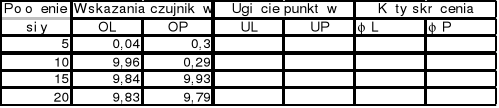
- Odczyty początkowe przy nieobciążonym układzie: OL₁ = 0,75 , OP₁ = 2,01

- Odczyty końcowe przy nieobciążonym układzie: OL₂ = 0,74 , OP₂ = 2,01

- Średnie odczyty początkowe: OL = 0,5( OL₁ + OL₂ ) = 0,5 (1,00+0,99) = 0,995 ≈1,00

OP = 0,5( OP₁ + OP₂) = 0,5 (2,01 +2,01) = 2,01

• Kąt skręcenia na podstawie otrzymanych wyników: (u_l+u_p)/a

3. OBLICZENIA TEORETYCZNE

1. PRZEKRÓJ PIERŚCIENIOWY ZAMKNIĘTY

R=3,92 cm

dA=dSδ dS=Rdϕ

dA=Rδdϕ

y=Rcosϕ

Środek zginania- punkt w którym należy przyłożyć siłę aby zredukować wypadkową naprężeń stycznych ( siła w tym punkcie nie wywołuje skręcania ) .

czyli:

∑ MsO=0 , stąd :

T x - ∫ dt R = 0

T x - t R = 0 (1) t-wypadkowa naprężeń stycznych

τ = (Sx T)/(Ix δ) Ix-moment bezwładności przekroju:

Ix = 0,5 Π R³δ

Sx-moment statyczny:

Sx = ∫ y dA

Sx = ∫ R cosϕ R δ dϕ = ∫ R² δ cosϕ dϕ = R² δ cosϕ + c

Wiedząc , że dla: Sx (ϕ = 0) = 0 , stała c = 0 .

Sx = R² δ sinϕ .

τ = (R² δ sinϕ T)/( 0,5 Π R³δ δ) = ( 2 sinϕ T)/(R δ Π )

t = ∫ τ dA = ∫ (( 2 sinϕ T )/( R δ Π )) R δ dϕ = ( 2 T ) / Π [ - cosϕ ] = ( 2 T ) / Π [ - ( -1-1)] = 4 T / Π .

Podstawiając do równania (1) , otrzymujemy :

T x = (4 T / Π) R

x = ( 4/Π ) R = 4 (3,92/Π) = 4,99 cm

Zgodnie z przyjętym układem współrzędnych w doświadczeniu odległość od punktu zginania równa się :

e = 4,50 - 4,99 = - 0,49 cm .

3.2 PRZEKRÓJ PIERŚCIENIOWY OTWARTY

Korzystam z warunku jak w 3.1:

∑ MsO=0 , stąd :

Ty x - T₁ a - T₂ a = 0

∑X = 0 , stąd :

T₁ = T₂

∑Y = 0 , stąd :

Ty = T₁ + T₂

podstawiając do równania (1)

(T₁ + T₂ ) x = (T₁ + T₂ ) a

x = a

Wiedząc , że a = 5,3 cm otrzymujemy : x = 5,3 cm .

Zgodnie z przyjętym układem wsp. w doświadczeniu odległość od punktu zginania równa się :

e = 5,50 - 5,30 = 0,20 cm.

4.PORÓWNANIE WYNIKÓW DOŚWIADCZEŃ Z OBLICZENIAMI TEORETYCZNYMI

RODZJ PRZEKROJU	WARTOŚĆ DOŚWIADCZALNA	WARTOŚĆ TEORETYCZNA
RUROWY	-7,5	-4,9
KĄTOWY	1,35	2,0

5.OBLICZANIE POŁOŻENIA ŚRODKA CIĘŻKOŚCI PRZEKROJU POPRZECZNEGO BELKI .

1. PRZEKRÓJ RUROWY

R = 3,92 cm .

x = R sinϕ

A = ∫ R δ dϕ = R Π δ

Środek ciężkości S (Xc , Yc) . Xc = Sy/A Yc = Sx/A

Yc = 0 ,ponieważ moment statyczny wzgl. osi X = 0 - przekrój monosymetryczny .

Xc = Sy/A

Sy = ∫ x dA

Sy = ∫ R sinϕ R δ dϕ

Sy = -R² δ cosϕ = -R² δ ( -1-1) = 2 R² δ

Xc = ( 2 R² δ )/( 2 Π δ ) = 2 R / Π = 2,496 cm .

Zgodnie z przyjętym układem współrzędnych w doświadczeniu Xc = 4,50 - 2,496 = 2,004cm .

2. PRZEKRÓJ KĄTOWY.

x = 2,65 cm .

A = 2 δ 7,5 = 5,25 cm² .

Środek ciężkości S (Xc , Yc) . Xc = Sy/A Yc = Sx/A

Yc = 0 ,ponieważ moment statyczny wzgl. osi X = 0 - przekrój monosymetryczny .

Xc = Sy/A

Sy = A x

Sy = 5,25 ∗ 2,65 = 13,91 cm³ .

Xc = 13,91/5,25 = 2,65 cm .

Zgodnie z przyjętym układem współrzędnych w doświadczeniu Xc = 5,50 - 2,65 = 2,85cm .

6. POMIAR KĄTA SKRĘCANIA DLA PRZYPADKU OBCIĄŻENIA SIŁĄ PRZYŁĄŻONĄ W ŚRODKU CIĘŻKOŚCI PRZEKROJU POPRZECZNEGO .

1. PRZEKRRÓJ RUROWY

U_l =

U_p =

ϕ = ( U_l - U_p )/a =

2. PRZEKRÓJ KĄTOWY

U_l =

U_p =

ϕ = ( U_l - U_p )/a =

7.UWAGI WŁASNE

W wykonywanym ćwiczeniu zarówno w doświadczeniu nr1 jak i w doświadczeniu nr2 , wyznaczaliśmy środki zginania , czyli punkty w których należy przyłożyć siłę tnącą aby nie wywołała momentu skręcającego .Studiując wykresy funkcji ugięć w zależności od obciążenia znajdujemy punkt przecięcia się dwóch wykresów - jest to punkt w którym nie występuje skręcenie czyli nasz szukany punkt .

Położenie punktu wyznaczone doświadczalnie i teoretycznie różni się nieznacznie zarówno przy przekroju rurowym jak i kątowym . Różnicę tę upatrujemy:

- w niedokładności pomiarów - wiąże się to z niedokładnością przyrządów oraz błędnego

odczytania z czujników pomiarowych .

- niedokładnego naniesienia punktowo wykresu potrzebnego do określenia środka zginania

- niedokładnego odczytu położenia środka zginania z w.w. wykresu .

5

2

---