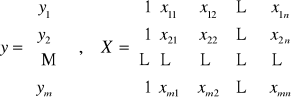
Wykład 1

Termin ekonometria używany jest w polskiej literaturze w dwóch znaczeniach. W szerszym znaczeniu jako zespół metod matematycznych i statystycznych stosowanych do badań ekonomicznych. W węższym znaczeniu oznacza specyficzne metody statystyczne stosowane w badaniach nieeksperymentalnych.

Ekonometria zajmuje się badaniem - mierzeniem danych ekonomicznych, badaniem obserwacji empirycznych za pomocą statystycznych metod estymacji i testowania hipotez.

Badania empiryczne i teoretyczne wzajemnie się uzupełniają. Analizy teoretyczne poddawane są weryfikacji przy pomocy danych empirycznych. Z drugiej strony do badań statystycznych potrzebne są wskazówki płynące z teorii ekonomicznych.

Podstawowym obiektem rozpatrywanym w ekonometrii jest model ekonometryczny czyli formalny zapis procesu lub zjawiska ekonomicznego. Tym formalnym zapisem jest równanie lub zespół równań wiążących rozważane zmienne.

Równanie zbudowane jest: ze zmiennych objaśnianych, objaśniających o ustalonej treści ekonomicznej; parametrów strukturalnych; składniku losowym o nieustalonej treści ekonomicznej; związku funkcyjnego łączącego te wszystkie wielkości.

Zmienna to coś co może się zmieniać, przyjmować różne wartości. Zmienne często występujące w rozważaniach ekonomicznych to: praca, zysk, koszt, dochód narodowy, import, export…

Klasyfikacja zmiennych występujących w modelu ekonometrycznym.

1. Ze względu na źródło zmienności:

1. Zmienne endogeniczne (bieżące i opóźnione, generowane od wewnątrz), zmienne określane (wyjaśniane) na podstawie modelu;

2. Zmienne egzogeniczne (bieżące i opóźnione, generowane z zewnątrz), wartości tych zmiennych są dane, ustalone. Zmienne nie wyjaśniane przez model.

2. Ze względu na rolę pełnioną przez zmienne w modelu:

1. Zmienne objaśniane;

2. Zmienne objaśniające.

Klasyfikacja modeli ekonometrycznych

1. Ze względu na liczbę równań

1. Modele jednorównaniowe

2. Modele wielorównaniowe

2. Ze względu na postać analityczną równań

1. Modele liniowe

2. Modele nieliniowe sprowadzalne do postaci liniowej - takie, które po przekształceniu przybierają postać liniową:

3. Modele nieliniowe i niesprowadzalne do postaci liniowej

3. Ze względu na rolę odgrywaną przez czas

1. Modele statyczne - prezentujące dane przekrojowe, dane z jednego okresu czasu

2. Modele dynamiczne - prezentujące zjawisko w czasie, szeregi czasowe

1. Model trendu

2. Model autoregresyjny

4. Ze względu na poznawcze cechy modelu.

1. Modele przyczynowo-skutkowe

2. Modele symptomatyczne

3. Modele trendu

5. Według charakteru powiązań między zmiennymi

1. Modele proste

2. Modele rekurencyjne

3. Modele o równaniach współzależnych.

6. Jeżeli za punkt odniesienia przyjmiemy cel budowy modelu to możemy wyróżnić:

1. Modele opisowe - budowane w celach poznawczych, głównie do celów opisowych bądź weryfikacji stawianych hipotez ekonomicznych;

2. Modele optymalizacyjne - klasyczne zagadnienie optymalizacji produkcji, zagadnienie diety;

3. Modele bilansowe - zagadnienia nakładów i wyników produkcji.

7. Możemy klasyfikować modele ze względu na występowanie w modelu wielkości losowej:

1. Modele deterministyczne - modele optymalizacyjne, modele bilansowe;

2. Modele stochastyczne - modele opisowe zjawisk gospodarczych.

8. Często stosuje się też podział modeli ze względu na zjawiska opisywane zmiennymi objaśnianymi:

1. Modele makroekonomiczne;

2. Modele mikroekonomiczne;

3. Branżowe

4. Regionalne

5. Gospodarki narodowej;

6. Handlu zagranicznego, itp…

Proces budowy modelu ekonometrycznego.

W pierwszym etapie ustalana jest mierzalna zmienna endogeniczna Y (objaśniana). Na podstawie uznawanej teorii ekonomicznej lub na podstawie zebranego materiału empirycznego formułuje się hipotezę, co do postaci modelu, zbioru zmiennych objaśniających X={X₁, X₂,… X_m} i zależności między zmiennymi występującymi w modelu. Tak, więc model matematyczny badanego zjawiska, czyli równanie lub układ równań wiążących rozważane przez nas zmienne są wynikiem merytorycznej analizy rozważanego zjawiska.

Zmienne mierzalne, niemierzalne, dostępne, niedostępne. Dane statystyczne: szereg czasowy, dane przekrojowe.

Przy braku teorii ekonomicznej wybieramy jako zmienne objaśniające te, które są silnie skorelowane ze zmienną objaśnianą i słabo skorelowane między sobą oraz mają związek ekonomiczny ze zmienną objaśnianą.

Y = f (X₁, X₂,… X_n, )

W drugim etapie zbieramy dane empiryczne, na podstawie których będziemy chcieli wyznaczyć parametry modelu i estymujemy wartości parametrów modelu.

W trzecim etapie weryfikujemy poprawność naszego modelu na podstawie nowych danych empirycznych.

W czwartym etapie stosujemy zbudowany i zweryfikowany model do celów do jakich był budowany.

Zweryfikowany model może być wykorzystywany do:

1. Badania ilościowych związków między badanymi zmiennymi objaśnianymi, a zmiennymi objaśniającymi;

2. Do prognoz;

3. Do poszukiwania optymalnych decyzji, itp. …

Dobór zmiennych objaśniających w modelu liniowym

Y = ₀ + ₁X₁ + ₂X₂ + … + _nX_n + 

Chcemy by zmienne objaśniające miały następujące własności:

1. miały wystarczająco dużą zmienność;

2. były silnie skorelowane ze zmienną objaśnianą;

3. były słabo skorelowane między sobą;

4. były silnie skorelowane ze zmiennymi nie występującymi w modelu, które reprezentują.

Niech y będzie wektorem obserwacji zmiennej objaśnianej, X rozszerzoną macierzą obserwacji zmiennych objaśniających X₁, X₂,… X_n . Dokonano m obserwacji:

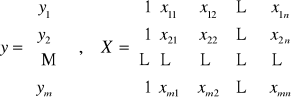
Eliminowanie zmiennych quasi-stałych

Miarą poziomu zmienności zmiennej jest następujący współczynnik zmienności:

gdzie

średnia arytmetyczna zmiennej X_i

odchylenie standardowe zmiennej X_t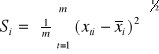

Ustalana jest pewna wartość krytyczna ^*. Jeśli v_i ≤ v^* to uznajemy zmienną za quasi-stałą i eliminujemy ze zbioru potencjalnych zmiennych objaśniających.

Przykład 1

Budujemy liniowy model ekonometryczny. Jako wartość krytyczną dla współczynnika zmienności przyjmujemy v^* = 0,15.

Rok	Y	X1	X2	X3	X4
1993	12	6	11	5	35
1994	12	8	14	4	35
1995	15	10	15	5	38
1996	14	10	16	5	40
1997	16	8	18	4	41
1998	18	10	20	8	42
1999	17	12	19	6	42
2000	19	10	20	8	43
2001	20	12	15	7	44
2002	20	14	22	8	40
X^śri	E(X)	10,0	17,0	6,0	40,0
Si	S(X)	2,19	3,19	1,55	2,97
i	v(X)	0,22	0,19	0,26	0,07

Zmienna X₄ jako quasi-stała musi być odrzucona.

Obliczenia do przykładu 1:

	X4	X4-X^śr4	(X4-X^śr4)^2
	35	-5	25
	35	-5	25
	38	-2	4
	40	0	0
	41	1	1
	42	2	4
	42	2	4
	43	3	9
	44	4	16
	40	0	0
suma	400		88
X^śr4	40		8,8	Var(X4)
			2,97	S4

Wektor i macierz współczynników korelacji

Ocenę siły liniowej zależności między zmienną objaśnianą Y a zmiennymi objaśniającymi X_i dokonujemy przy pomocy współczynnika korelacji r_i :

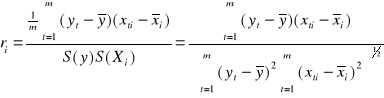
Ocenę siły liniowej zależności między zmiennymi objaśniającymi X_i X_j dokonujemy przy pomocy współczynnika korelacji r_ij :

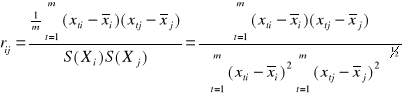
Współczynniki te przedstawiamy odpowiednio w postaci wektora i macierzy :

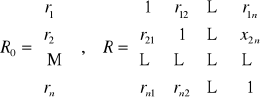
Przykład 2 (cd przykładu 1)

Obliczmy r₄:

	Y	X4	Y-Y^śr	X4-X^śr4	(Y-Y^śr)(X4-X^śr4)	(Y-Y^śr)^2	(X4-X^śr4)^2
	12	35	-4,3	-5	21,5	18,49	25
	12	35	-4,3	-5	21,5	18,49	25
	15	38	-1,3	-2	2,6	1,69	4
	14	40	-2,3	0	0	5,29	0
	16	41	-0,3	1	-0,3	0,09	1
	18	42	1,7	2	3,4	2,89	4
	17	42	0,7	2	1,4	0,49	4
	19	43	2,7	3	8,1	7,29	9
	20	44	3,7	4	14,8	13,69	16
	20	40	3,7	0	0	13,69	0
suma	163	400			73	82,1	88
średnia	16,3	40					7224,8	iloczyn
				r4	0,86		85,00	pierwiastek

Obliczmy r₁₄ :

	X1	X4	X1-X^śr1	X4-X^śr4	(X1-X^śr1)(X4-X^śr4)	(X1-X^śr1)^2	(X4-X^śr4)^2
	6	35	-4	-5	20	16	25
	8	35	-2	-5	10	4	25
	10	38	0	-2	0	0	4
	10	40	0	0	0	0	0
	8	41	-2	1	-2	4	1
	10	42	0	2	0	0	4
	12	42	2	2	4	4	4
	10	43	0	3	0	0	9
	12	44	2	4	8	4	16
	14	40	4	0	0	16	0
suma	100	400			40	48	88
średnia	10	40			pierwiastek	6,93	9,38
						iloczyn	64,99
						r14	0,62

Metoda analizy współczynników korelacji

W tej metodzie wybieramy zmienne objaśniające silnie skorelowane z ze zmienną objaśnianą, a słabo skorelowane między sobą. Do analizy używamy wektora R₀ i macierzy R.

Dla danego poziomu istotności γ oraz (m-2) stopni swobody, gdzie m to ilość obserwacji wyznacza się krytyczną wartość współczynnika korelacji r^* :

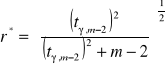
Ekonometra może sam arbitralnie ustalić wartość krytyczną r^*.

Procedura ustalania zmiennych objaśniających wygląda następująco:

1. Ze zbioru potencjalnych zmiennych objaśniających usuwa się wszystkie dla których | r_i | ≤ r^* uznając, że są za mało skorelowane ze zmienną objaśnianą

2. Z pozostałych zmiennych wybranych do objaśniania wybieramy X_i tą, która ma największą korelację ze zmienną objaśnianą | r_i | = max { |r_k| ; k = 1, 2,… m}

3. Eliminujemy teraz wszystkie zmienne X_j, które są zbyt mocno skorelowane z wybraną zmienną X_i , tzn te dla których zachodzi |r_ij| > r^* .

Postępowanie opisane w punktach 1, 2, 3 powtarzamy aż do wyczerpania wszystkich potencjalnych zmiennych objaśniających.

Przykład 4 (Nowak str 19)

Chcemy wyjaśnić wielkość spożycia mięsa przy pomocy z spożycia innych produktów:

Y - spożycie mięsa - zmienna objaśniana

X₁ - artykuły zbożowe, X₂ - ziemniaki, X₃ - warzywa, X₄ - owoce, X₅ - tłuszcze, X₆ - ryby, X₇ - mleko, X₈ - jajka.

Na podstawie danych statystycznych z 28 krajów obliczono odpowiednie korelacje:

	-0,59			1	-0,09	0,35	-0,17	-0,26	-0,40	-0,16	-0,55
	-0,06			-0,09	1	-0,06	-0,38	0,00	0,15	0,22	0,11
	0,08			0,35	-0,06	1	0,33	-0,11	-0,20	-0,45	-0,02
R0 =	0,13		R =	-0,17	-0,38	0,33	1	0,20	-0,07	-0,44	0,07
	0,54			-0,26	0,00	-0,11	0,20	1	0,22	0,17	-0,11
	-0,15			-0,40	0,15	-0,20	-0,07	0,22	1	-0,19	0,47
	-0,10			-0,16	0,22	-0,45	-0,44	0,17	-0,19	1	0,05
	0,72			-0,55	0,11	-0,02	0,07	-0,11	0,47	0,05	1

Z tablic testu t-Studenta dla poziomu istotności γ = 0,10 oraz dla (m-2) = 26 stopni swobody odczytujemy wartość krytyczną t_{0,1 ; 26} = 1,706.

Następnie obliczamy wartość krytyczną współczynnika korelacji:

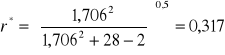
Eliminujemy najpierw wszystkie zmienne zbyt słabo skorelowane ze zmienną objaśnianą, czyli zmienne X₂, X₃, X₄, X₆, X₇.

Z pozostałych wybieramy pierwszą zmienną objaśniającą czyli najsilniej skorelowaną ze zmienną objaśnianą. Wybieramy X₈.

Eliminujemy teraz zmienne X zbyt silnie skorelowane ze zmienną X₈ czyli spełniające |r_8j|>0,317. Wyeliminowana zostaje X₁. Jako druga zmienna objaśniająca zostaje przyjęta X₅.

Ostatecznie przyjmujemy dwie zmienne objaśniające: X₅, X₈.

Y = ₀ + ₁X₅ + ₂X₈ +  .

Dobór zmiennych objaśniających (metoda Helwiga)

Ilość zmiennych objaśniających nie może być zbyt duża. Musimy mieć kryterium według którego będziemy je wybierać.

Przypuśćmy, że zmienne X₁, X₂, … X_n są kandydatkami na zmienne objaśniające. Wybierzemy te zmienne, które mają największą pojemność informacyjną.

Niech r_ij oznacza współczynnik korelacji liniowej Perasona między zmiennymi X_i , X_j ; r_j zaś między X_j , Y.

Niech S oznacza podzbiór zbioru {1, 2, … n}

Oznaczenie

- indywidualna pojemność informacyjna nośnika X_j , j należy do S:

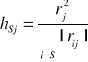
- integralna pojemność informacyjna podzbioru S:

Przykład 3

Dla zmiennej objaśnianej Y wybrano dwie zmienne objaśniające X₁, X₂ .

Wyliczone zostały dla nich macierze współczynników korelacji:

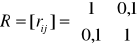
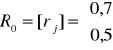
Wybrać optymalny w sensie Hellwiga zbiór zmiennych objaśniających.

H₁ = h₁₁ = 0,49 = (0,7)²/ 1 ;

H₂ = h₂₂ = 0,25 = (0,5)²/ 1 ;

h_{1,2}1 = ( 0,49 ) / (1 + 0,1 ) = 0,445

h_{1,2}2 = ( 0,25 ) / (1 + 0,1 ) = 0,227

H_{1,2} = h_{1,2}1 + h_{1,2}2 = 0,672

W rozważanym przypadku optymalnym w sensie Hellwiga jest zbiór { X₁ , X₂ } jako zbiór objaśniający.

Wykład 2

Nieliniowe modele ekonometryczne

W ekonometrii często wykorzystujemy modele liniowe gdyż:

• mają prostą interpretację ekonomiczną

• są łatwe w estymacji

• łatwa jest ich statystyczna weryfikacja

• często są wystarczająco dobrym przybliżeniem rzeczywistości ekonomicznej

• wiele modeli nieliniowych daje się sprowadzić do postaci liniowej (linearyzować).

Najprostszym przykładem jest model liniowy jednorównaniowy:

Y = a₀ + a₁X₁ + a₂X₂ + … + a_nX_n +  (1)

gdzie: Y - zmienna objaśniania,

X­_i ­- zmienne objaśniające, i = 1, 2, … n

a_i - nieznane parametry strukturalne modelu, i = 0, 1, … n

 - składnik losowy.

Naszym celem jest oszacowanie parametrów modelu a_i , i = 0, 1, … n.

W równaniu (1) zarówno zmienne objaśniające X­_i ­jak i parametry strukturalne a_i , pojawiają się w sposób liniowy. Jeśli model opisujący zależność między zmienną objaśnianą i zmiennymi objaśniającymi nie jest postaci (1), to jest to model nieliniowy, trudniejszy do analizy. Ponieważ jednak naszym celem jest oszacowanie parametrów strukturalnych, więc uznamy, ze model jest prosty jeśli będzie liniowy ze względu na parametry (nie musi być liniowy ze względu na zmienne). W dalszych rozważaniach będziemy klasyfikowali modele na liniowe ze względu na parametry strukturalne i nieliniowe ze względu na te parametry.

Przykład 1.

1. Y = a + bX + cZ +  ; model liniowy ze względu na parametry i zmienne,

2. Y = a + bX + cX² +  ; model liniowy ze względu na parametry i nieliniowy ze względu na zmienne,

3. Y = a + bX + b²Z +  ; model nieliniowy ze względu na parametry i liniowy ze względu na zmienne,

4. Y² = a + bX + b²X² +  ; model nieliniowy ze względu na parametry i zmienne.

Ogólna postać modelu liniowego ze względu na parametry ma postać:

g(Y) = a₀ + a₁f₁(X) + a₂f₂(X) + … + a_nf_n(X) +  (2)

gdzie: Y - zmienna objaśniania,

X = (X­₁, X­₂,… X­_n) ­- wektor zmiennych objaśniających

a_i - nieznane parametry strukturalne modelu, i = 0, 1, … n

 - składnik losowy.

Jeśli g(Y) = Y, to mówimy, że (2) jest modelem bezpośrednio liniowym. Jeśli g jest funkcja odwracalną to (2) jest linearyzcją (sprowadzeniem do postaci liniowej) modelu (2a).

Y = g^-1{a₀ + a₁f₁(X) + a₂f₂(X) + … + a_nf_n(X) +  (2a)

Model (2a) nazwiemy modelem linearyzowanym.

Przykład 2.

Badamy model (wykładniczo hiperboliczny) postaci:

; gdzie d, h > 0 (3a)

Model (3a) jest modelem linearyzowalnym. Logarytmując obustronnie równanie (3a) przechodzimy do modelu (3b) postaci:

ln (Y) = ln(d) + b/X + ln(h) (3b)

Przyjmując oznaczenia: a = ln(d),  = ln(h) sprowadzamy równanie (3b) do postaci liniowej ze względu na parametry:

ln(Y) = a + b/X +  (

Używając metody wyznaczania parametrów w modelu liniowym, możemy obliczyć â estymator parametru a. Powstaje jednak pytanie czy exp(â) jest dobrym estymatorem parametru d. Przy odpowiednich założeniach (klasycznych założeniach stochastycznych) exp(â) jest zgodnym estymatorem parametru d. Jest to jednak estymator obciążony.

Jak widać na podstawie przykładu 2, możemy wyznaczać parametry strukturalne modelu linearyzowanego. Podobnie możemy postępować w ogólnym przypadku równania (2). Zagadnienie wyznaczania oryginalnych parametrów modelu przed linearyzacją, na podstawie estymatorów a_i parametrów modelu linearyzowanego, nazywamy zagadnieniem identyfikacji parametrów oryginalnych.

Model liniowy czy nieliniowy? Jaki model powinniśmy zastosować dla opisu badanego zjawiska, zbioru zaobserwowanych danych? Nie istnieją jednolite reguły postępowania. Musimy posłużyć naszą wiedzą ekonomiczną, doświadczeniem związanym z budową modeli ekonometrycznych, testami statystycznymi.

Przyrost krańcowy i elastyczność.

Przyrost krańcowy zmiennej objaśnianej Y względem zmiennej objaśniającej X_i to pochodna cząstkowa:

Przyrost krańcowy interpretujemy jako proporcję: przyrostu wielkości Y do przyrostu wielkości X_i, przy małym przyroście X_i i niezmienionych pozostałych wielkościach zmiennych objaśnianych. W przypadku, gdy przyrost krańcowy jest stałą niezależną od wszystkich zmiennych objaśniających to zmienna X_i w modelu pojawia się w sposób liniowy, zaś współczynnik przy X_i jest równy przyrostowi krańcowemu. Jeśli przyrost krańcowy nie jest wielkością stałą, to X_i w modelu występuje w sposób nieliniowy.

Elastyczność cząstkowa jest również miarą określającą zmienność zmiennej objaśnianej w zależności od zmienności zmiennej objaśniającej X_i. Elastyczność to iloczyn przyrostu krańcowego i proporcji X_i do Y:

W modelu liniowym E_Y|Xi = a_i · (X_i / Y).

Przykład 3

Model potęgowy: Y = a · X^b · 

Linearyzujemy logarytmując obie strony równania: ln(Y) = ln(a) + b·ln(X) + ln()

Wartość krańcowa dla modelu potęgowego wynosi: a · b · X^b-1 · 

Elastyczność Y względem X wynosi: b

Przykład 4

Rozważmy model postaci: Y = a + b·ln(X) +  , przy założeniu , że X>0.

Wartość krańcową Y względem X: dY/dX = b/X

Obliczmy elastyczność Y względem X: dY/dX · X/Y = b/X · X/Y = b/Y

Typowe modele liniowe ze względu na parametry - przykłady

W modelach liniowych ze względy na parametry, szacowanie parametrów weryfikacja modeli i prognozowanie dokonywana jest tak jak w modelach liniowych przy odpowiednim przedefiniowaniu zmiennych. Zmienne przedefiniowane nazywamy zmiennymi pomocniczymi.

Model wielomianowy

Zmienna Y objaśniana jest za pomocą wyrażenia wielomianowego względem zmiennej X. W praktyce n=1,2,3. Dla n=2 model funkcji kwadratowej:

Y = a₀ + a₁X + a₂X² (4)

Równanie (4) może reprezentować funkcję przeciętnego kosztu w zależności od X wielkości produkcji. W tym wypadku zakładamy, że: a₀ > 0, a₂ > 0.

Model logarytmiczny (półlogarytmiczny): Y = a₀ + a₁ln(X) + a₂ln(Z) + 

Model hiperboliczny: Y = a₀ + a₁/X + a₂*Z + 

Modele logarytmiczny i hiperboliczny, są wykorzystywane w analizie konsumpcji jako modele o wykresach będących krzywymi Engla, gdzie Y to konsumpcja, X - dochód, Z - inny parametr.

Model z interakcjami: Y = a₀ + a₁·X + a₂·Z + a₃·X·Z + 

Ogólnie modele z interakcjami uwzględniają to, że wpływ zmiany jednej zmiennej objaśniającej zależy od wartości przyjmowanej przez inne zmienne objaśniające. Uwzględnienie w modelu iloczynu zmiennych objaśniających jest jednym z najprostszych modelu tego typu.

Pochodna cząstkowa Y po X: dY/dX = a₁ + a₃·Z , czyli jest liniową funkcją Z. Jeśli Z będzie interpretowane jako czas Z = t, to krańcowy przyrost M_Y|X = a₁ + a₃·t, będzie liniową funkcją czasu.

Modele linearyzowalne ze względu na parametry strukturalne:

Model potęgowy (podwójnie logarytmiczny, logarytmiczno-liniowy).

Y = a · X^b · Z^c · exp() lub ln(Y) = ln(a) + b*ln(X) + c*ln(Z) + 

Jest to jeden z bardziej popularnych w ekonometrii modeli nieliniowych. Stosowany jest między innymi jako ekonometryczna funkcja produkcji Cobba-Douglasa lub jako ekonometryczna funkcja popytu.

Model wykładniczy (półlogarytmiczny)

Y = exp(a + b·X + ) lub ln(Y) = a + b·X + 

Model wykładniczy stosuje się zwykle do ilustracji wykładniczego wzrostu zmiennej Y względem zmiennej X.

Model S-krzywej (wykładniczo-hiperboliczny)

Y = exp(a + b/X + ) lub ln(Y) = a + b/X + 

Jeśli X jest interpretowane jako czas X=t, to model stosuje się jako model trendu o wykresie zbliżonym do krzywej logistycznej.

Składniki losowe i estymacja modelu

Modele liniowe względem parametrów szacujemy klasyczną metodą najmniejszych kwadratów (KMNK). Jeżeli model podlegał linearyzacji, to przekształceniu podlega również losowe zaburzenie. Możemy stosować metodę najmniejszych kwadratów jeśli przekształcone zaburzenie losowe spełnia wymagania KMNK.

Np. badając model: Y = exp(b·X) · ,

sprowadzamy go do postaci liniowej przekształceniem logarytmicznym: ln(Y) = b*X +ln()

Założenia KMNK wymagają by zmienna ln() miała rozkład normalny o wartości oczekiwanej zero. Oznacza to, że sama zmienna losowa  ma rozkład logarytmiczno-normalny i że w modelu jest zaburzeniem multyplikatywnym, a nie addytywnym.

Funkcja logistyczna i model logitowy

Klasyczna postać modelu krzywej logistycznej to:

; gdzie a>0, b>1, g>0.

Funkcja logistyczna ma następujące własności:

1. 
   , czyli a - to parametr określający poziom nasycenia, maksymalny poziom wartości Y

2. dla t = 0 zachodzi
   

3. Y_t ma punkt przegięcia dla t = ln(b)/g

Funkcja logistyczna ma zastosowanie przy modelowaniu długookresowego wzrostu liczby ludności, reprezentacji wielkości sprzedaży nowego produktu na rynku. Popularność modelu logistycznego zaowocowała powstaniem specyficznych metod estymacji parametrów modelu. Funkcja logistyczna ma zastosowanie przy modelowaniu zmiennych jakościowych tj. przyjmujących wartości z przedziału [0,1]. Jeden z możliwych modeli dla tego typu zmiennej ma postać:

ta postać to pewien typ funkcji logistycznej. Na przykład P może oznaczać procent gospodarstw domowych posiadających jakieś dobro w danej grupie dochodowej, zaś zmienna X to średnia dochodu w dane grupie dochodowej. Ten model wygodnie jest linearyzować przez posługiwanie się zmienną: ln(P/(1-P))

zachodzi bowiem ln( P / (1-P) ) = a + b·X +  oraz należy ona do całego przedziału (-∞, +∞).

Model ten nazywa się modelem logitowym. Logitem nazywa się wielkość ln( P / (1-P) ).

X nazywa się wielkością objaśniającą logit.

Funkcje Törnquista

Funkcje Törnquista należą do rodziny funkcji o wykresie należącej do rodziny krzywych Engla. Przedstawiają wydatki w funkcji dochodów konsumenta. Wyróżniamy cztery typy funkcji Törnquista w zależności od rodzaju potrzeb zaspokajanych konsumpcją określonych dóbr.

1. 
   ; a>0; c>0; b<-c; 0<X≤c lub X>-b; dobra i usługi niższego rzędu.

2. 
   ; a>0; b>0; X>0; dobra podstawowe (pierwszej potrzeby.

3. 
   ; a>0; b>0; c>0; X≥c ; dobra wyższego rzędu (dalszej potrzeby).

4. 
   ; a>0; b>0; c>0; X≥c ; dobra i usługi luksusowe.

Modele segmentowe

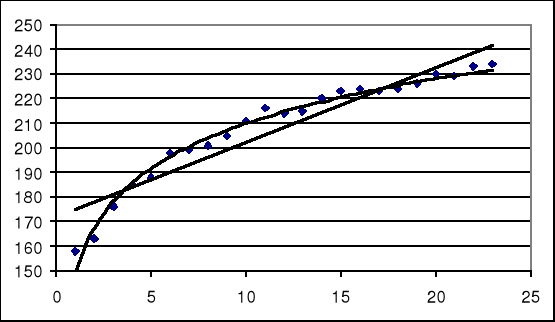
Jeżeli w analizie szeregów czasowych możemy wyodrębnić podokresy, w których zbiory obserwacji łatwo opisują się różnymi modelami ekonometrycznymi, to tworzymy model segmentowy, inny model (segment) na każdym podokresie. Element szeregu czasowego kończący jeden segment i jednocześnie zaczynający następny nazywamy punktem zwrotnym.

Najprostszym przypadkiem jest model kawałkami liniowy, każdy segment to model trendu liniowego.

Przykład 5

Dane tworzą szereg czasowy: Y₁, Y₂,…Y_n. Rozpoznajemy (np. obserwując wykres szeregu czasowego) dwa punkty zwrotne t₁ , t₂ . Na trzech przedziałach czasowych budujemy trzy segmenty trendu liniowego:

Y_t = a₀ + a₁·t +  ; dla t < t₁ ,

Y_t = b₀ + b₁·t +  ; dla t₁ ≤ t < t₂ ,

Y_t = c₀ + c₁·t +  ; dla t₂ ≤ t ,

Funkcja produkcji

Funkcja produkcji wyraża zależność jaka zachodzi między wielkością wytworzonego produktu Y, a czynnikami mającymi wpływ na produkcję X₁, X₂,…X_n oraz zaburzeniem losowym .

Y = f(X₁, X₂,…X_n, )

W dalszych rozważaniach ograniczymy się do dwóch czynników: L - nakładów pracy oraz K - kapitału.

Własności funkcji produkcji

Funkcja produkcji zwykle jest funkcją nieliniową. W dalszym opisie dla uproszczenia opisu pominiemy zaburzenie losowe  oraz przyjmiemy zależność:

Y = f(K,L), gdzie Y>0, K>0, L>0.

Wykres funkcji produkcji tworzy powierzchnię w R³, a dokładnie mówiąc w dodatniej oktancie R³. Może na powierzchni wykresu rozpatrywać warstwice, dla każdej ustalonej wielkości produkcji Y=Y₀. Te linie warstwic będziemy nazywać liniami stałej produkcji (izokwantami produkcji).

Równanie izokwanty ma postać: f(K,L) = Y₀.

W dalszych rozważaniach zakładamy, że funkcja produkcji jest odpowiednio gładka, a mianowicie, że jest dwukrotnie różniczkowalna oraz, że wykres izokwanty jest wypukły (tak, jak wypukły jest wykres funkcji x²). Wypukłość izokwanty oznacza, że jeśli (K₁,L₁) oraz (K₂,L₂) dają taką samą wielkość produkcji:

czyli f(K₁,L₁) = f(K₂,L₂) = Y₀ oraz 0<a<1

to a·f(K₁,L₁) + (1-a)·f(K₂,L₂) ≥ Y₀

Założenia, które powinna spełniać funkcja produkcji:

1. Produkcyjność krańcowa czynnika produkcji jest dodatnia, czyli pochodne cząstkowe spełniają: f_K>0, f_L>0.

Warunek 1. oznacza, że nakłady produkcyjne są efektywne, zwiększenie danego czynnika powoduje wzrost produkcji.

2. Produkcyjność krańcowa jest malejąca względem nakładów danego czynnika, czyli pochodne cząstkowe spełniają: f_KK<0, f_LL<0.

Warunek 2. oznacza, że krańcowe przyrosty maleją w miarę wzrostu danego nakładu, przy nie zmieniającym się drugim nakładzie.

3. Krańcowa produkcyjność jednego czynnika wzrasta przy wzroście drugiego czynnika, czyli pochodne mieszane f_KL = f_LK > 0.

Warunek 3. oznacza, że krańcowe przyrosty rosną przy wzroście obu nakładów.

4. Funkcja f jest jednorodna, czyli: f(aK,al.) = a^r·f(K,L), dla a>0.

Jednorodność funkcji produkcji oznacza można określi, jak zareaguje produkcja na zwiększenie wielkości nakładów. Dla r=1 jest to wzrost proporcjonalny. Dla r>1, jest rosnąca skala produkcji. Dla r<1, malejąca skala produkcji.

5. Czynniki produkcji są wzajemnie zastępowalne (zachodzi substytucja czynników produkcji).

Miarą stopnia substytucji jest krańcowa stopa substytucji czyli pochodna dK/dL lub pochodna dL/dK. Zakładamy, że te wielkości są ujemne.

Jako krańcową stopę wzajemnej substytucji (KSS) między K i L określamy współczynnik nachylenia izokwanty względem osi L:

KSS = dK/dL = -( f_L/f_K )

Współczynnik nachylenia izokwanty względem osi K wynosi:

1/KSS = dL/dK = -( f_K/f_L)

Na podstawie KSS możemy określi o ile powinien się zmienić nakład jednego czynnika, gdy drugi ulegnie zmianie o małą wielkość tak, by produkcję utrzymać na tym samym poziomie.

Jeśli KSS = -0,2 to przy spadku (L) nakładu pracy o jednostkę, należy zwiększyć nakład (K) kapitału o 0,2 jednostki, zaś przy spadku (K) nakładu kapitału o jednostkę, należy zwiększyć nakład (L) pracy o 5 jednostek.

Przykład 6

Dana jest funkcja produkcji Y = 2·(KL)^0,5. Zbadać czy spełnia ona warunki nałożone na funkcję produkcji? Obliczyć f_K , f_L , KSS dla K = 1, L = 4.

Znaczącą rolę w ekonometrii odgrywa funkcja produkcji Cobba-Douglasa postaci:

Y = a₀·X₁^a1· X₁^a2·… X₁^an· ;

gdzie a_i > 0 dla 0 ≤ i ≤ n. Jest to przykład potęgowego modelu ekonometrycznego.

Zbadamy funkcję produkcji Cobba-Douglasa dla przypadki dwuwymiarowego:

Y = a·K^b·L^c· ; dla a>0 ; 0 < b, c < 1.

Do estymacji parametrów strukturalnych wykonujemy transformację logarytmiczną i dostajemy:

ln(Y) = ln(a) + b·ln(K) + c·ln(L) +  ;

Czy spełnia ona wymogi nakładane na funkcję produkcji?

1. f_K = a·b·K^b-1·L^c > 0 ; f_L = a·c·K^b·L^c-1 > 0 ; produkcyjności krańcowe są dodatnie

2. f_KK = a·b·(b-1)·K^b-2·L^c < 0 ; f_LL = a·c·(c-1)·K^b·L^c-2 < 0 ; produkcyjności krańcowe są malejące

3. f_KL = f_LK = a·b·c·K^b-1·L^c > 0 ; produkcyjność jednego czynnika rośnie przy zwiększeniu nakładów drugiego;

4. f(d·K, d·L) = d^b+c ·f(K,L); czyli jest jednorodna stopnia (b+c);

5. KSS = -(f_L/f_K) = -(cK/bL) = -(c/b)·U ; gdzie U = K/L to współczynnik technicznego uzbrojenia pracy,

Wykład 3-4

Funkcja produkcji

Ogólna postać funkcji produkcji: y = f(x₁, x₂,…, x_n, ) ;

gdzie:

y - wielkość produkcji

x₁, x₂,…, x_n - wielkości czynników produkcji

 - składnik losowy

Funkcja produkcji jest podstawowym narzędziem do badania zależności między wielkością produkcji, a wielkościami czynników produkcji. Funkcja produkcji może mieć rozmaite postacie analityczne. Zazwyczaj wymaga się by miała ona pewne podstawowe własności. Często jednak stosuje się również funkcje nie spełniających tych wymagań.

Trzy najczęściej występujące postaci funkcji produkcji to funkcja:

liniowa - y^_t = a₀ + a₁x_1t + a₂x_2t + … + a_nx_nt ;

wielomianowa drugiego stopnia - y^_t = a₀ + a₁x_1t + a₂x²_1t ;

potęgowa -
;

Szczególne znaczenie ze względu na spełnianie wymaganych warunków, ma funkcja produkcji Cobba-Douglasa.

Przykład 10.1 [Borkowski, Dudek, Szczesny]

Nr gospodarstwa	Produkcja końcowa y	Środki trwałe x1	Środki obrotowe x2
1	27.052	171.744	18.745

Na podstawie danych z tabeli 10.1 obliczono parametry strukturalne funkcji produkcji dla modelu liniowego, potęgowego (Cobba-Douglasa) i wielomianowego stopnia drugiego:

Liczymy produkt całkowity dla gospodarstwa nr 19 dla każdego modelu, zgodnie z oszacowaniami tego modelu.

Wartości rzeczywiste wynoszą: y = 69.898 ; x₁ = 216.130 ; x₂ = 33.963 .

Dostajemy wyliczenia:

Dla modelu liniowego: y^ = 16.206,28 + 0,1159∙216.130 + 0,6146∙33.963 = 62.133,8 ;

Dla modelu potęgowego: y^ = 8,32 ∙ 216.130^0,3166 ∙ 33.963^0,4857 = 64.536,3 ;

Dla modelu wielomianowego: y^ = -11.618,8 + 2,04 ∙ 33.963 - 0,000004 ∙ (33.963)² = 53.051,8 .

Obliczone wartości teoretyczne są różne. Najbliższa wartości faktycznej jest wartość oszacowana na podstawie potęgowej funkcji produkcji.

Produkt przeciętny to stosunek wielkości teoretycznej produktu całkowitego do nakładu wielkości czynnika produkcji x_i przy ustalonych wielkościach pozostałych nakladów:

W badanych gospodarstwach w modelu potęgowym, dla gospodarstwa nr 19 przy danych nakładach środków trwałych i obrotowych osiągnięto produkt przeciętny:

PP_x1(216.130; 33.963) = 64.536,3 / 216.130 = 0,30

PP_x2(216.130; 33.963) = 64.536,3 / 33.963= 1,90

W badanych gospodarstwach z 1 złotówki środków trwałych uzyskiwano przeciętnie 0,30zł produkcji końcowej. Z z 1 złotówki środków obrotowych uzyskiwano przeciętnie 1,90zł produkcji końcowej.

Rachunek marginalny (krańcowy)

Interesuje nas wpływ marginalny (krańcowy) daneo czynnika na produkcyjność tego czynnika.

Przyrost krańcowy to odpowiednia pochodna cząstkowa:

Jeśli przyrost krańcowy jest stałą to zmienna X_i w modelu występuje w sposób liniowy.

Przykład

Model liniowy: y = ₀ + ₁x₁ + ₂x₂ +  ;

Przykład

Model potęgowy:

Przykład 10.1 (cd)

Przyrosty krańcowe produkcji względem nakładów na środki obrotowe obliczone na podstawie oszacowanych modeli ekonometrycznych przy stałym poziomie wartości środków trwałych dla wybranych gospodarstw:

Przyrost krańcowy M_Y|Xi można interpretować jako wielkość przyrostu zmiennej Y, gdy zmienna X_i wzrośnie o jednostkę ceteris paribus (pozostałe zmienne pozostaną bez zmian).

Elastyczność cząstkowa to odpowiednia logarytmiczna pochodna cząstkowa:

Jeśli elastyczność cząstkowa jest stałą to zmienna X_i w modelu występuje w sposób potęgowy. Elastyczność cząstkową M_Y|Xi można interpretować jako wielkość przyrostu względnego (procentowego) zmiennej Y, gdy zmienna X_i wzrośnie o jeden procent ceteris paribus (pozostałe zmienne pozostaną bez zmian).

Przykład

Model potęgowy (logarytmiczno-liniowy): y = x₁^x₂^γe^ ;

Do oszacowania elastyczności cząstkowej często używa się następującego wzoru:

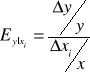
Przykład 10.1 (cd)

Dla gospodarstwa nr 21 znamy wielkości y = 42.491; x₁ = 26.569 z roku 1999 (poprzedniego). Obliczamy elastyczność cząstkową:

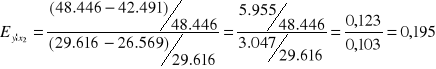
Efekt skali produkcji (elastyczność skali produkcji)

Efektem skali produkcji nazywamy sumę wszystkich elastyczności cząstkowych:

Wykład 5-6

Wielorównaniowe modele ekonometryczne

Przy analizie złożonych zjawisk ekonometrycznych model jednorównaniowy tłumaczący kształtowanie się jednej zmiennej objaśnianej może być niewystarczający. Może być tak, że pojedyncze równanie jest częścią układu relacji opisywanego zespołem relacji. W takim wypadku konstruujemy model wielorównaniowy - zespół równań. Każde z równań wyjaśnia kształtowanie się jednej zmiennej objaśnianej. Ze względu na sprzężenie między wielkościami występującymi w modelu, zmienna objaśniana w jednym równaniu, może być objaśniającą w innym równaniu.

Wyróżniamy dwa podstawowe sposoby zapisu modeli wielorównaniowych. Zapis w postaci strukturalnej i zapis w postaci zredukowanej.

Postać strukturalna oddaje strukturę związków między zmiennymi. Każde równanie w tej postaci objaśnia jedną zmienną pozostałymi zmiennymi. Postać strukturalna jest „naturalną” postacią modelu.

Przypomnienie

Zmienne pojawiające się w równaniach modelu dzielimy na:

1. zmienne objaśniane, objaśniające;

2. zmienne endogeniczne, egzogeniczne;

3. zmienne bieżące, opóźnione.

Podział na zmienne objaśniane i objaśniające, to podział określany na poziomie pojedynczego równania.

Podział na zmienne endogeniczne i egzogeniczne, to podział określany na poziomie całego modelu. Zmienne endogeniczne to te, które są objaśniane modelem (w jakimś równaniu modelu). Zmienne egzogeniczne określane są poza modelem (nie są objaśniane żadnym równaniem).

W dynamicznym modelu wielorównaniowym mogą występować zmienne z różnych okresów. Endogeniczne i egzogeniczne zmienne mogą być nieopóźnione, czyli z okresu bieżącego, jak i opóźnione, czyli z okresów wcześniejszych.

Zmienne endogeniczne nieopóźnione nazywa się zmiennymi łącznie współzależnymi.

Zmienne egzogeniczne i opóźnione endogeniczne nazywamy zmiennymi z góry ustalonymi, na ich podstawie wyliczamy wartości obecne zmiennych endogennych.

Zmienne	Nieopóźnione	Opóźnione
Endogeniczne	Łącznie współzależne
Egzogeniczne		Z góry ustalone

Podział na zmienne łącznie współzależne i z góry ustalone jest ważny z względu na szacowanie parametrów modelu.

Zazwyczaj równania modelu są unormowane, czyli tak zbudowane by współczynnik przy zmiennej endogenicznej nieopóźnionej objaśnianej w danym równaniu był równy 1.

W postać zredukowanej modelu w każdym równaniu występuje tylko jedna zmienna endogeniczna nieopóźniona, ta która jest wyjaśniana równaniem, wszystkie pozostałe zmienne są z góry ustalone. Postać zredukowana jest wygodna do szacowania parametrów modelu.

Przykład 1

Rozpatrujemy model ekonometryczny dany równaniami:

C_t = ₀ + ₁·Y_t + _t (1)

Y_t = C_t + I_t + G_t (2)

Gdzie C_t - zagregowana konsumpcja,

Y_t - dochód narodowy,

_t - składnik losowy,

I_t - inwestycje,

G_t - wydatki rządowe.

Równanie (1) jest równaniem stochastycznym (uwzględniającym czynnik losowy). Opisuje wielkość zagregowanej konsumpcji przy pomocy wielkości dochodu narodowego zaburzonego czynnikiem losowym.

Równanie (2) ma charakter bilansowy. Wiąże dochód narodowy z konsumpcją, inwestycjami i wydatkami rządowymi.

Model wyjaśnia wielkości opisywane w chwili t. Nie pojawiają się żadne wielkości z innych chwil, nie ma wielkości opóźnionych.

C_t , Y_t są zmiennymi endogenicznymi nieopóźnionymi.

G_t , I_t są zmiennymi egzogenicznymi nieopóźnionymi.

W równaniu (1) C_t jest zmienną objaśnianą, Y_t zmienną objaśniającą.

W równaniu (2) Y_t jest zmienną objaśnianą, C_t , I_t , G_t zmiennymi objaśniającymi.

Zmiennymi z góry ustalonymi są nieopóźnione zmienne egzogeniczne I_t , G_t .

Przykład 2

Rozpatrujemy model ekonometryczny dany równaniami:

C_t = ₀ + ₁ · Y_t + _1t (3)

Y_t = ₀ + ₁·C_t + ₂·I_t-1 + _2t (4)

Gdzie C_t - zagregowana konsumpcja,

Y_t - dochód narodowy,

_1t , _2t - składniki losowe,

I_t - inwestycje,

Model wyjaśnia wielkości opisywane w chwili t.

Równanie (3) ma taką samą postać ja równanie (1).

Równanie (4) wiąże wielkość dochodu z konsumpcją i poziomem inwestycji w roku poprzednim. Uwzględnia wpływ czynnika losowego.

C_t , Y_t są zmiennymi endogennymi nieopóźnionymi. G_t , I_t są zmiennymi egzogennymi nieopóźnionymi, zaś I_t-1 jest zmienną egzogenną opóźnioną.

W równaniu (4) Y_t jest zmienną objaśnianą, C_t oraz zmienna opóźniona I_t-1 są zmiennymi objaśniającymi.

Jedyną zmienną z góry ustaloną w modelu jest opóźniona zmienna egzogeniczna I_t-1 .

Przykład 3

Jeślibyśmy zmodyfikowali przykład 2 uznając, że poziom dochodu Y_t objaśnia C_t-1 konsumpcja z roku ubiegłego, a nie C_t konsumpcja z roku bieżącego, to model miałby postać:

C_t = ₀ + ₁·Y_t + _1t (5)

Y_t = ₀ + ₁·C_t-1 + ₂·I_t-1 + _2t (6)

W tym modelu nieopóźnione zmienne endogeniczne są takie same jak w modelu z przykładu 2. Zbiór zmiennych z góry ustalonych tworzą zaś opóźnione o rok: konsumpcja z roku ubiegłego C_t-1 (zmienna endogeniczna) oraz inwestycje z roku ubiegłego I_t-1 (zmienna egzogeniczna).

Postać strukturalna modelu.

Oznaczmy:

y_ti - obserwacja i-tej zmiennej endogenicznej w chwili t

z_tj - obserwacja j­-tej zmiennej z góry ustalonej w chwili t;

jeśli w równaniu występują stałe, to wprowadzamy fikcyjną zmienną stale równą jeden

i = 1, 2,…, m; j = 1, 2,…, k;

……

Przenoszą wszystkie zmienne współzależne i z góry ustalone na jedną stronę dostajemy:

……

Wprowadzając zapis macierzowy możemy postać strukturalną modelu zapisać równaniem macierzowym:

BY_t + Z_t = _t ; t = 1, 2, …

gdzie:

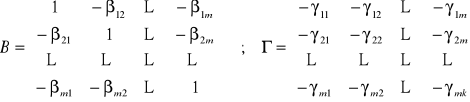
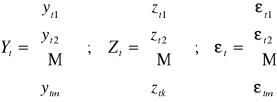
Przykład 4

Niech Y_t = (Y_1t , Y_2t)^T dwuwymiarowy wektor zmiennych endogenicznych oraz niech Z_t = (1 , Z_1t , Z_2t , Z_3t)^T czterowymiarowy wektor zmiennych egzogenicznych rozszerzony przez dodanie stałej do wektora trzywymiarowego.

Niech model ekonometryczny ma postać:

Y_1t = ₁₂·Y_2t + γ₁₀ + γ₁₁·Z_1t + γ₁₂·Z_2t +γ₁₃·Z_3t + _1t

Y_2t = ₂₁·Y_1t + γ₂₀ + γ₂₁·Z_1t + γ₂₂·Z_2t +γ₂₃·Z_3t + _2t

Postać powyższa jest postacią strukturalną modelu.

Przenosząc zmienne egzogeniczne zmienne współzależne i z góry ustalone na lewą stronę, możemy przedstawić model w postaci macierzowej:

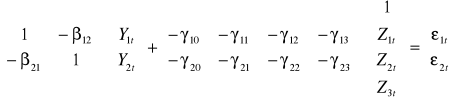
B·Y_t + ·Z_t = _ (7)

To postać strukturalna modelu w zapisie macierzowym.

Postać zredukowana modelu

W postaci zredukowanej zmiennymi objaśniającymi są jedynie zmienne z góry ustalone. W postaci macierzowej:

B·Y_t + ·Z_t = _t

B^-1·B ·Y_t + B^-1··Z_t = B^-1·_t

Y_t = -B^-1··Z_t + B^-1·_t

Y_t = ·Z_t + _t

gdzie:  = -B^-1·· ; _t = B^-1·_t ;

Przykład 5

Badamy model strukturalny złożony z dwóch równań:

k_t = ₁₂ z_t + ₁₃ i_t + ₁ + _1t

z_t = ₂₁ k_t + ₂₂ p_t + ₂ + _2t

Gdzie:

k_t - wartość majątku trwałego w okresie t;

z_t - liczba zatrudnionych w okresie t;

i_t - wartość nakładów inwestycyjnych w okresie t;

p_t - wielkość produkcji w okresie t;

_jt - wielkość składnika losowego w okresie t równania j-tego.

Postać macierzowa modelu strukturalnego:

k_t - ₁₂ z_t - ₁₃ i_t - ₁ = _1t

-₂₁ k_t + z_t - ₂₂ p_t - ₂ = _2t

B·Y_t + ·Z_t = _t

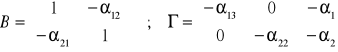
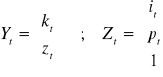
Postać zredukowana: Y_t = ·Z_t + _t

 = -B^-1·· ; musimy najpierw obliczyć det (B) = 1 + ₂₁ ₁₂ ;

a więc

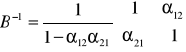
skąd

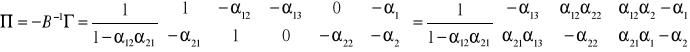
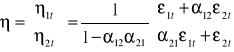
Klasyfikacja modeli wielorównaniowych.

Modele wielorównaniowe dzielimy na trzy rozłączne klasy ze względu na powiązania występujące między nieopóźnionymi zmiennymi endogenicznymi:

1. modele proste,

2. modele rekurencyjne,

3. modele o równaniach współzależnych.

Model jest modelem prostym jeśli zmienne endogeniczne nieopóźnione nie są ze sobą wzajemnie powiązane.

Model jest modelem rekurencyjnym jeśli powstaje łańcuch zmiennych endogenicznych nieopóźnionych. W równaniach objaśniających zmienną Y_kt pojawiają się zmienne Y_jt dla j<k, nie pojawiają się zaś dla j>k.

Model jest modelem o zmiennych współzależnych jeśli nie jest ani modelem prostym, ani rekurencyjnym. W tym modelu pojawiają się zmienne nieopóźnione endogeniczne jednocześnie od siebie zależne.

Proste metody ustalania z jakim modelem mamy do czynienia.

Metoda wykorzystująca schemat strzałkowy

Rysujemy graf zorientowany, którego wierzchołki numerujemy zmiennymi endogenicznymi nieopóźnionymi. Z wierzchołka Y­_i do wierzchołka Y_k rysujemy strzałkę skierowaną, jeśli zmienna Y_i jest zmienną objaśniającą w równaniu wyjaśniającym dla zmiennej Y_k.

Jeśli w grafie nie ma żadnych strzałek to jest to model prosty. Jeśli strzałki tworzą powiązania bez pętli, to jest to model rekurencyjny. Jeśli pojawia się przynajmniej jedna pętla to jest to model o równaniach współzależnych.

Metoda wykorzystująca kształt macierzy parametrów B.

Jeżeli możemy tak przenumerować zmienne i równania w modelu, by macierz współczynników przy nieopóźnionych zmiennych endogenicznych była:

1. diagonalna, to rozważany model jest modelem prostym,

2. trójkątna, to rozważany model jest modelem rekurencyjnym,

3. jeśli nie możemy osiągnąć ani macierzy diagonalnej, ani trójkątnej to model jest modelem o równaniach współzależnych.

Przykład 5 Rozważamy model z przykładu 2 zmieniając oznaczenia parametrów i dokonując przekształceń:

C_t = ₀ + ₁ · Y_t + _1t (3)

Y_t = ₀ + ₁·C_t + ₂·I_t-1 + _2t (4)

C_t - ₁·Y_t = ₀ + _1t (3`)

-₁·C_t + Y_t = ₀ + ₂·I_t-1 + _2t (4')

C_t + ₁₂·Y_t = γ₁₀ + _1t (3``)

₂₁·C_t + Y_t = γ₂₀ + γ₂₁·I_t-1 + _2t (4'')

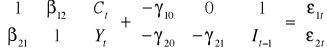
Macierz współczynników B przez zmianę numeracji nie da się sprowadzić do postaci diagonalnej, ani trójkątnej. Rozważany model jest więc modelem o równaniach współzależnych.

Posługując się schematem strzałkowym dostajemy:

C_t ↔Y_t

A więc również widzimy, że jest to modelem o równaniach współzależnych.

Jest to również model dynamiczny, w równaniach pojawiają się wartości opóźnione.

Przykład 6 Rozważamy model z przykładu 3 zmieniając oznaczenia parametrów:

C_t = ₀ + ₁ · Y_t + _1t (5)

Y_t = ₀ + ₁·C_t-1 + ₂·I_t-1 + _2t (6)

C_t + ₁₂·Y_t = γ₁₀ + _1t (5`)

Y_t = γ₂₀ + γ₂₁·C_t-1 + γ₂₂·I_t-1 + _2t (6')

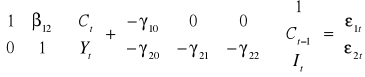
Macierz współczynników B jest w postaci trójkątnej. Rozważany model jest więc modelem rekurencyjnym.

Posługując się schematem strzałkowym dostajemy:

Y_t → C_t

A więc również widzimy, że jest to modelem rekurencyjny.

Jest to również model dynamiczny, w równaniach pojawiają się wartości opóźnione.

Przykład 7

Badamy model dany równaniami:

Y_1t = ₁₀ + ₁₁X_1t + ₁₂Y_2t + _1t (11)

Y_2t = ₂₀ + ₂₁X_1t + ₂₂Y_1t + _2t (12)

Wyznacz zmienne endogeniczne, egzogeniczne, objaśniane i objaśniające, z góry ustalone.

Czy w modelu występują zmienne opóźnione?

Czy to jest model dynamiczny, czy statyczny?

Jaka jest postać strukturalna tego modelu w zapisie macierzowym?

Odpowiedź:

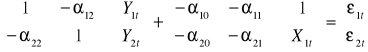
Jaki to jest typ modelu ze względu na charakter powiązań między zmiennymi endogenicznymi nieopóźnionymi?

Odpowiedź na podstawie postaci macierzy współczynników przy zmiennych endogenicznych nieobciążonych - model o równaniach łącznie współzależnych.

Y₁ ↔ Y₂

Odpowiedź na podstawie schematu strzałowego.

Przykład 8

Badamy model dany równaniami:

Y_1t = ₁₀ + ₁₁X_1t + ₁₂Y_2,(t-1) + _1t (13)

Y_2t = ₂₁X_1t + ₂₂Y_1t + _2t (14)

Czy jest to model statyczny czy dynamiczny?

Dynamiczny. Co prawda nie występuje samodzielnie czynnik czasu, ale są zmienne opóźnione.

Czy w modelu są zmienne endogeniczne nieopóźnione?

W każdym modelu są zmienne endogeniczne nieopóźnione. W tym modelu to są: Y_1t , Y_2t .

Czy w modelu są zmienne endogeniczne opóźnione?

Jest : Y_2,(t-1) .

Czy w modelu są zmienne egzogeniczne nieopóźnione?

Są: 1 , X_1t . Komentarz: stała 1 jest traktowana jak stała zmienna egzogeniczna.

Czy w modelu są zmienne egzogeniczne opóźnione?

W tym modelu nie ma.

Jaki to jest model ze względu na charakter powiązań między zmiennymi endogenicznymi nieopoźnionymi?

To jest model o równaniach rekurencyjnych. Macierz współczynników przy zmiennych nieopóźnionych endogenicznych jest trójkątna. W schemacie strzałowym są strzałki lecz nie ma pętli.

Są dwie zmienne endogeniczne Y₁ , Y₂ . Są dwie zmienne egzogeniczne 1 , X₁ .

Estymacja parametrów modeli wielorównaniowych

W modelu jednorównaniowym, przy spełnieniu odpowiednich założeń, do estymacji parametrów strukturalnych posługujemy się metodą najmniejszych kwadratów (MNK).

W modelu wielorównaniowym niestety nie zawsze możemy tak postąpić.

Kiedy możemy? Możemy w modelu prostym. Brak tu powiązań między zmiennymi endogenicznymi nieopóźnionymi występującymi w poszczególnych równaniach modelu. Każde równanie możemy traktować tak, jakby było osobnym modelem jednorównaniowym. W każdym równaniu, jeżeli tylko spełnione są założenia MNK, szacujemy parametry strukturalne metodą najmniejszych kwadratów (MNK).

W tym wypadku mówimy o metodzie estymacji pojedynczej, po kolei estymowaliśmy parametry równanie po równaniu.

W przypadku modelu rekurencyjnego możemy postąpić następująco. Przenumerowujemy równania tak, by w pierwszym występowała tylko jedna zmienna endogeniczna nieopóźniona. W kolejnych zaś równaniach dochodziła następna zmienna endogeniczna nieopóźniona.

(a) Y_1t = ₁₀ + ₁₁·X_1t + _1t

(b) Y_2t = ₂₀ + ₂₁·X_2t + ₂₂·Y_1t + _2t

(c) Y_3t = ₃₀ + ₃₁·X_2t + ₃₂·Y_1t + ₃₃·Y_1t + _3t

Parametry równania (a) szacujemy standardowo metodą MNK.

Niech:

(a') Y^_1t = ^₁₀ + ^₁₁·X_1t

Równanie teoretyczne wyliczone na podstawie obserwacji zmiennej Y₁.

Parametry równania (b) szacując na podstawie obserwacji Y₂ i wartości teoretycznych Y^₁ (zamiast Y₁). W ten sposób omijamy trudności związane z występowaniem zmiennej Y₁ (losowość).

Analogicznie postępujemy z kolejnymi równaniami. Do estymacji parametrów kolejnego równania, pozbywamy się kolejnych zmiennych endogenicznych nieopóźnionych, wstawiając w ich miejsce ich estymaty. Tak krok po kroku dostajemy estymaty nieobciążone parametrów strukturalnych kolejnych równań.

Jak postępujemy, gdy model jest modelem o równaniach łącznie współzależnych. Sprowadzamy model do postaci zredukowanej. W postaci zredukowanej badany model jest modelem prostym. Jeśli składniki losowe z różnych równań są niezależne stosujemy do każdego z nich metodę najmniejszych kwadratów.

Wykład 7

Podstawy analizy szeregów czasowych.

Modele ekonometryczne dzielimy na dynamiczne i statyczne.

Dynamiczne modele ekonometryczne pozwalają na badanie zmian obserwowanego zjawiska w czasie. Cechą modeli dynamicznych jest uwzględnienie wpływu czasu w sposób jawny, w tym również poprzez uwzględnienie zmieniających się w czasie relacji między zmiennymi. Wyróżnimy dwa typy modeli dynamicznych:

1. modele dla których jedną ze zmiennych objaśniających (egzogenicznych) jest czas (zazwyczaj oznaczany przez t = 1, 2,…,n)

• w tej grupie wyróżniamy modele z czasem jako jedyną zmienną objaśniającą, są to rozmaitego typu modele trendu (modele tendencji rozwojowej);

2. modele w których wpływ czasu uwzględniony jest poprzez zmienne opóźnione.

Modele trendu

Trend to trwała tendencja wzrostowa lub spadkowa dla poziomu określanego zjawiska. Wygodne do opisu i badania są następujące analityczne modele trendu:

1. Trend liniowy: y_t = a + b · t + 

2. Trend wykładniczy: y_t = a · b^t · 

3. Trend potęgowy: y_t = a · t^b · 

4. Trend logarytmiczny: y_t = a + b · ln(t) + 

5. Trend logistyczny
   ; gdzie a>0, b>1, g>0.

Modele trendu 2-5 są modelami nieliniowymi, ale jak zauważyliśmy na wcześniejszym wykładzie są linearyzowalne. Stąd ich popularność w ekonometrii. Po linearyzacji, metodą najmniejszych kwadratów możemy estymować parametry równań. Jeśli obserwowana jest zmienność tendencji wraz z upływem czasu, to staramy się stosować modele segmentowe do opisu tendencji.

Przykład 1

Po zlogarytmowaniu modelu trendu wykładniczego (2.) dostajemy równanie:

ln(y_t) = ln(a) + t · ln(b) + ln(

po podstawieniu:

z_t = ln(y_t); A = ln(a); B = ln(b);   ln(

dostajemy

z_t = A + t · B + 

Załóżmy, że metodą najmniejszych kwadratów, na podstawie obserwacji, dokonujemy estymacji parametrów:

A^ = 1,25; B^ = 0,25.

Tak więc za estymatory parametrów a, b przyjmujemy:

a^ = exp(1,25) = 3,49; b^ = exp(0,25) = 1,28.

Jak już wielokrotnie zauważyliśmy wartość poznawcza modelu trendu nie jest duża. Może być on używany do prognozowania lub wyznaczania kierunku i tempa zmian. Często używany jest w syntetycznej analizie dynamiki zjawiska.

Modele ze zmiennymi opóźnionymi

Zmienne opóźnione zarówno objaśniające jak i objaśniane występują bardzo często w modelach ekonometrycznych. Często wpływ zmiennych objaśniających nie jest natychmiastowy jak np. zmiana wielkości sprzedaży pod wpływem reklamy, inflacji czy wzrostu zarobków.

Wśród przyczyn występowania opóźnienia wymienia się między innymi:

1. Przyczyny psychologiczne: przyzwyczajenia, bezwładność zachowań, koszt dostosowania, niepewność stałości zmian;

2. Przyczyny technologiczne: zmiany technologii wymagają czasu, często upewnienia się w trwałości trendu zmian;

3. Przyczyny instytucjonalno-prawne: zawarte umowy, zobowiązania, kontrakty, lokaty.

Model z rozkładem opóźnień z jedną zmienną objaśniającą:

y_t =  + ₀ · x_t + ₁ · x_t-1 + … + _n · x_t-n + _t

W tym modelu jest tylko jedna zmienna wyjaśniająca, ale wartość zmiennej wyjaśnianej jest opisywana przez zmienną wyjaśnianą i jej wartości opóźnione. Współczynniki ₁, ₂, …, _n mierzą wpływ kolejnych opóźnień na zmiennej objaśniającej na wielkość zmiennej objaśnianej. Zazwyczaj wpływ wartości opóźnionych jest coraz mniejszy. Często jako wystarczające przybliżenie w modelu przyjmujemy wpływ tylko kilku opóźnień.

Model w którym przyjmujemy, że opóźnienie wynosi co najwyżej dwa okresy:

y_t = a + ₀ · x_t + ₁ · x_t-1 + _t

Model w którym dopuszczamy nieskończoną ilość opóźnień:

y_t = a + ₀ · x_t + ₁ · x_t-1 + … + _n · x_t-n + …+ _t

Współczynnik ₀ nazywamy mnożnikiem krótkookresowym (krótkookresową krańcową skłonnością do konsumpcji), określa on średnią zmianę zmiennej objaśnianej Y wynikająca z jednostkowej zmiany zmiennej objaśniającej X dokonanej w tym samym czasie co obserwowana zmiana Y.

Zazwyczaj sądzimy, że wpływ zmiennej X maleje z czasem, czyli kolejne współczynniki _i są coraz mniejsze co do wartości bezwzględnej.

Sumę wszystkich współczynników:

 = ₀ + ₁ + … + _n

nazywamy mnożnikiem długookresowym i interpretujemy jako zmianę zmiennej objaśnianej „y” pod wpływem długookresowej jednostkowej zmiany - jednostkowego przyrostu wszystkich wartości bieżących i opóźnionych, zmiennej objaśniającej.

Przykład 2

Pracownik dostając podwyżkę zwiększa swoją konsumpcję. Robi to jednak z opóźnieniem. Przypuśćmy, że następujący model opisuje wielkość wydatków na konsumpcję:

C_t = A + 0,5 · Y_t + 0,25 · Y_t-1 + 0,1 · Y_t-2 + _t

gdzie C_t - wielkość wydatków na konsumpcję w chwili t ;

Y_t - dochód w chwili t,

A - stała.

Przypuśćmy, że pracownik mający dotychczas stałe zarobki w wysokości Y zł, dostał podwyżkę w wysokości K zł. Jak będzie zmieniać się jego konsumpcja?

0. Jeden miesiąc przed podwyżką i wcześniej - miesiąc (t-1), (t-2), (t-3):

1. C_t-1 = A + 0,5·Y + 0,25·Y + 0,1·Y + _t-1 = A + 0,85·Y + _t-1 = C + _t-1

2. C_t-2 = A + 0,5·Y + 0,25·Y + 0,1·Y + _t-2 = C + _t-2

3. C_t-3 = A + 0,5·Y + 0,25·Y + 0,1·Y + _t-3 = C + _t-3

1. W miesiącu podwyżki - miesiąc t

1. C_t = A + 0,5·(K+Y) + 0,25·Y + 0,1·Y + _t = C + 0,5·K + _t

2. Miesiąc po podwyżce - miesiąc (t + 1)

1. C_t+1 = A + 0,5·(K+Y) + 0,25·(K+Y) + 0,1·Y + _t+1 = C + 0,5·K + 0,25·K + _t+1 = C + 0,75·K + _t+1

3. Dwa miesiące po podwyżce i później - miesiąc (t+2), (t+3), (t+4):

1. C_t+2 = A + 0,5·(K+Y) + 0,25·(K+Y) + 0,1·(K+Y) + _t+2 = C + 0,75·K + 0,1·K +_t+2 = C + 0,85·K + _t+2

2. C_t+3 = A + 0,5·(K+Y) + 0,25·(K+Y) + 0,1·(K+Y) + _t+3 = C + 0,85·K + _t+3

3. C_t+4 = A + 0,5·(K+Y) + 0,25·(K+Y) + 0,1·(K+Y) + _t+4 = C + 0,85·K + _t+4

W pierwszym miesiącu wydatki wzrosną o 0,5·K. W drugim dodatkowo o 0,25·K. W trzecim jeszcze o 0,1·K. Czyli w wzrost dochodów o 1 złotówkę spowoduje natychmiastowy wzrost wydatków o 50 groszy. Po miesiącu wydatki wzrosną o 75 groszy, zaś długookresowy wzrost (po dwóch miesiącach) wyniesie 85 groszy.

Mnożnik krótkookresowy wynosi więc 0,5. Mnożnik długookresowy zaś 0,5 + 0,25 + 0,1 = 0,85.

Przyrosty względne to:

1. Względny przyrost natychmiastowy (w miesiącu podwyżki):
   czyli 58,8% ogólnego efektu wzrostu konsumpcji;

2. Względny przyrost po miesiącu od podwyżki:
   czyli 88,2% ogólnego efektu wzrostu konsumpcji;

3. Względny przyrost po 2 miesiącach od podwyżki:
   czyli 100% ogólnego efektu wzrostu konsumpcji. Nastąpił już cały efekt wywołany podwyżką.

Przykład 2 (cd) przykład liczbowy

Zakładamy model opisany w przykładzie 2. Jan Kowalski dostał podwyżkę w wysokości 400 zł. Obliczyć jak bezwzględnie i względnie wzrastała konsumpcja pana Jana w kolejnych miesiącach po podwyżce.

W miesiącu podwyżki konsumpcja wzrosła o 0,5 · 400 = 200 zł. W pierwszym miesiącu po podwyżce konsumpcja wzrosła o kolejne 0,25 · 400 = 100 zł. W drugim miesiącu po podwyżce konsumpcja wzrosła o kolejne 0,1 · 400 = 40 zł.

Całkowity wzrost konsumpcji po dwóch miesiącach to: 200 + 100 + 40 = 340 zł.

Kolejne przyrosty względne to:

Miesiąc 0:
;

Miesiąc 1:
;

Miesiąc 2:

Koniec przykładu 2.

Model autoregresyjny

Jeżeli zmienną objaśniającą jest opóźniona o jeden okres zmienna wyjaśniana:

Y_t = a + b · Y_t-1 + _t ;

to model taki nazywamy modelem autoregresyjnym pierwszego rzędu.

Model z n opóźnieniami- model autoregresyjny n-tego rzędu ma postać:

Y_t = a + b₁ · Y_t-1 + b₂ · Y_t-2 +…+ b_n · Y_t-n + _t ;

Przykład 3 (model uproszczony)

Załóżmy, że posługujemy się następującym modelem opisującym popyt na pieniądz w zależności od oczekiwanej stopy procentowej:

Y_t = a + b·R_t + _t

gdzie Y_t - popyt na pieniądz w okresie t

R_t - oczekiwana w okresie t (długookresowa) stopa procentowa (stopa procentowa, która będzie obowiązywać w okresie t+1).

Rozważany model ekonometryczny związany jest z hipotezą mówiącą, że popyt na pieniądz zależy od długookresowej stopy procentowej. W okresie t nie znamy jednak R_t, znamy jedynie r_t aktualną w okresie t stopę procentową. Przyjmujemy następującą hipotezę co do kształtowania się oczekiwanej długookresowej stopy procentowej:

R_t - R_t-1 = g · (r_t - R_t-1)

gdzie:

r_t - faktyczna stopa procentowa w chwili t

g - współczynnik korygujący, 0 < g < 1.

Ta hipoteza mówi, że przedmioty gospodarcze korygują swe oczekiwania, uwzględniając dotychczasowe doświadczenia.

Model pozwala oszacować stopę procentową R i użyć ją w modelu opisującym kształtowanie się popytu na pieniądz.

Przykład 3 (cd) przykład liczbowy

W ubiegłym miesiącu (t-1) oczekiwaliśmy, że stopa procentowa wyniesie 4,2%. Jednak po miesiącu okazało się, że wynosi tylko 3,8%. Współczynnik korygujący w naszym modelu wynosi g = 0,8.

Zgodnie z naszym modelem jako oczekiwaną stopę procentową przyjmiemy:

R_t - R_t-1 = g · (r_t - R_t-1)

R_t = R_t-1 + g · (r_t - R_t-1)

R_t = R_t-1 + g · r_t + (1-g) · R_t-1

R_t = 0,8 · 3,8% + 0,2 · 4,2% = 3,04% + 0,84% = 3,88%

Taki model będący przykładem modelu autoregresyjnego, nazywamy modelem oczekiwań adaptacyjnych.

Koniec przykładu 3.

Jeżeli w modelu występują zarówno opóźnienia zmiennej objaśnianej jak i objaśniającej to nazywamy go autoregresyjnym modelem z rozkładem opóźnień:

Y_t = a + b₁ · Y_t-1 + b₂ · Y_t-2 + … + b_k · Y_t-k + c₀ · X_t + c₁ · X_t-1 + … + c_n · X_t-n + _t .

Przykład 4

C_t = a + b₁ · C_t-1 + b₂ · C_t-2 + c₀ · PKB_t + c₁ · PKB_t-1 + _t .

Model tłumaczący wielkość zagregowanej konsumpcji, wielkością konsumpcji opóźnionej do dwóch okresów oraz wielkością produktu krajowego brutto z obecnego okresu i o jeden opóźnionego.

Model z nieskończonym rozkładem opóźnień

Model Koycka

Przyjmujemy, że w modelu występuje nieskończony rozkład opóźnień:

y_t = a + c₀ · x_t + c₁ · x_t-1 + … + c_n · x_t-n + … + _t .

Nieskończony rozkład opóźnień może opisywać sytuację, gdy nie jest nam znana wielkość opóźnienia.

Można by budować model sekwencyjnie ze wzrastającą ilością opóźnień metodą najmniejszych kwadratów (MNK), aż do chwili, gdy kolejne opóźnienie okazałoby się nieistotne. Jest to jednak metoda żmudna i pracochłonna. Dodatkowo wzrasta ilość parametrów do szacowania, maleje ilość stopni swobody. Zmienne opóźnione mogą być współliniowe.

Jeśli założymy, że parametry c_k maleją w sposób geometryczny, czyli, że zachodzi równanie:

c_k = c₀ · ^k dla k = 0, 1, 2, … , gdzie 0 <  < 1.

To możemy przejść do modelu nazywanego modelem Koycka

Przekształcamy:

y_t = a + c₀·x_t + c₀·¹·x_t-1 + … + c₀·ⁿ·x_t-n + … + _t

y_t = a + c₀·x_t - ·a + · a + c₀·¹·x_t-1 + … + c₀·ⁿ·x_t-n + … + ·_t-1 - ·_t-1 + _t

y_t = a + c₀·x_t - ·a + ·( a + c₀·x_t-1 + … + c₀·ⁿ·x_t-n + … + _t-1 ) + _t - ·_t-1

y_t = a·(1-) + c₀·x_t + ·y_t-1 + (_t - ·_t-1) .

y_t = b + c₀·x_t + ·y_t-1 + _t .

gdzie:

b = a·(1-) ; _t = (_t - ·_t-1) .

Parametr  nazywamy stopą zaniku rozkładu opóźnień.

Tak przekształcony model nazywamy modelem Koycka. Przekształcenie nazywamy transformacją Koycka. Transformacja Koycka przeprowadziła od modelu z nieskończonym rozkładem opóźnień do modelu z opóźnioną o jeden okres zmienna objaśniana, a więc do modelu autoregresjnego.

Mnożnik długookresowy w modelu Koycka wynosi:

Przykład 5

Załóżmy, że zagregowana funkcja konsumpcji C_t w makroekonomicznym modelu równowagi wyrażana jest przez bieżącą i przez opóźnione wartości dochodów do dyspozycji Y_t.

Zakładamy, że współczynniki tej funkcji są dodatnie, malejące geometrycznie. Możemy więc zastosować transformację Koycka, a więc możemy uznać, że zachodzi równanie:

C_t = a · (1 - ) + b₀ · Y_t +  · C_t-1 + _t

Oszacowany na podstawie danych z lat 1964 - 1994 model dla gospodarki USA ma postać w mld USD:

C_t^{^} = -38,11 + 0,52 · Y_t + , · C_t-1

(0,12) (0,12)

R² = 0,988

Wrócimy teraz do modelu wyjściowego:

C_t = a + c₀·Y_t + c₀·¹·Y_t-1 + … + c₀·ⁿ·Y_t-n + … + _t

Możemy wyznaczyć estymaty parametrów modelu:

 = 0,46 ;

a · (1 - ) = -38,11 skąd a = -38,11 / (1 - 0,46) = -38,11 / 0,54 = -70,57 ;

b₀ = 0,52 ; skąd b_n = 0,52 · (0,46)ⁿ ;

b₁ = 0,2392;

b₂ = 0,11;

b₃ = 0,0506

Skąd dostajemy równanie:

C_t^{^} = -70,57 + 0,52 · Y_t + , · Y_t-1 + , · Y_t-2 + , · Y_t-3 + …

Z mnożnikiem długookresowym b = b₀ / (1 - ) = 0,52 / (1 - 0,46) = 0,52 / 0,54 = 0,96 .

Czyli wzrost dochodów do dyspozycji o 1 mld USD powoduje ostatecznie w długim okresie czasu wzrost konsumpcji o 0,96 mld USD. Mnożnik krótkookresowy wynosi zaś 0,52 a więc zachodzi duża bezwładność wydatków względem dochodu.

Wykład 8

Badanie własności odchyleń losowych

Szacowaniu parametrów modelu ekonometrycznego dokonujemy na podstawie założeń MNK. Czy przyjęcie tych założeń było słuszne? Czy trafnie został dobrany model analityczny? Skupimy się teraz na analizie odchyleń losowych w modelu. Narzędziem będą testy statystyczne. Będziemy weryfikować hipotezy związane z szacowaniem ciągu reszt odchyleń losowych modelu.

Badanie losowości

Weryfikacja hipotezy o losowości rozkładu odchyleń losowych ma na celu ocenę trafności doboru postaci analitycznej modelu.

Weryfikujemy hipotezę H₀ przeciwko hipotezie alternatywnej H₁:

H₀ : Y^{^} = f(X₁, X₂,…, X_n)

H₁ : Y^{^} ≠ f(X₁, X₂,…, X_n)

Do weryfikacji posłużymy się testem serii.

Jeśli model budowany jest na podstawie danych dynamicznych szeregujemy reszty według kolejności czasu.

Jeśli model budowany jest na podstawie danych przekrojowych szeregujemy reszty według rosnącej wartości zmiennej objaśniającej. Jeśli jest kilka zmiennych objaśniających to według wybranej zmiennej objaśniającej.

Dla uporządkowanego ciągu reszt obliczamy ilość serii. Serią nazywamy podciąg reszt o tym samym znaku.

Z tablic statystycznych testu liczby serii dla n₁ liczby reszt dodatnich, n₂ liczby reszt ujemnych oraz przyjętego poziomu istotności γ (γ /2 dla test lewostronnego, (1 - γ /2) dla test u prawostronnego) odczytujemy wartości krytyczne S^*₁ , S^*₂ określający zbiór wartości krytycznych.

Jeśli S^*₁ < S < S^*₂ to nie ma podstaw do odrzucenia hipotezy H₀. W przeciwnym razie odrzucamy hipotezę H₀ rozkład odchyleń uznajemy za nielosowy i uznajemy, że postać modelu została źle dobrana.

Przykład (P26 Nowak)

Produkcja przedsiębiorstwa w tys. sztuk (X) w latach 1960-1982 podana jest w poniższej tabeli. Zbudowany został model trendu liniowego oraz oszacowane parametry:

x^{^} = 172 + 3,04 · t

t	xt	x^^t	et
1	158	175,04	-17,04
2	163	178,08	-15,08
3	176	181,12	-5,12
4	185	184,16	0,84
5	188	187,20	0,80
6	198	190,24	7,76
7	199	193,28	5,72
8	201	196,32	4,68
9	205	199,36	5,64
10	211	202,40	8,60
11	216	205,44	10,56
12	214	208,48	5,52
13	215	211,52	3,48
14	220	214,56	5,44
15	223	217,60	5,40
16	224	220,64	3,36
17	223	223,68	-0,68
18	224	226,72	-2,72
19	226	229,76	-3,76
20	230	232,80	-2,80
21	229	235,84	-6,84
22	233	238,88	-5,88
23	234	241,92	-7,92

Na poziomie istotności γ = 0,10 zweryfikować hipotezę o liniowości modelu tendencji rozwojowej produkcji:

H₀ : X^{^} = a₀ + a₁ · t ;

H₁ : X^{^} ≠ a₀ + a₁ · t ;

Obliczamy reszty e_t.

Wyznaczamy ilość serii. Są trzy serie S = 3.

Dla danych n₁ = 10 ; n₂ = 13 (n₁ = 13 ; n₂ = 10) ; γ = 0,05 ; (1-γ = 0,95 odnajdujemy w tablicach serii wartości krytyczne:

S^*₁ = 8 ; S^*₂ = 16 .

Ponieważ S = 3 < S^*₁ = 8 odrzucamy hipotezę H₀ o liniowości trendu.

Decydujemy się na zmianę postaci analitycznej modelu tendencji rozwojowej (trendu). Budujemy model trendu logarytmicznego. Po oszacowaniu parametrów dostajemy model:

x^{^} = 149,73 + 60,3 · log(t)

t	xt	x^^t	et
1	158	149,73	8,27
2	163	167,88	-4,88
3	176	178,50	-2,50
4	185	186,03	-1,03
5	188	191,88	-3,88
6	198	196,65	1,35
7	199	200,69	-1,69
8	201	204,19	-3,19
9	205	207,27	-2,27
10	211	210,03	0,97
11	216	212,53	3,47
12	214	214,80	-0,80
13	215	216,90	-1,90
14	220	218,84	1,16
15	223	220,65	2,35
16	224	222,34	1,66
17	223	223,93	-0,93
18	224	225,42	-1,42
19	226	226,84	-0,84
20	230	228,18	1,82
21	229	229,46	-0,46
22	233	230,68	2,32
23	234	231,84	2,16

Na poziomie istotności γ = 0,10 weryfikujemy hipotezę o logarytmicznym modelu tendencji rozwojowej produkcji:

H₀ : X^{^} = a₀ + a₁ · log(t) ;

H₁ : X^{^} ≠ a₀ + a₁ · log(t) ;

Obliczamy reszty e_t.

Wyznaczamy ilość serii. Jest jedenaście serii S = 11.

Dla danych n₁ = 10 ; n₂ = 13 (n₁ = 13 ; n₂ = 10) ; γ = 0,05 ; (1-γ = 0,95 odnajdujemy w tablicach serii wartości krytyczne:

S^*₁ = 8 ; S^*₂ = 16 .

Ponieważ S^*₁ = 8 < S = 11 < S^*₂ = 16 nie ma podstaw do odrzucenia hipotezy H₀ o logarytmicznej postaci trendu.

Wykład 9

Analiza przepływów międzygałęziowych

Analiza przepływów międzygałęziowych (PM) to rodzaj rachunku makroekonomicznego związanego z badaniem złożonych struktur ekonomicznych. Punktem wyjścia jest bilans gospodarczy w postaci umożliwiającej ilościowe ujęcie zależności między elementami tych struktur. Analizę PM nazywa się również analizą nakładów i wyników lub analizą input-output.

Twórcą analizy przepływów międzygałęziowych jest Wasily Leontieff (początki lat 30 XXw). Za prace związane z PM dostał w 1973 roku nagrodę Nobla z ekonomii.

Uproszczona tablica przepływów międzygałęziowych (TPM)

Sfery produkcji materialnej (produkcja dóbr i usług materialnych).

Dla systemu zamkniętego (bez import, exportu, amortyzacji).

i	Xi	xij				Yi
				1	2		…	n
1	X1	x11	x12	…	x1n	Y1
2	X2	x21	x22	…	x2n	Y2
…	…	…	…	…	…	…
n	Xn	xn1	xn2	…	xnn	Yn
	x0j	x01	x02	…	x0n
	Zj	Z1	Z2	…	Zn
	Xj	X1	X2	…	Xn

Zakładamy, że występuje n gałęzi gospodarki. Przyjmujemy oznaczenia, i, j = 1, 2, 3, … n :

X_i - wartość produktu globalnego i-tej gałęzi gospodarki ;

x_ij - przepływ z gałęzi i do gałęzi j ;

Y_i - wartość produktu finalnego gałęzi i-tej ;

x_0i - płace gałęzi i-tej ;

Z_i - zysk gałęzi i-tej ;

D_i - wartość dodana gałęzi i-tej .

Zachodzą następujące zależności:

x_i1 + x_i2 + … + x_in - to zużycie produkcyjne wyrobów gałęzi i-tej ;

Y_i - to produkt końcowy: eksport, na konsumpcja, inwestycje… ;

Produkt końcowy odpowiada wartości popytu końcowego.

Zużycie produkcyjne odpowiada wartości popytu pośredniego.

Wiersz i-ty odpowiada działalności i-tej gałęzi jako producenta. Bilans działalności i-tej gałęzi ma postać równania podziału:

X_i = x_i1 + x_i2 + … + x_in + Y_i ;

Kolumny w tabeli opisują proces produkcji, wartości produktów zużywanych przez daną gałąź. Suma przepływów do j-tej gałęzi, to koszt poniesiony przez gałąź na zakup towarów potrzebnych do jej procesu produkcyjnego. Ta suma to KM_j - koszty materiałowe:

KM_j = x_1j + x_2j + … + x_nj ;

Koszty materiałowe KM_j wraz z płacami x_0j dają K_j łączny koszt produkcji:

K_j = x_0j + KM_j ;

Różnica między wartością wielkością produkcji globalnej, a poniesionymi kosztami to zysk danej gałęzi:

Z_j = X_j - K_j ;

Wartością dodaną D_j w j-tej gałęzi produkcji nazywaną też produkcją czystą, jest różnica między wartością produkcji globalnej, a kosztami materiałowymi.

Tak więc wartość dodana to płace i zysk:

D_j = X_j - (x_1j + x_2j + … + x_nj) = x_0j + Z_j ;

Kolumny w tabeli przepływów międzygałęziowych opisują bilans kosztów i zysków gałęzi, co możemy zapisać równaniem kosztów dla j-tej gałęzi. Suma wszystkich składników w kolumnie daje wartość produktu globalnego danej gałęzi. Równanie to nazywamy równaniem kosztów:

X_j = x_0j + x_1j + x_2j + … + x_nj + Z_j ;

Łączną produkcję globalną całego systemu możemy obliczyć na podstawie gałęziowych bilansów podziału:

Możemy też obliczyć na podstawie gałęziowych bilansów kosztów:

Skąd dostajemy równanie wiążące płace i zyski z produktem finalnym:

Gdy tabela przepływów międzygałęziowych opisuje całą gospodarkę, ostatnie równanie jest warunkiem równowagi ogólnej. Strony równania opisują produkt krajowy (lub dochód narodowy). Jedna strona równania (lewa) to opis podażowy (rzeczowy). Druga strona (prawa) t opis popytowy (pieniężny).

Lewa strona (podażowa) odnosi się do wyprodukowanych towarów lecz jest wyrażona wartościowo w określonych cenach. Zmiana cen, przy niezmienionej wielkości rzeczowej, zmienia wartość lewej strony równania.

Prawa strona określa środki pieniężne: wynagrodzenia, podatki, dywidendy, fundusze przeznaczone na rozwój przedsiębiorstw. Zmiana poziomu płac lub podatków zmienia prawą stronę równania.

Jak widać zmiana jednej ze stron równania narusza równowagę i w rezultacie powoduje zmiany po drugiej stronie równania (np. zmiany inflacyjne).

Przykład 1 (dane z przykładu 13.1 Ekonometria SGH)

Trójgałęziowy system gospodarczy.

i	Xi		xij		Yi
1	500	50	195	0	255
2	300	100	0	90	110
3	150	80	45	15	10
	x0j	200	30	15
	Zj	70	30	30
	Xj	500	300	150

Bilans podziału produkcji globalnej gałęzi 1:

500 = 50 + 195 + 0 + 255

Bilans kosztów w gałęzi 2:

300 = 195 + 0 + 45 + 30 + 30

Czy spełniony jest warunek równowagi?

255 + 110 + 10 = 200 + 70 + 30 + 30 + 15 + 30

Tak warunek równowagi jest spełniony.

Rozpatrzmy teraz tabelę przepływów międzygałęziowych dla systemu otwartego. Uwzględniamy w tabeli import, export, amortyzację. Oraz uwzględniając podział produktu finalnego zgodnie z jego przeznaczeniem: spożycie, inwestycje brutto, przyrost środków obrotowych i rezerw, eksport.

i

Xi

xij

Yi

1

2

…

n

Spożycie (1)

Inwestycje (2)

śr.obrot rez. (2)

Eksport (4)

1

X1

x11

x12

…

x1n

Y1^(1)

Y1^(2)

Y1^(3)

Y1^(4)

2

X2

x21

x22

…

x2n

Y2^(1)

Y2^(2)

Y2^(3)

Y2^(4)

…

…

…

…

…

…

…

…

…

n

Xn

xn1

xn2

…

xnn

Yn^(1)

Yn^(2)

Yn^(3)

Yn^(4)

n+1

import

xn+1,1

xn+1,2

…

xn+1,n

xn+1^(1)

xn+1^(2)

xn+1^(3)

xn+1^(4)

n+2

amortyz.

xn+2,1

xn+2,2

…

xn+2,n

x01

x02

…

x0n

Z1

Z2

…

Zn

X1

X2

…

Xn

Koszty materialne KMA_j dla gałęzi j-tej to koszty materiałowe krajowe i importowe oraz amortyzacja.

KMA_j = x_1j + x_2j + … + x_nj + x_n+1,j + x_n+2,j ;

Zaś koszt ogólny produkcji uwzględniający płace to K_j :

K_j = x_0j + x_1j + x_2j + … + x_nj + x_n+1,j + x_n+2,j ;

Zysk jest różnicą między wartością wytworzoną produkcji globalnej, a poniesionymi kosztami:

Z_j = X_j - K_j = X_j - (x_0j + x_1j + x_2j + … + x_nj + x_n+1,j + x_n+2,j)

Wartość dodana (produkcja czysta) to różnica między wartością produkcji globalnej a kosztami materialnymi, czyli :

D_j = X_j - (x_1j + x_2j + … + x_nj + x_n+1,j + x_n+2,j) = x_0j + Z_j ;

Równanie kosztów (kolumna) dla j-tej gałęzi ma postać:

X_j = x_0j + x_1j + x_2j + … + x_nj + x_n+1,j + x_n+2,j + Z_j ;

Zaś równanie podziału produkcji (wiersz) dla i-tej gałęzi ma postać:

X_i = x_i1 + x_i2 + … + x_in + Y_i⁽¹⁾ + Y_i⁽²⁾ + Y_i⁽³⁾ + Y_i⁽⁴⁾ ;

Warunek równowagi systemu ma więc postać:

lub postać:

(*)

Dochód narodowy, produkt krajowy

Jeśli analiza przepływów międzygałęziowych dotyczy całej gospodarki to równanie (*) pozwala nam wnioskować o głównych miernikach działalności gospodarczej w skali makro.

Obie strony równania ukazują wartość dochodu narodowego wytworzonego brutto: lewa strona kierunki zużycia, prawa źródła powstania.

Przyjmijmy oznaczenia:

DN - dochód narodowy ;

P - podzielony (do dyspozycji) ;

W - wytworzony ;

B - brutto ;

N - netto ;

AM - amortyzacja -

SHZ - saldo handlu zagranicznego

Posługując się równaniem (*) na podstawie tabeli przepływów międzygałęziowych możemy obliczyć dochód narodowy wytworzony brutto:

czyli dochód narodowy wytworzony brutto może być liczony jako suma: wartości dodanej (produkcji czystej) w gałęziach produkcji materiałowej oraz amortyzacji środków trwałych.

Uwzględniając znane z ekonomii zależności:

DNB = DNN + AM

DNP = DNW - SHZ

DNWB = DNWN + AM

Otrzymujemy:

czyli dochód narodowy wytworzony netto może być liczony jako wartość dodana (produkcja czysta) w gałęziach produkcji materiałowej.

A ponieważ

DNPB = DNWB - SHZ =

z równania (*) dostajemy

Czyli dochód narodowy podzielony (do dyspozycji) możemy obliczać ze wzorów:

(a)

Oraz

(b)

Wniosek:

Dochód narodowy wytworzony brutto to suma wartości dodanej (produkcji czystej) w gałęziach produkcji materialnej i amortyzacji.

Dochód narodowy wytworzony (netto) to suma wartości dodanej (produkcji czystej) w gałęziach produkcji materialnej (bez amortyzacji).

Dochód narodowy podzielony (do dyspozycji) to dochód narodowy wytworzony skorygowany o saldo obrotów z zagranicą.

Wzory (a) i (b) pokazują strukturę podziału dochodu narodowego, składniki popytu końcowego: krajowe i importowane dobra konsumpcyjne, inwestycyjne, przeznaczone na zwiększenie środków obrotowych, rezerw. Przy dochodzie brutto inwestycje obejmują wartość odtworzenia środków trwałych (inwestycje brutto). Przy dochodzie netto, od wartości inwestycji odliczana jest amortyzacja (inwestycje netto).

Przedstawione mierniki: produkt globalny i dochód narodowy do lat 90 były podstawowymi miernikami działalności gospodarczej stosowanymi w Polsce. Obliczenia prowadzono na podstawie danych dotyczących produkcji jednostek gospodarki narodowej zaliczonych do sfery materialnej, według systemu Material Product System (MSP).

Przykład 2 (dane z przykładu 13.2 Ekonometria SGH)

W statystycznych danych zbiorczy często pojawia się rubryka „sumy niezbilansowane”. W obliczeniach musimy je uwzględnić.

Bilans dla tradycyjnego podziału n=7 działów produkcji materialnej: 1-przemysł, 2-budownictwo, 3-rolnictwo, 4-leśnictwio, 5-transport i łączność, 6-handel, 7-pozostałe gałęzie produkcji materialnej i gospodarka komunalna.

Dane w bilionach zł. cenach bieżących, zaokrąglone do 3 miejsc po przecinku. Dane zblokowane. Dodatkowo wiersz i kolumna sum niezbilansowanych, obliczone przez agregację danych indywidualnych.

Tabela przepływów międzygałęziowych gospodarki Polski w roku 1989 (GUS) mln zł

i	Xi	xij	sumy niezbilansowane	Yi spożycie	Yi inwestycje	Yi śr.obrot. rezerwy	Yi eksport
1
	197,549	80,813	-1,385	54,092	17,010	25,270	21,749
n
	sumy niezbilansowane	-0,761
	import	10,294		3,077	2,341	0,912	0,834
	amortyzacja	2,252
	x0j	47,328
	Zj	57,623
	Xj	197,549

Na podstawie tabeli obliczyć produkt globalny w Polsce w roku 1989.

Licząc metodą gałęziowych bilansów podziału (sumując w wierszach) dostajemy

X₁ + … + X_n = 80,813 - 1,385 + +54,092 + 17,010 + 25,270 + 21,749 = 197,549

Licząc metodą gałęziowych bilansów kosztów (sumując w kolumnach) dostajemy :

X₁ + … + X_n = 80,813 - 0,761 + 10,294 + 2,252 + 47,328 + 57,623 + 197,549 = 197,549

DNWB = DNWN + AM = 104,951 + 2,252 = 107,203

DNPB = DNWB - SHZ =
= 54,092 + 17,01 + 25,27 + 3,077 + 2,341 + 0,912 = 102,702

= 102,702 - 2,252 = 100,450

Równość:

DNW = DNP + SHZ

jest spełniona z dokładnością do sum niezbilansowanych:

DNW = 104,951

DNP = 100,450

SHZ = 21,749 - (10,294 +3,077 + 2,341 + 0,912) = 5,125

104,951 - 0,761 = 100,450 + 5,125 - 1,385.

Wykład 10

Analiza przepływów międzygałęziowych (cd)

Produkt globalny i dochód narodowy były podstawowymi miernikami działalności gospodarczej w Polsce do początku lat 90. Obliczenia prowadzono według systemu MPS (Material Product System) uwzględniającego produkcję jednostek gospodarki narodowej zaliczonych do sfery produkcji materialnej. Obecnie uwzględnia się również mierniki wartość globalną i produkt krajowy (brutto, netto) liczone według systemu SNA (System of National Accounts).

Wartość globalna (WG) to całkowita wartość dóbr i usług wytworzonych w ciągu roku w gospodarce (nie tylko dóbr materialnych). Wartość globalna to produkt globalny powiększony o wartość wytworzonych usług i innych dóbr niematerialnych.

Czyli zachodzi równanie:

WG = PG + WGU

(Wartość globalna) = (Produkt globalny) + (Wartość globalna usług niematerialnych)

Gdzie WGU to wartość globalna usług niematerialnych.

Produkt krajowy brutto (PKB) to wartość globalna pomniejszona o wartości zużycia pośredniego materialnego i niematerialnego.

PKB = DNWB + WGU - W₁ - W₂

Gdzie:

PKB - Produkt krajowy brutto

DNWB - Dochód narodowy wytworzony brutto

WGU - Wartość globalna usług niematerialnych

W₁ - Wartość usług niematerialnych zużytych w sferze materialnej

W₂ - Wartość wyrobów i usług zużytych poza sferą materialną

Produkt krajowy netto to produkt krajowy brutto pomniejszony o amortyzację.

Produkt narodowy brutto (PNB) to wartość PKB zmodyfikowana o saldo dochodów przekazanych za granicę i otrzymanych z zagranicy z tytułu działalności gospodarczej.

Związki między systemem rachunków MPS i SNA ilustruje poniższa tabela:

	Zużycie pośrednie w sferze produkcji		Zużycie końcowe
	dóbr i usług materialnych	usług niematerialnych
Produkcja dóbr i usług materialnych	A	B	C
Produkcja usług niematerialnych	D	E	F

Zachodzą związki:

PG = A + B + C (MPS)

WGU = D + E + F (rachunek SNA)

WG = PG + WGU = A + B + C + D + E + F (liczone wg SNA)

W₁ = D ; W₂ = B + E (rachunek SNA)

Widzimy więc, że pierwszy wiersz powyższej tabeli (bloki A, B, C) to schematyczny odpowiednik TPM czyli tabeli przepływów międzygałęziowych. Blok A to odpowiednik macierzy X TPM, zaś B i C to odpowiednik wektora Y produktu końcowego.

Tak więc:

DNWB = B + C (rachunek MPS)

PKB = C + F (rachunek SNA)

Skąd:

PKB = DNWB + F - B

Wyznaczając:

F - B = D+E+F -D -(B+E) = WGU -D -(B+E) = WGU - W₁ -W₂

Dostajemy:

PKB = DNWB + WGU - W₁ - W₂

Przykład 1 (kontynuacja przykładu 2 z wykładu 9) (dane z przykładu 13.2, 13.3 Ekonometria SGH)

(Rocznik statystyczny 1992, wartości dla roku 1989)

Dane z przykładu 2 wykład 6 uzupełniamy tabelą gdzie brakujące dane są uzupełnione na podstawie Rocznika Statystycznego 1992:

WGU = 22,842 (wartość globalna usług niematerialnych)

W₁ = 2,934 (usługi niematerialne zużyte w sferze materialnej)

W₂ = 2,158 + 6,635 = 8,793 (łączna wartość usług i wyrobów zużytych poza sferą materialną)

	Zużycie pośrednie w sferze produkcji		Zużycie końcowe
	dóbr i usług materialnych	usług niematerialnych
Produkcja dóbr i usług materialnych	A = 90,346	B = 6,635	C = 100,568
Produkcja usług niematerialnych	D = 2,934	E = 2,158	F = 17,750

Obliczyć WG wartość globalną i PKB produkt krajowy brutto dla roku 1989

WG = PG + WGU = 197,549 + 22,842 = 220,391

PKB = DNWB + WGU - W₁ - W₂ = (6,635 + 100,568) + 22,842 - 2,934 - 8,793 = 118,318

Wskaźniki efektywności działalności gospodarczej

Tablica przepływów międzygałęziowych (TMP) umożliwia policzenie niektórych syntetycznych współczynników charakteryzujących procesy produkcji zarówno w gałęziach produkcji jak i w całym systemie gospodarczym.

Współczynnik materiałochłonności m_j produkcji globalnej w j-tej gałęzi produkcji (koszty materiałowe do produktu globalnego):

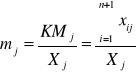
Współczynnik materiałochłonności m produkcji globalnej dla całej gospodarki:

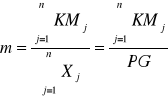
Współczynnik importochłonności imp_j j-tej gałęzi produkcji (materiały importowane do produktu globalnego):

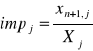
Współczynnik importochłonności imp produkcji dla całej gospodarki:

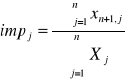
Współczynnik rentowności produkcji r_j j-tej gałęzi produkcji:

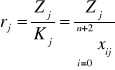
W publikacjach statystycznych TPM, czyli tablica przepływów międzygałęziowych często uzupełniana jest informacjami dotyczącymi zatrudnienia i wartości produkcyjnego majątku trwałego w poszczególnych gałęziach.

Przyjmijmy oznaczenia:

L_j - liczba pracowników zatrudnionych w j-tej gałęzi ;

ST_j - wartość produkcyjnych środków trwałych w j-tej gałęzi.

Możemy określić następujące współczynniki:

Pracochłonność produkcji j-tej gałęzi =

Wydajność pracy w j-tej gałęzi =

Majątkochłonność produkcji j-tej gałęzi =

Produktywność majątku trwałego w j-tej gałęzi =

Techniczne uzbrojenie pracy w j-tej gałęzi =

		xij
i	Xi	1	2	3	4	razem
1	255	30	0	58	30	118
2	340	50	40	45	0	135
3	285	25	50	60	30	165
4	195	20	30	0	40	90
5	import	24	35	30	10	99
6	amort.	25	42	28	15	110
	płace	55	120	45	52	272
	zysk	26	23	19	18	86
	Xj	255	340	285	195	1075
	Lj	8,2	9,5	10,2	12,5	40,4
	STj	83	92	105	80	360
		xij
i		1	2	3	4	razem
1	materiałochłonność	0,584	0,456	0,677	0,564	0,565
2	Rentowność	0,114	0,073	0,071	0,102	0,087
3	Importochłonność	0,094	0,103	0,105	0,051	0,092
4	Majątkochłonność	0,325	0,271	0,368	0,410	0,335
5	Produktywność środków trwałych	3,072	3,696	2,714	2,438	2,986
6	Pracochłonność	0,032	0,028	0,036	0,064	0,038
	Techniczne uzbrojenie pracy	10,122	9,684	10,294	6,400	8,911
	Wydajność pracy	31,098	35,789	27,941	15,600	26,609

Wykład 11

Model Leontiefa

Tablica przepływów międzygałęziowych Leontiefa pozwala opisać procesy wytwórcze za pomocą relacji między nakładami (kolumny), a wynikami (wiersze) dla poszczególnych gałęzi systemu gospodarczego (relacje input-output). Założenie modelu - te relacje są stałe w czasie.

Na podstawie TPM budujemy macierz A = [a_ij]_nxn zwaną macierzą struktury kosztów.

Niech a_ij i-ty współczynnik kosztów dla j-tej gałęzi:

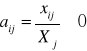
i,j = 1, 2,… n.

a_ij nazywamy również współczynnikiem bezpośredniej materiałochłonności.

Suma współczynników a_ij w kolumnie równa jest współczynnikowi m_j materiałochłonności dla j-tej gałęzi:

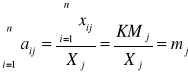
gdzie: KM_j to koszty materiałowe. Będziemy zakładać, że m_j < 1.

Przykład 1 (cd przykładu 1 wykład 9) macierz struktury kosztów A:

a11 = 50/500 = 0,1	a12 = 195/300 = 0,65	a13 = 0/150 = 0
a21 = 100/500 = 0,2	a22 = 0/300 = 0	a23 = 90/150 = 0,6
a31 = 80/500 = 0,16	a32 = 45/300 = 0,15	a33 = 15/150 = 0,1

Współczynniki materiałochłonności wynoszą odpowiednio:

m₁ = 0,1+0,2+0,16 = 0,46; m₂ = 0,65+0+0,15 = 0,8; m₃ = 0+0,6+0,1 = 0,7.

Macierz struktury kosztów A oraz współczynników kosztów a_ij używana jest do opisania zależności między produkcją globalną i produkcją końcową.

Równania podziału:

X₁ = x₁₁ + x₁₂ +…+ x_1n + Y₁ ;

X₂ = x₂₁ + x₂₂ +…+ x_2n + Y₂ ;

……

X_n = x_n1 + x_n2 +…+ x_nn + Y_n ;

Wykorzystując zależność x_ij = a_ijX_j , w równaniach podziału dostajemy:

X₁ = a₁₁X₁ + a₁₂X₂ +…+ a_1nX_n + Y₁ ;

X₂ = a₂₁X₁ + a₂₂X₂ +…+ a_2nX_n + Y₂ ;

……

X_n = a_n1X₁ + a_n2X₂ +…+ a_nnX_n + Y_n ;

Przenosząc wszystkie wyrażenia z X na lewą stronę dostajemy:

X₁ - a₁₁X₁ - a₁₂X₂ -…- a_1nX_n = Y₁ ;

X₂ - a₂₁X₁ - a₂₂X₂ -…- a_2nX_n = Y₂ ;

……

X_n - a_n1X₁ - a_n2X₂ -…- a_nnX_n = Y_n ;

Po uporządkowaniu względem indeksu X_j :

(1 - a₁₁)X₁ - a₁₂X₂ -…- a_1nX_n = Y₁ ;

- a₂₁X₁ + (1- a₂₂)X₂ -…- a_2nX_n = Y₂ ;

……

- a_n1X₁ - a_n2X₂ -…+ (1- a_nn)X_n = Y_n ;

I w postaci macierzowej:

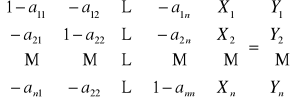
oraz równoważnie:

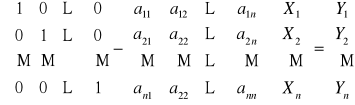
czyli:

(I - A)X = Y

Powyższe równanie nazywamy modelem Leontiefa. Macierz (I-A) nazywamy macierzą Leontiefa.

gdzie:

I - macierz jednostkowa (nxn);

A - macierz struktury kosztów (nxn);

X - wektor produkcji globalnej (n);

Y - wektor produkcji finalnej (n).

Model Leontiefa służy do określania wielkości produkcji finalnej, dla ustalonej produkcji globalnej lub określania produkcji globalnej koniecznej do osiągnięcia wymaganej produkcji finalnej.

Model Leontiefa jest jednorodny i addytywny:

1. jednorodność: (I-A) aX = a(I-A) X = aY

2. addytywność: (I-A) (X^' + X^'') = (I-A)X^' + (I-A)X^'' = Y^' + Y^''

Wniosek

Do obliczenia przyrostu produktu finalnego wynikającego z danego przyrostu produktu globalnego, wystarczy znajomość samego przyrostu produktu globalnego.

Istotnie:

(I-A) (X + X) = (I-A)X + (I-A) X = Y + Y,

skąd:

(I-A) X = Y,

Model Leontiefa pozwala więc łatwo wnioskować o skutkach względnej lub absolutnej zmiany produktu globalnego.

Przykład 2 (cd przykładu 1) Wyznaczenie macierzy Leontiefa

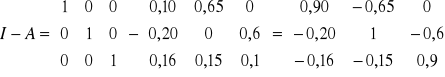
Przykład 3 (cd przykładu 1) Wyznaczenie produktu finalnego dla danego produktu globalnego.

Niech X^T = [500 300 150]

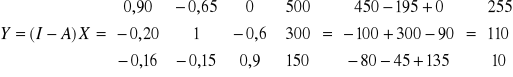
Wynik jest zgodny z danymi z przykładu 1 wykład 9.

Przykład 4 (cd przykładu 1)

O ile wzrośnie produkt finalny jeśli wiadomo, że produkt globalny w każdej gałęzi wzrośnie o 5%?

X^'T = 1,05·X^T = 1,05 [500 300 150] = [525 315 157,5]

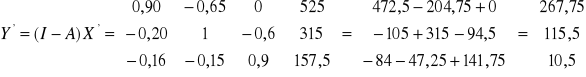
Y^'T = 1,05·Y^T = 1,05 [255 110 10] = [267,8 115,5 10,5]

Przykład 5 (cd przykładu 1)

O ile wzrośnie produkt finalny jeśli wiadomo, że produkt globalny X zmieni się o X?

X^T = [50 20 -10]

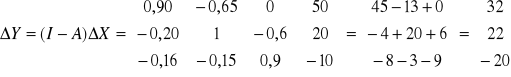
Ekonomiczna interpretacja a_ij elementów macierzy Leontiefa.

Niech X^T = [0 … 0 1 0 … 0] przyrost o jednostkę na j-tym miejscu, to

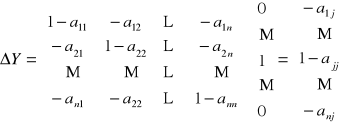
Przyrost produktu finalnego Y w tym przypadku jest równy j-tej kolumnie macierzy Leontiefa (I-A).

Jednostkowy przyrost j-tego produktu globalnego, powoduje zmianę produktu finalnego we wszystkich gałęziach. Zmiana w I-tej gałęzi jest równa i-temu elementowi j-tej kolumny macierzy Leontiefa (I-A). Czyli dla i≠j wzrost produkcji globalnej w gałęzi j powoduje spadek produktu finalnego gałęzi i o wielkość a_ij oraz wzrost produktu finalnego w gałęzi j o wielkość (1-a_jj).

Przykład 6 (cd przykładu 1)

Jaka zmiana w produkcji finalnej nastąpi w wyniku jednostkowego zwiększenia produkcji globalnej w gałęzi 3.

Odpowiedź:

Trzecia kolumna opisuje odpowiednią zmianę produkcji:

1. Produkt finalny gałęzi 1 będzie bez zmian;

2. Produkt finalny gałęzi 2 zmniejszy się o 0,6;

3. Produkt finalny gałęzi 3 zwiększy się o 0,9.

Uwaga

Założyliśmy, że:

1. a_ij ≥ 0 dla każdego i, j;

2. suma a_ij po i, czy suma w kolumnie macierzy A, jest mniejsza od 1;

Te założenia gwarantują odwracalność macierzy Leontiefa (I-A) czyli istnienie macierzy (I-A)^-1. Mnożąc lewostronnie

(I - A)X = Y

przez (I-A)^-1 dostajemy:

(I-A)^-1(I-A)X = (I-A)^-1Y

Skąd:

(I-A)^-1Y = X.

czyli postać modelu Leontiefa pozwalającego określać wektor produkcji globalnej na podstawie produkcji finalnej.

Ta postać modelu Leontiefa jest również jednorodna i addytywna względem produkcji finalnej:

1. jednorodność: (I-A)^-1 aY = a(I-A)^-1 Y = aX

2. addytywność: (I-A)^-1 (Y^' + Y^'') = (I-A)^-1 Y^' + (I-A)^-1 Y^'' = X^' + X^''

Wniosek

(I-A)^-1 Y = X,

Przykład 7 (cd przykładu 1)

Obliczyć macierz odwrotną do macierzy Leontiefa

=

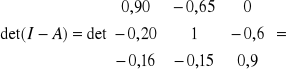
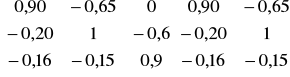
= 0,81 - 0,0624 - 0,081 -0,117 = 0,5496 = det(I-A)

Mając obliczony wyznacznik liczymy macierz odwrotną:

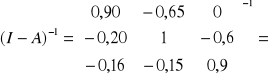
	+[1·0,9-(-0,6)(-0,15)]	-[(-0,65) ·0,9-0·(-0,15)]	+[(-0,65)(-0,6)-0·(-1)]
=1/0,5496	-[(-0,2)·0,9-(-0,6)(-0,16)]	+[0,9·0,9-0·(-0,16)]	-[0,9·(-0,6)-0·(-0,2)]
	+[(-0,2)(-0,15)-1·(-0,16)]	-[(-0,2)(-0,15)-1·(-0,16)]	+[0,9·1-(-0,65)(-0,2)]

	0,81	0,585	0,39
=1/0,5496	0,276	0,81	0,54
	0,19	0,239	0,77

	1,474	1,064	0,710
(I-A)^-1 =	0,502	1,474	0,983
	0,346	0,435	1,401

Przykład 7 (cd przykładu 1)

Obliczmy wielkość produkcji globalnej X przy której wektor produkcji finalnej Y^T = [255 110 10].

	1,47	1,06	0,71		255		500
X=(I-A)^-1Y=	0,50	1,47	0,98		110	=	300
	0,35	0,43	1,40		10		150

	1,47·255+1,06·110+0,71·10		500
=	0,5·255+1,47·110+0,98·10	=	300
	0,35·255+0,43·110+1,4·10		150

A więc jest zgodność z danymi początkowymi.

Przykład 8 (cd przykładu 1)

O ile musi zwiększyć się produkt globalny by produkt finalny zwiększył się o 7%.

Odpowiedź

Z jednorodności modelu Leontiefa, wiemy, że produkt globalny też musi zwiększyć się o 7%.

Przykład 9 (cd przykładu 1)

Jaka musi być zmiana produktu globalnego by nastąpiła zmiana produktu finalnego o Y^T = [10 -5 0].

Odpowiedź

	1,47	0,50	0,35		10		12,23
X =	1,06	1,47	0,43		-5	=	3,28
	0,71	0,98	1,40		0		2,18

Musi nastąpić wzrost X = [12,33 3,28 2,18].

Ekonomiczna interpretacja macierzy odwrotnej do macierzy Leontiefa (I-A)^-1

Oznaczmy B = [b_ij]_nxn = (I-A)^-1. Macierz B nazywamy macierzą współczynników pełnej materiałochłonności. Elementy b_ij nazywamy współczynnikami pełnej materiałochłonności, b­_ij to wartość o ile musi wzrosnąć j-ty produkt globalny, by i-ty produkt finalny wzrósł o jednostkę przy niezmienionych pozostałych produktach finalnych.

Niech Y^T = [0 … 0 1 0 … 0] przyrost o jednostkę na j-tym miejscu, to

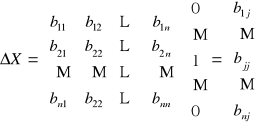
Wektor j-ty określa o ile musi zwiększyć się produkcja globalna, by w j-tej gałęzi nastąpił jednostkowy wzrost produktu finalnego przy niezmienionym produkcie finalnym w pozostałych gałęziach.

Prognozowanie na podstawie modelu Leontiefa.

Na podstawie bilansu przepływów międzygałęziowych wyznaczmy: macierz X, macierz A, macierz (I-A), macierz (I-A)^-1. Zakładamy, że wyznaczone macierze są stałe w rozpatrywanym czasie i będą takie same w okresie na który, wykonywana jest prognoza.

Prognoza I rodzaju.

Na podstawie oceny możliwości wytwórczych systemu ekonomicznego określamy wielkość produktu globalnego X. Przy pomocy modelu Leontiefa prognozujemy wielkość produktu finalnego Y:

Y = (I-A) X

Prognoza II rodzaju.

Na podstawie oceny przyszłego zapotrzebowania na produkt finalny określamy wielkość wektora produktu finalnego Y. Przy pomocy modelu Leontiefa wyznaczamy wielkość wymaganego produktu globalnego X niezbędnego do wyprodukowania wymaganego wektora produkcji finalnej Y:

X = (I-A)^-1 Y

Prognoza mieszana.

Na podstawie oceny przyszłego zapotrzebowania na produkt finalny części gałęzi produkcji oraz na podstawie oceny możliwości wytwórczych pozostałych gałęzi, przy pomocy modelu Leontiefa ustalamy pozostałe wielkości wektorów produkcji globalnej i finalnej.

Przykład 10 (cd przykładu 1)

Zakładamy, że dane z przykładu 1 dotyczyły okresu t. Badamy zachowanie się sytemu gospodarczego w następnym okresie, czyli w okresie (t+1). Na podstawie danych ekonomicznych oceniamy, że produkt globalny w gałęzi 3 nie zmieni się, zaś w gałęziach 1 i 2 wzrośnie o 10%. Jaki będzie produkt finalny w okresie (t+1)?

Rozwiązanie

Produkt globalny w okresie (t+1) wyniesie:

X^T_t+1 = [550 330 150]

Produkt finalny w okresie (t+1) wyniesie:

	0,9	-0,65	0		550,00		280,5
Yt+1 =	-0,2	1	-0,6		330,00	=	130,0
	-0,16	-0,15	0,9		150,00		-2,5

Z wykonanej prognozy I rodzaju wynika, że do zrealizowania zakładanej produkcji globalnej potrzebny jest import produktów gałęzi. Do zaspokojenia popytu pośredniego potrzeba produktów gałęzi 3 o wartości 2,5 jednostki.

Przykład 11 (cd przykładu 1)

Chcemy uniknąć konieczności importu towarów z gałęzi 3. Jaki powinien być wektor produkcji globalnej, tak by wektor produkcji finalnej wynosił:

Y^T_t+1 = [280,5 130,0 0]

Rozwiązanie

Wyznaczamy prognozę II rodzaju dla ustalonego wektora produkcji finalnej:

	1,47	1,06	0,71		280,5		551,77
Xt+1 =	0,50	1,47	0,98		130,0	=	332,46
	0,35	0,43	1,40		0,0		153,50

Unikniemy konieczności importu, jeśli wektor produkcji globalnej X^T_t+1 wyniesie [551,77 332,46 153,50].

Zwiększając produkcję globalną:

działu pierwszego o (551,77 - 500)/500 % = 10,35% zamiast 10%,

działu drugiego o (332,46 - 330)/300 % = 10,82% zamiast 10%,

działu trzeciego o (153 - 150)/150 % = 2,34% zamiast 0%

unikniemy konieczności importu.

Przykład 12 (cd przykładu 1)

Prognoza mieszana na okres (t+1).

Sądzimy, że:

w dziale 3 nie zmieni się produkcja globalna ani popyt końcowy, czyli X₃ = 0, Y₃ = 0;

w dziale 2 zwiększy się popyt końcowy o wartość równą 10 jednostek, czyli Y₂ = 10;

Musimy wyznaczyć pozostałe wielkości: X₁, X₂ , Y₁. Z modelu Leontiefa otrzymujemy układ równań:

(I-A) X = Y

czyli:

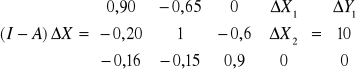
0,9 X₁ -0,65 X₂ = Y₁

-0,2 X₁ + X₂ = 

-0,16 X₁ -0,15 X₂ = 

Skąd dostajemy:

X₁ = ,  X₂ = ,  Y₁ = -12,58 

Tak więc przy poczynionych założeniach sądzimy, że system gospodarczy będzie opisywany wektorami:

X^T_t+1 = [-7,89 8,42 0] ; Y^T_t+1 = [-12,58 10 0].

X^T_t+1 = [492,11 308,42 150] ; Y^T_t+1 = [242,42 120 10].

Ekonometria I Eko II W1

49 / 49

---