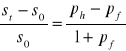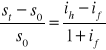Związki kursów walut, stóp procentowych i inflacji
Rozpoznawanie związków między kursami walutowymi a wielkościami ekonomicznymi jest potrzebne do:
prognozowania kursów walutowych
zarządzania ryzykiem walutowym przedsiębiorstwa
Relacje między kursami walutowymi a stopami procentowymi, i cenami na światowych rynkach tłumaczone są przez prawo jednej ceny, które mówi, że takie same lub ekwiwalentne rzeczy powinny miec tę samą cenę na różnych rynkach.
Relacje parytetowe między walutami określają warunki równowagi popytu i podaży na rynku walutowym, w których brak możliwości uzyskiwania zysków arbitrażowych
W warunkach swobody przepływu kapitałów i towarów zmiany kursów walut powodowane są wyrównywaniem się
relacji między stopami inflacji a stopami procentowymi
relacji między kasowymi a terminowymi kursami walutowymi
Gdy prawo jednej ceny nie obowiązuje można uzyskiwać dochody arbitrażowe.
Arbitraż polega na równoczesnym zakupie i sprzedaży identycznych lub ekwiwalentnych aktywów w celu uzyskania gwarantowanego zysku
Parytet siły nabywczej
Ogólna teoria parytetu siły nabywczej (purchasing power parity PPP)
Teoria ta zakłada, że poziom kursu walutowego powinien być taki, żeby ceny standardowego koszyka produktów w różnych krajach były takie same
tj. innymi słowy zakłada się, że za jednego dolara USA można kupić taką samą ilość dóbr w USA, Wlk.Brytanii, Chinach i Polsce
warunkiem funkcjonowania PPP jest wolność handlu i pominięcie kosztów transportu
tygodnik `The Economist' oblicza wskaźnik o nazwie `Big Mac PPP' tj. kursy wymiany, które zrównałyby cenę Big Mac'ów w McDonaldach na całym świecie
![]()
gdzie
s - kurs wymiany tj. wartość jednostki waluty zagranicznej wyrażonej w walucie krajowej
Πh - poziom cen krajowych
Πf - poziom cen zagranicznych
Czyli jeśli cena standardowego koszyka produktów wynosi 465 złotych w Polsce i 100 Euro w krajach strefy Euro to kurs wymiany wyniesie 4,65 EUR/PLN
![]()
Jeśli poziom cen nie będzie równy to nastąpi arbitraż handlowy i kraje mające wyższy poziom cen będą importować z krajów mających niższy poziom cen póki kurs walutowy będzie czynił to opłacalnym
Względna teoria parytetu siły nabywczej
Ta wersja teorii parytetu siły nabywczej mówi, że zmiana kursu wymiany odpowiada zmianom w poziomach cen w kraju i zagranicą tj. stopom inflacji
Analogicznie do zależności ogólnej teorii parytetu siły nabywczej
![]()
zależność tę można przedstawić jako
![]()
gdzie :
s0 - wartość jednostki waluty zagranicznej wyrażonej w walucie krajowej na początek danego okresu
st - wartość jednostki waluty zagranicznej wyrażonej w walucie krajowej na koniec danego okresu
e - stopa zmiany poziomu kursu walutowego czyli stopa deprecjacji lub aprecjacji
ph - stopa inflacji w kraju
pf - stopa inflacji za granicą
1+ph - nowy poziom cen krajowych
1+pf - nowy poziom cen zagranicznych
Względna teoria parytetu siły nabywczej c.d.
Względną teorię parytetu siły nabywczej można stosować dla prognozowania przyszłego kursu walutowego na podstawie przewidywanych stóp inflacji oraz bieżącego kursu walutowego
Np. jeśli inflacja w Polsce jest wyższa niż w USA to kurs walutowy złotego musi spaść w stosunku do dolara odpowiednio do różnicy w stopach inflacji
Przykład
Inflacja w Polsce 2%
Inflacja w USA 1%
Kurs bieżący dolara 3,8200
Kurs przyszły
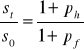
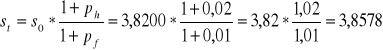
Wniosek:
Ponieważ inflacja w Polsce jest wyższa niż w USA to kurs walutowy złotego powinien się osłabić względem dolara
Względna teoria parytetu siły nabywczej c.d.
![]()
Po przekształceniu
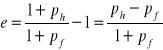
jako, że stopa deprecjacji/aprecjacji kursu waluty zagranicznej wynosi
![]()
to podstawiając do powyższego wzoru otrzymujemy
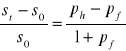
Ze względnej teorii siły nabywczej wynika, że aby pozycja konkurencyjna kraju się nie pogorszyła zmiany kursu walutowego muszą kompensować zmiany cen towarów
Jeśli w kraju jest inflacja większa niż za granicą to kurs waluty krajowej musi się osłabić.
Jeśli w kraju jest inflacja mniejsza niż z granicą to kurs waluty musi się wzmocnić
Weryfikacja zasady parytetu siły nabywczej w rzeczywistości
Większość badań odrzuca tę zasadę
wynika to z istnienia znacznych barier w handlu międzynarodowym, które uniemożliwiają skuteczny arbitraż
część obrotów na rynku to usługi, które w większości z natury rzeczy nie podlegają swobodnej wymianie międzynarodowej
zmiany cen w granicach kosztów transportu nie wpływają na działania dostosowawcze kursu
zasada parytetu siły nabywczej była zauważalna w krajach Unii Europejskiej
Czemu więc służy zasada parytetu siły nabywczej
pomaga w porównaniach między gospodarkami poszczególnych krajów
np. gospodarki krajów gdzie poziom cen jest generalnie niższy (mierzone np. za pomocą PNB) przy użyciu parytetu siły nabywczej są oceniane jako większe niż w cenach absolutnych
pomaga ocenić czy waluta danego kraju jest przewartościowana czy niedowartościowana
Efekt Fischera
Efekt Fischera zakłada, że wzrost (spadek) oczekiwanej stopy inflacji krajowej spowoduje proporcjonalny wzrost (spadek) krajowych stóp procentowych
![]()
gdzie :
ih - krajowa stopa procentowa (nominalna)
r - realna stopa procentowa
ph - oczekiwana stopa inflacji w kraju
Przekształcając powyższy wzór otrzymujemy kolejno
![]()
ponieważ przy niewielkiej stopie inflacji i realnej stopie procentowej wyraz ![]()
jest bardzo mały to można go pominąć otrzymując przybliżoną wartość nominalnej krajowej stopy procentowej
![]()
Krajowa stopa procentowa jest więc zależna od realnej stopy procentowej i oczekiwanej stopy inflacji
Analogicznie
Stopa procentowa za granicą jest zależna od realnej stopy procentowej za granica i oczekiwanej stopy inflacji za granicą
![]()
Efekt Fischera c.d.
Aby porównać zależności krajowej i zagranicznej stopy % odejmujemy od równania na krajową stopę procentową równanie na zagraniczną stopę procentową otrzymując
![]()
dzieląc obie strony przez (1+r)
![]()
Wniosek: różnice między stopami procentowymi w kraju i za granicą są proporcjonalne do różnic w stopach inflacji w kraju i za granicą
Wzór na efekt Fischera można przekształcić do postaci
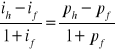
co przy niskiej inflacji i niskich stopach procentowych za granicą można przedstawić jako
![]()
Efekt Fishera sugeruje, że różnice nominalnych stóp procentowych między krajami powinny odzwierciedlać różnice w inflacji powiększone o realną stopę procentową. Jeśli tak się nie dzieje stwarza to okazję do arbitrażu.
Uwaga (!) Założenie, że realna stopa % jest taka sama na całym świecie jest uproszczeniem. W rzeczywistości poszczególne kraje mogą mieć różną realną stopę procentową ze względu na ryzyko polityczne oraz ograniczenia w zakresie przepływów kapitału.
Przykład - przy założeniu braku różnic między realnymi stopami procentowymi
ph = 10% (stopa inflacji np. w Meksyku)
pf = 2% (stopa inflacji za granicą, np. w USA)
r = 2% (realna stopa %, taka sama w kraju i za granicą)
![]()
![]()
![]()
![]()
Wniosek:
Nominalna stopa procentowa w Meksyku powinna być równa nominalne stopie procentowej w USA powiększonej o 8,16%
Wynika to z różnic w oczekiwanych stopach inflacji
Międzynarodowy efekt Fishera
W sposób analogiczny do względnej teorii parytetu siły nabywczej łączy zmiany kursu walutowego ze zmianami stóp procentowych
Jak
zgodnie ze względną teorią parytetu siły nabywczej różnice w stopach inflacji powinny być odzwierciedlane w zmianach kursu walutowego
tak
zgodnie z efektem Fishera różnica między nominalnymi stopami % odzwierciedlane będą w zmianach kursu walutowego
Z prawa jednej ceny wynika, że cena pieniądza na rynkach światowych musi być taka sama, bo w przeciwnym razie będzie miał miejsce arbitraż prowadzący do zrównania tych cen
Jeśli nominalne stopy procentowe, które są ceną pieniądza różnią się daje to podstawy do arbitrażu
Prawo jednej ceny zostanie zachowane jeśli różnica między kursem terminowym a kursem kasowym będzie ekwiwalentna do różnicy między ceną pieniądza
Parytet stóp procentowych wskazuje na związek między różnicami w nominalnych stopach procentowych a różnicą między kursem spot i kursem terminowym
Jeśli znamy roczną stopę procentową to musimy ją sprowadzić do stopy właściwej dla okresu transakcji
Dla potrzeb obliczania kursu terminowego używamy stopy odsetkowej wyrażonej liczbowo a nie procentowo
rynkowych kwotowaniach walut na termin spot (wg stawek kupna/sprzedaży)
rynkowych kwotowaniach depozytów na rynku międzybankowym (wg. stawek przyjęcia i ulokowania depozytu)
ekstrapolowaniu kursu terminowego dla dat łamanych tj. takich dla których na rynku nie wymienia się depozytów
międzybankowe kwotowania terminowe powiększane są o marżę zależną od wielkości transakcji
jeśli stopa procentowa w kraju jest wyższa niż za granicą to cena waluty zagranicznej będzie na termin notowana z premią
premia terminowa waluty zagranicznej oznacza, że waluta zagraniczna będzie kosztować więcej w walucie krajowej
wyższa cena waluty zagranicznej na termin ma skompensować niższe dochody osiągane w tej walucie
jeśli stopa procentowa w kraju jest niższa niż za granicą to cena waluty zagranicznej będzie na termin notowana z dyskontem
dyskonto terminowe waluty zagranicznej oznacza, że waluta zagraniczna będzie kosztować mniej w walucie krajowej
niższa cena waluty zagranicznej na termin ma skompensować wyższe dochody osiągane w tej walucie
rynek walutowy jest efektywny tzn. że wszystkie dostępne publicznie informacje są zawarte w kursie walutowym
inwestorzy nie podejmują ryzyka czyli nie spekulują
wymienili walutę krajowa na walutę zagraniczną po kursie spot s0
zainwestowali otrzymane środki w walucie obcej wg stopy obowiązującej na rynku zagranicznym (1+if) oraz
wymienili kwotę waluty zagranicznej jakiej oczekujemy na koniec tej inwestycji wg kursu terminowego f0 na walutę krajową
pożyczać środki w USA
wymieniać dolary na złotówki po kursie spot
inwestować otrzymane złotówki
wymieniać na termin złotówki wraz z odsetkami na dolary
kapitał zacznie napływać z USA do Polski
wzrośnie popyt na złotówkę na spot a więc nastąpi presja na wzrost kursu kasowego PLN
wzrośnie podaż złotówki na termin a więc nastąpi presja na spadek kursu terminowego PLN
wzrośnie popyt na kredyt w USA a więc nastąpi presja na wzrost stóp procentowych w USA
wzrośnie podaż środków oferowanych na rynku finansowym w Polsce a więc nastąpi presja na spadek stóp procentowych w Polsce
pożyczać środki w Polsce
wymieniać złotówki na dolary po kursie spot
inwestować otrzymane dolary
wymieniać na termin złotówki wraz z odsetkami na dolary (spłacając pożyczkę w dolarach i zatrzymując nadwyżkę, która jest ich zyskiem)
kapitał zacznie napływać z Polski do USA
wzrośnie popyt na dolara na spot a więc nastąpi presja na wzrost kursu kasowego USD
wzrośnie podaż dolara na termin a więc nastąpi presja na spadek kursu terminowego USD
wzrośnie popyt na kredyt w Polsce a więc nastąpi presja na wzrost stóp procentowych w Polsce
wzrośnie podaż środków oferowanych na rynku finansowym w USA a więc nastąpi presja na spadek stóp procentowych w USA
pożyczeniu środków w USA
wymianie środków na PLN
zainwestowanie tych środków w Polsce
wymianie na termin kwoty złotych potrzebnej do spłaty pożyczki dolarowej
zostajemy z zyskiem w złotych (1,08-1,049 = 0,031)
pożyczamy dolary (wg stopy bieżącej 2%),
wymieniamy dolary na euro po kursie spot (po 1,2630),
inwestujemy euro (wg stopy bieżącej 3%)
sprzedajemy euro za dolary na termin (po 1,2658)
Względna teoria parytetu siły nabywczej |
Międzynarodowy efekt Fishera |
po przekształceniu (od obu stron równania odejmujemy 1)
|
po przekształceniu (od obu stron równania odejmujemy 1)
|
Tak więc stopa zmiany kursu walutowego zależy zgodnie
z międzynarodowym efektem Fishera od różnic między krajową i zagraniczną nominalną stopą %
Przykład
ih = 5% (nominalna roczna stopa % w Polsce)
if = 2% (nominalna roczna stopa % w strefie Euro)
s0 = 4,65 (kurs walutowy EUR/PLN)
st = ? (oczekiwany kurs walutowy EUR/PLN za rok)
![]()
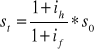
![]()
Wniosek:
Zgodnie z międzynarodowym efektem Fischera oczekiwany kurs EUR/PLN wzrośnie po roku w wyniku różnic stóp procentowych do poziomu 4,7868
Parytet stóp procentowych
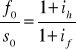
Jeśli nominalna stopa procentowa w kraju jest większa niż stopa procentowa dla inwestycji o takim samym ryzyku za granicą to kurs waluty zagranicznej musi być notowany na termin z premią tzn. musi być wyższy o tyle by zrekompensował niższą stopę procentową.
Jeśli warunek ten nie zostanie zachowany to przy założeniu, że nie ma barier w przepływach kapitałowych dojdzie do arbitrażu.
Parytet stóp procentowych c.d.
Jeśli obowiązuje parytet stóp procentowych to dochód z ekwiwalentnej inwestycji na międzynarodowym rynku pieniężnym będzie taki sam niezależnie od tego w jakim kraju czy w jakiej walucie pieniądz jest inwestowany
Po odjęciu 1 od obu stron otrzymujemy wzór na stopę zmian w kursie terminowym i odpowiednia różnicę w oprocentowaniu
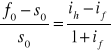
przy niskich stopach procentowych powyższy wzór można uprościć do wersji przybliżonej
![]()
Parytet stóp procentowych obowiązuje pod warunkiem pominięcia kosztów transakcyjnych i braku ograniczeń w przepływach kapitałowych |
Obliczanie kursu terminowego
Ze wzoru na parytet stóp % 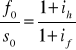
otrzymujemy 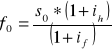
gdzie
f0 - to kurs terminowy waluty zagranicznej
s0 - kurs spot waluty zagranicznej
ih - stopa procentowa w kraju (w okresie transakcji terminowej)
if - stopa procentowa za granicą (w okresie transakcji terminowej)
Forward =
Kurs forward USD/PLN obliczymy z następującego wzoru
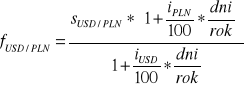
Obliczanie kursu terminowego c.d.
Wzór na kurs terminowy gdy:
walutą zagraniczną jest dolar amerykański
walutą krajową złoty
roczna stopa % w Polsce wynosi 5%
a roczna stopa % w USA wynosi 2%
dla transakcji na 3 miesiące nasze równanie wyglądałoby następująco
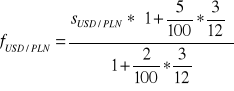
Zasady obliczanie kursów terminowych na rynku międzybankowym
Na tym rynku obliczanie kursów terminowych opiera się na
Zasady obliczania kursów terminowych dla klientów nie-bankowych
Przykład - obliczania kursu terminowego na podstawie parytetu stóp procentowych
s0 - kurs spot USD/PLN = 3,78
f0 - kurs terminowy USD/PLN za 1 rok = ?
ih - roczna stopa % w PLN= 5%
if - roczna stopa % w USD=2%

a więc ![]()
Wniosek:
Kurs terminowy dolara (termin 1-roczny) powinien wynieść 3,8912 aby zachowany został parytet stopy procentowej
s0 - kurs spot USD/PLN = 3,78
f0 - kurs terminowy USD/PLN za 3 miesiące = ?
ih - roczna stopa % w PLN= 5%
if - roczna stopa % w USD=2%
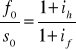
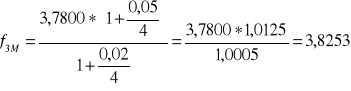
Wniosek:
Kurs terminowy dolara (termin 3-miesięczny) powinien wynieść 3,8253 aby zachowany został parytet stopy procentowej
Premia/dyskonto terminowe
Z parytetu stóp procentowych wynika:
Metoda obliczania wysokości premii/dyskonta
Gdzie:
12 - liczba miesięcy w roku
n- liczba miesięcy na ile zawierana jest transakcje terminowa
powyższy wzór można zapisać też symbolicznie jako
![]()
Przykład obliczania premii/dyskonta terminowego
Dla kursów USD/PLN liczonych dla pełnych miesięcy
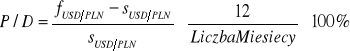
USD/PLN 3,8
USD/PLN(3M) 3,9 (kurs terminowy na 3 miesiące)
Liczba miesięcy 3
![]()
= 0,1053 *100%=10,53%
Kurs dolara na termin jest wyższy niż kurs natychmiastowy
Tzn., że dolar notowany jest w stosunku do złotego z premią, która wynosi w skali roku 10,53%
W notowaniu odwrotnym, gdy PLN jest walutą bazową
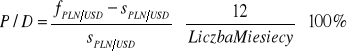
Kurs spot PLN/USD 1/3,8 = 0,2632
Kurs terminowy PLN/USD 1/3,9 = 0,2564
Liczba miesięcy 3
![]()
Złoty notowany jest wobec dolara z dyskontem, które wynosi w skali roku 10,33%
Efekt predykcji kursu kasowego na podstawie kursu terminowego
Zgodnie z tym efektem przewiduje się, że terminowa premia lub dyskonto w kursie terminowym równe jest przewidywanym zmianom w kursie walutowym.
![]()
gdzie:
f0 - kurs terminowy
s0 - kurs bieżący/spot
st - przewidywany kurs spot
Jeśli więc:
f0 - kurs terminowy (3M) USD/PLN = 3,8253
s0 - kurs bieżący/spot USD/PLN = 3,7800
To st = f0 z czego wynika, że
![]()
aprecjacja dolara wyniesie ok. 1,2%
![]()
premia terminowa dolara wyniesie również ok. 1,2%
Efekt ten obowiązuje pod warunkiem, że
Arbitraż stopy procentowej
Polega na wykorzystaniu sytuacji rynkowej kiedy nie jest zachowany parytet stóp procentowych
Równowaga arbitrażowa ma miejsce jeśli
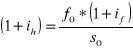
w sytuacji określonej tym równaniem inwestycja w kraju przyniesie przy bieżącym kursie spot, kursie terminowym i stopach procentowych w obu krajach taki sam dochód jak inwestycja za granicą
Porównanie tych dwóch sytuacji polega na stwierdzeniu czy gdybyśmy
to w efekcie uzyskamy taki sam dochód jaki otrzymalibyśmy z inwestycji naszych środków w kraju wg bieżącej stopy % (1+ih)
Arbitraż stopy procentowej c.d.
Jeśli np. porównujemy możliwości inwestowania w Polsce i w USA to
1. w przypadku, gdy bardziej się opłaca inwestować w Polsce otrzymamy następujące nierówności
![]()
lub inaczej ![]()
Z powodu takiej nierówności arbitrażyści zaczną wykorzystywać fakt, że kapitał jest tańszy w USA a droższy w Polsce.
Będą oni :
W efekcie arbitrażu:
Arbitraż stopy procentowej c.d.
2. W przypadku, gdy bardziej się opłaca inwestować w USA otrzymamy następujące nierówności
![]()
lub inaczej
![]()
Z powodu takiej nierówności arbitrażyści zaczną wykorzystywać fakt, że kapitał jest tańszy w Polsce a droższy w USA.
Będą oni :
W efekcie:
Przykład - pokrytego arbitrażu na stopę procentową
f0 - kurs terminowy na 1 rok USD/PLN= 3,8500
s0 - kurs kasowy USD/PLN = 3,78
ih - roczna stopa % w PLN= 8%
if - roczna stopa % w USD=3%
dochód z inwestycji w Polsce
![]()
dochód z inwestycji w USA
![]()
Mamy więc sytuację taką, że
![]()
Wniosek: inwestycja w Polsce daje większy dochód niż w USA
daje to możliwość arbitrażu polegającą na
`Pokryty' arbitraż na stopę procentową polega na wykorzystaniu różnic między stopami bez inwestowania własnych środków
Pokryty arbitraż odsetkowy między USD a EUR
Kurs spot EUR/USD 1,2630
Kurs terminowy EUR/USD 1,2658
Stopa % w EUR 3%
Stopa % w USD 2%
![]()
![]()
Ponieważ zysk z inwestycji może być wyższy w euro a więc:
Kwota inwestycji 100.000 USD
|
Przepływy w USD |
Przepływy w EUR |
Pożyczamy 100.000 USD po 2% |
+100.000 |
|
Wymieniamy na EUR po kursie spot |
-100.000 |
+79.177 |
Inwestujemy w EUR wg stopy 3% na rok Po roku otrzymamy |
|
+2.375 |
Sprzedajemy tę kwotę na termin |
+103.229 |
-81.552 |
Spłata pożyczki w USD wraz z odsetkami |
-102.000 |
|
Zysk arbitrażowy |
1229 |
0 |
Zgodnie z międzynarodowym Efektem Fishera są sobie równe
Zgodnie z zasadą parytetu siły nabywczej są sobie równe
Zgodnie z zasadą parytetu stopy procentowej są sobie równe
Przewidywane zmiany w kursie kasowym
![]()
Względne różnice między kursem kasowym i terminowym
![]()
Względne różnice w stopie oczekiwanej inflacji
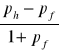
Względne różnice w stopie procentowej
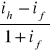
Zgodnie z efektem Fishera są równe
Zgodnie z efektem predykcji są sobie równe
Kurs Terminowy - Kurs Kasowy
Kurs Kasowy
*
12
n
*
100
Premia/dyskonto =
spot*
*
100
rok
dni
stopa % waluty kwotowanej
1+
*
100
rok
dni
stopa % waluty bazowej
1+
Wyszukiwarka
Podobne podstrony:
KompAnSzerCzasW7, Studia - Materiały, Ekonometria
egzam2, Studia - Materiały, Ekonometria
Wykład 5 MINI, studia materiały, EKONOMIA
ek.fin, Studia - Materiały, Ekonometria
core, Studia - Materiały, Ekonometria
Sprawozdanie z Laboratoriów z przedmiotu Ekonometria Fina nsowa 1, Studia - Materiały, Ekonometria
Sprawozdanie z Laboratoriów z przedmiotu Ekonometria Fina nsowa 2, Studia - Materiały, Ekonometria
20080520 Ekonometria szeregow czasowych, Studia - Materiały, Ekonometria
Wykład 5, studia materiały, EKONOMIA
Grupa B, Studia dziennikarstwo i komunikacja społeczna, Ekonomika mediów - pytania i notatki
Biznes plan - praca zaliczeniowa, Studia - materiały, semestr 7, Zarządzanie, Marketing, Ekonomia, F
PESK, studia, studia materiały, Akademia ekonomiczna, Finansowanie projektów ochrony środowiska-Kożu
Ekonomia - definicja i teorie ekonomiczne, Studia - materiały, semestr 7, Zarządzanie, Marketing, Ek
ALIANS na anglika, studia, studia materiały, Akademia ekonomiczna, Finansowanie projektów ochrony śr
Wskaźniki, Studia - materiały, semestr 7, Zarządzanie, Marketing, Ekonomia, Finanse itp
ekonomika wyklady, Transport Polsl Katowice, 6 semestr, Studia 6, Materiały Jacek, Ekonomika transpo
więcej podobnych podstron