dr Anna Barbaszewska-Wiśniowska

RACHUNEK RÓŻNICZKOWY

Zad.1. Korzystając z definicji oblicz pochodną funkcji w podanych punktach

a.

b.

c.

d.

e.
dowolnie ustalone

Zad.2. Korzystając z odpowiednich twierdzeń i wzorów oblicz

a.

b.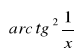

c.
gdzie

d.
gdzie

e.
gdzie

f.

g.
gdzie

Zad.3. Napisz równanie stycznej oraz równanie normalnej do wykresu następującej funkcji

a.
w punkcie

b.
w punkcie

c.
w punkcie

d.
w punkcie

Zad.4. Podaj interpretację geometryczną twierdzenia Rolle'a dla funkcji
na przedziale
i znajdź liczbę
występującą w tezie twierdzenia.

Zad.5. Podaj interpretację geometryczną twierdzenia Lagrange'a dla funkcji
na przedziale
i znajdź punkt, w którym styczna jest równoległa do siecznej przechodzącej przez punkty
.

verte

Zad.6. Sprawdź czy funkcja
spełnia założenia twierdzenia Lagrange'a na przedziale
. Jeżeli tak, to znajdź istniejące
.

Zad.7. Korzystając z wniosku z twierdzenia Lagrange'a wykaż równości

a.

b.

c.

Zad.8. Napisz wzór Taylora z resztą Lagrange'a dla funkcji f we wskazanym punkcie i dla podanego n

a.

b.

c.

Zad.9. Wyprowadź wzory McLaurina z resztą R_n dla funkcji

a.

b.

c.

d.

e.

Zad.10. Wyjaśnij pochodzenie wzorów przybliżonych

a.

b.

Zad.11. Wyznacz przedziały monotoniczności funkcji

a.

b.
s

c.

d.

e.

Zad.12. Wyznacz przedziały wypukłości funkcji (określ charakter wypukłości) oraz znajdź punkty przegięcia

a.
b.
c.

Zad.13. Podaj twierdzenia zwane

a. W.K. istnienia ekstremum funkcji różniczkowalnej

b. I W.W. istnienia ekstremum funkcji różniczkowalnej

c. II W.W. istnienia ekstremum funkcji różniczkowalnej

Zastosuj do znalezienia ekstremów funkcji

d.

e.

Zad.14. Oblicz granice

a.
b.
c.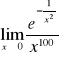
d.

Zad.15. Znajdź asymptoty

a.
b.
c.

---