Metoda Blocha-Schmigalli

Literatura: Martyniak Z. „Metody organizacji i zarządzania”, Wydawnictwo AE Kraków, 1999.

Martyniak Z. „Metody organizowania procesów pracy”, PWE, Warszawa, 1996

Metoda ta polega na rozmieszczaniu obiektów w węzłach siatki trójkątnej i badaniu powiązań między nimi. Pomija się tu rzeczywiste wielkości obiektów zakładając jednakowe odległości (równe przyjętemu modułowi siatki) pomiędzy sąsiadującymi obiektami.

Metoda ta jest uniwersalna, albowiem przy jej zastosowaniu można przeprowadzać optymalizację rozmieszczenia zarówno istniejących jak i projektowanych obiektów. W metodzie zakłada się, że optymalna alokacja obiektów jest wówczas, gdy wartość „Q” funkcji celu wynosi minimum:

gdzie:

Sij -powiązania między obiektem „i” a obiektem „j”,

Lij - odległość (mierzona w przyjętych jednostkach modułowych) między obiektem „i” a obiektem „j”.

Danymi potrzebnymi do rozmieszczenia obiektów jest macierz powiązań pomiędzy obiektami.

Kroki w metodzie Blocha-Schmigalli:

1. Wyznaczenie kolejności lokowania obiektów na siatce.

2. Rozmieszczenie obiektów w węzłach siatki trójkątnej według wcześniej wyznaczonej kolejności.

3. Sporządzenie macierzy odległości i obliczenie wartości funkcji kryterium.

Przykład:

Dana jest macierz powiązań międzyobiektowych:

	1	2	3	4	5	6
1	X
2	200	X
3	100	200	X
4		400	700	X
5		300	200	100	X
6			100	100		X

Etap 1. Wyznaczenie kolejności lokowania obiektów.

W macierzy tej wybieramy parę o największych powiązaniach (element o max S_ij), w przypadku istnienia kilku takich par, parę o największej ilości powiązań z innymi obiektami.

Wypisujemy tę parę pod macierzą i przepisujemy odpowiednie wielkości powiązań.

Następnie dodajemy te wielkości i szukamy maksymalnej sumy, która wskazuje obiekt, który winien być kolejno rozmieszczony jako posiadający największe powiązania z obiektami wytypowanymi do rozmieszczenia.

Kroki ten powtarzamy aż zostaną wytypowane wszystkie obiekty. W przypadku braku jasnego wskazania, do rozmieszczenia wybieramy obiekt o największej liczbie powiązań z największą liczbą obiektów jeszcze nie ustawionych, jeżeli nie ma takiego obiektu to obiekt o największej liczbie powiązań z obiektami już ustawionymi.

	1	2	3	4	5	6
1	X
2	200	X
3	100	200	X
4		400	700	X
5		300	200	100	X
6			100	100		X
3	100	200	-	-	200	100
4	0	400	-	-	100	100
Σ	100	600	-	-	300	200
2	200	-	-	-	300	0
Σ	300	-	-	-	600	200
5	0	-	-	-	-	0
Σ	300	-	-	-	-	200
1	-	-	-	-	-	0
Σ	-	-	-	-	-	200
6	-	-	-	-	-	-

Etap 2. Rozmieszczenie obiektów w węzłach siatki.

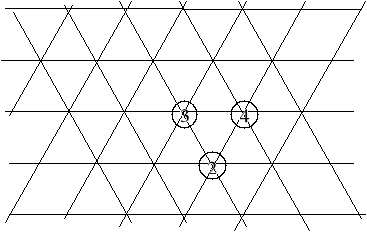
Pierwszą parę umieszczamy obok siebie w centrum siatki.

Kolejny obiekt jeżeli ma powiązania z obydwoma wcześniej ulokowanymi umieszczamy w węźle tworzącym trójkąt wraz z dwoma węzłami już zajętymi. Jeżeli obiekt ma powiązanie tylko z jednym z rozmieszczanych obiektów, umieszczamy go w dowolnym sąsiednim węźle.

Kolejne obiekty umieszcza się w takich miejscach dla których suma powiązań między wszystkimi ustawionymi obiektami jest minimalna. Jeżeli liczba możliwych lokalizacji rozlokowania jakiegoś obiektu jest większa niż jeden, wówczas musimy rozpatrzyć wszystkie możliwe miejsca i spośród nich wybrać to, dla którego wartość powiązań pomiędzy obiektami jest minimalna.

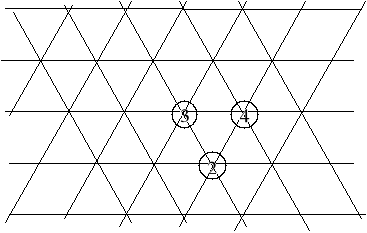
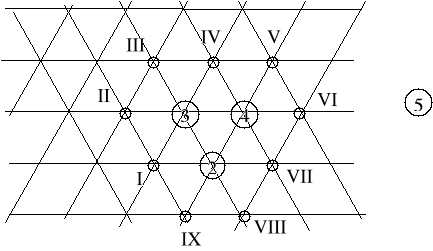
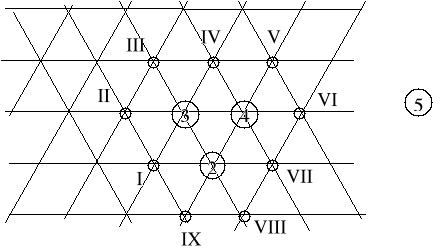
Tabela pomocnicza do ustalania lokalizacji obiektu nr 5.

Powiązane obiekty (wielkości powiązań)	Iloczyny odległości i wielkości powiązań
		I	II	III	IV	V	VI	VII	VIII	IX
5-2 (300)	300	600	600	600	600	600	300	300	300
5-3 (200)	200	200	200	200	400	400	400	400	400
5-4 (100)	200	200	200	100	100	100	100	200	200
SUMA	700	1000	1000	900	1100	1100	800	900	900

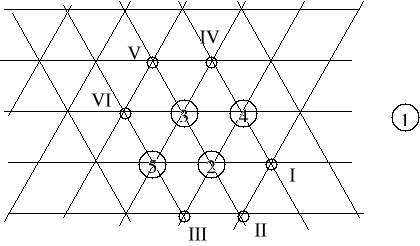
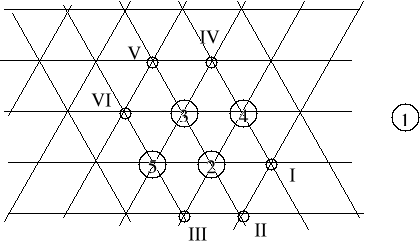
Tabela pomocnicza do ustalania lokalizacji obiektu nr 1.

Powiązane obiekty (wielkości powiązań)	Iloczyny odległości i wielkości powiązań
		I	II	III	IV	V	VI
1-2 (200)	200	200	200	400	400	400
1-3 (100)	200	200	200	100	100	100
SUMA	400	400	400	500	500	500

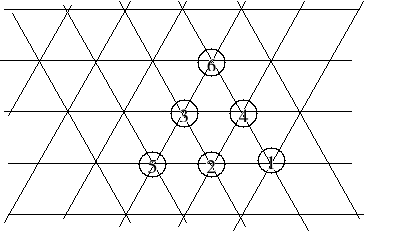
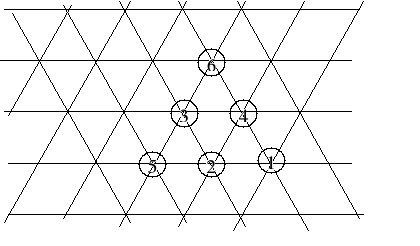
Etap 3. Sporządzenie macierzy odległości i obliczenie wartości funkcji kryterium.

Macierz odległości:

	1	2	3	4	5	6
1	X
2	1	X
3	2	1	X
4	1	1	1	X
5	2	1	1	2	X
6	2	2	1	1	2	X

Wartość funkcji celu:

Q=200*1+100*2+200*1+400*1+700*1+300*1+200*1+
+100*2+100*1+100*1=2600

3

---