[DM 02]

[1/02] Dla każdego z podanych przypadków relacji R ⊆ A² sprawdź czy jest ona:

(i) relacją typu równoważności (jeśli tak to ile wyznacza klas abstrakcji)

(ii) porządkiem częściowym (jeśli tak i jeśli A jest skończone to jaka jest wysokość (A, R)?)

(iii) quasi-porządkiem (jeśli tak i jeśli A jest skończone to jaka jest wysokość (A, R)?)

(iv) porządkiem liniowym

w zbiorze A.

1. A = {1, 2,..., 30}, xRy ⇔ ∀_c∈A[min{x, y} < c ≤ max{x, y} → ∃_d∈A(1 < d < c ∧ d | c)]

2. A = {1,2,..., 1997}, xRy ⇔ x < y - 10

3. A = {1,2,..., 1997}, xRy ⇔ x < y + 10

4. A = {1,2,...,10}², (a, b)R(c, d) ⇔ a | cd ∧ b | cd

5. A = N, xRy ⇔ y = x²

6. A = N, xRy ⇔ x | y ∨ y | x

7. A = N, xRy ⇔ x < y - 1

8. A = N, xRy ⇔ 125 | (x - y)²

9. A jest zbiorem wszystkich funkcji N → R, fRg ⇔ ∀_n∈N(f(n) ≥ g(n))

10. A jest zbiorem wszystkich funkcji N → R, fRg ⇔ ∃_n∈N(f(n) ≥ g(n))

11. A jest zbiorem wszystkich funkcji N → R, fRg ⇔ ∃_n,m∈N(f(n) ≥ g(m))

12. A jest zbiorem wszystkich funkcji N → R, fRg ⇔ ∃_m∈N(∀_n∈N (n ≥ m → f(n) ≥ g(n)))

[2/02] Czy dla każdego skończonego zbioru częściowo uporządkowanego (A, R) istnieje zbiór B ⊆ A² taki, że R ∪ B jest liniowym porządkiem w A?

[3/02] Udowodnij, że jeśli (A, R) oraz (A, S) są zbiorami częściowo uporządkowanymi to (A, R ∩ S) jest także zbiorem częściowo uporządkowanym.

[4/02] Przedstaw diagram Hassego dla zbioru częściowo uporządkowanego (A, R), gdzie R = {(x, y) : x | y}, A = {1, 2,..., 15}. Jak jest wysokość ({1,2,..., 1997}, R)?

[5/02] Czy dla każdego skończonego zbioru częściowo uporządkowanego (A, R) istnieje podział zbioru A na podzbiory P₁, P₂,... takie, że można narysować diagram Hassego tak, aby wszystkie elementy każdego podzbioru P_i znajdowały się na tym samym poziomie i aby co najmniej jeden podzbiór P_i zawierał liczbę elementów równą szerokości (A, R)?

[6/02] Czy dla każdego skończonego zbioru częściowo uporządkowanego (A, R) istnieje podział zbioru A na podzbiory P₁, P₂,... takie, że można narysować diagram Hassego tak, aby wszystkie elementy każdego podzbioru P_i znajdowały się na tym samym poziomie i aby dla dowolnych dwóch elementów x, y ∈ A, takich, że x nakrywa y, zachodziła implikacja x ∈ P_i → y ∈ P_i-1.

[7/02] Podaj przykład zbioru częściowo uporządkowanego, w którym jest nieskończenie długi łańcuch i nieskończenie długi antyłańcuch.

[8/02] Z² (Z - zbiór liczb całkowitych) można interpretować jako nieskończoną szachownicę indeksowaną parami liczb całkowitych. Określamy relację R_F ⊆ Z² × Z² w ten sposób, że (a, b) R_F (c, d) wtwg z pola (a, b) można się dostać na pole (c, d) figurą szachową F w skończonej, dodatniej liczbie ruchów. Udowodnij, że dla każdej figury szachowej F ∈ {wieża, skoczek, goniec, hetman, król} R_F jest relacją typu równoważności. Ile klas abstrakcji w Z² wyznacza każda z 5 relacji R_F ?

[9/02] Rozważamy zbiór A = {2ⁿ : n ∈ N}∪{3} uporządkowany relacją podzielności. Wypisz zbiór elementów minimalnych i maksymalnych w A oraz narysuj diagram Hassego.

[10/02] Niech dany będzie dowolny skończony zbiór częściowo uporządkowany. Udowodnij, że istnienie elementu największego jest równoważne istnieniu dokładnie jednego elementu maksymalnego. Podaj przykład pokazujący, że powyższa równoważność nie musi być spełniona gdy zbiór jest nieskończony.

[11/02] W zbiorze bajtów {0,1}⁸ określono relacje R w ten sposób, że dwa bajty są w relacji, gdy jeden można otrzymać z drugiego przez zamianę dwóch sąsiednich bitów miejscami. Np. 10010001 R 10001001. Czy relacja R jest zwrotna? Czy jest symetryczna? Czy jest przechodnia?

[12/02] Zaznacz w tabeli poniżej, które własności spełniają poszczególne relacje określone w zbiorze liczb naturalnych. Pamiętaj, że 0 ∉ N.

	zwrot­na	syme­tryczna	anty­syme­tryczna	prze­chod­nia	przeciwzwrotna
xRy ⇔ NWD(x, y) > 1
xRy ⇔ NWD(x, y) < 3
xRy ⇔ x + 2y < 2003
xRy ⇔ 5 | (3x + 2y)
xRy ⇔ 5 | (4x + 3y)

[13/02] Na rysunku przedstawiono diagram Hassego relacji porządku częściowego R ⊆ {a, b, c, d, e, f, g, h, j, k, m, n}².

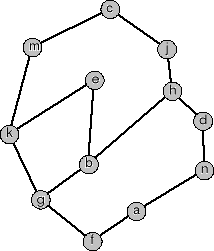
Wyznacz:

1. wszystkie elementy większe od b: _{......................................................................................................}

2. wszystkie elementy mniejsze od b: _{....................................................................................................}

3. wszystkie ograniczenia dolne zbioru {e, j, m}: _{........................................................................}

4. wszystkie ograniczenia górne zbioru {k, b}: _{..............................................................................}

5. kres dolny zbioru {c, e} (jeśli nie istnieje wpisz #):_{..............................................................}

6. kres dolny zbioru {e, h} (jeśli nie istnieje wpisz #):_{.............................................................}

7. wysokość R: _{..........................................................................................................................................................}

8. szerokość R: _{...........................................................................................................................................................}

9. przykład antyłańcucha o liczbie elementów równej szerokości R: _{.........................}

[14/02] Narysuj diagram Hassego dla relacji R ⊆ {x ∈ N : 7 ≤ x ≤ 14} określonej formułą xRy ⇔ x = y ∨ (x < y ∧ ~(3 | xy)). Wyznacz długość najdłuższego łańcucha oraz najliczniejszego antyłańcucha zbioru częściowo uporządkowanego ({x ∈ N : 7 ≤ x ≤ 14}, R).

---