Człon bezinercyjny - człon proporcjonalny, człon wzmacniający; człon dynamiczny podsta­wowy opisywany za pomocą transmitancji ope­ratorowej

G(s) = k

gdzie k — współczynnik wzmocnienia. W cz.b. wielkość wejściowa x(t) jest odtwarzana na wyj­ściu (sygnał y(t)) bez zniekształceń i opóźnień; następuje tylko zmiana amplitudy y (t) = k x(t). Charakterystyka amplitudowo-fazowa cz.b. (rys. a) ma postać punktu o współrzędnych (k, jO).

Przykładem elektrycznego cz.b. jest rezystancyjny dzielnik napięcia (rys. b), gdzie k =R₂/(R₁ + R₂). Przykładem mechanicznego cz.b. jest dźwignia dwuramienna (rys. c). Sygna­łem wejściowym i wyjściowym są tu działające siły x i y, przy czym współczynnik wzmocnie­nia k = l₁/l₂.

Człon całkujący — człon dynamiczny podsta­wowy opisywany transmitancją operatorową

G(s) =k/s

gdzie k — współczynnik wzmocnienia. Odpo­wiedź cz.c. na skok jednostkowy (rys. a) ma postać h(t) = kt.

Charakterystyka amplitudowo-fazowa cz.c. (Rys. b) ma postać

k P(ω) = O oraz Q(ω) =k/ω

Logarytmiczne charakterystyki częstotliwościo­we są pokazane na rys. c, d. Szybkość zmiany sygnału wyjściowego cz.c. jest proporcjonalna do wielkości wejściowej. Przykładem elektrycznego cz.c. jest idealny wzmacniacz operacyjny objęty pojemnościowym sprzężeniem zwrotnym (rys. e). Innym przykładem jest silnik obcowzbudny prądu stałego rozpatrywany pod ką­tem zależności położenia wirnika (y) do napię­cia sterującego (x) przy pominięciu jego elektro­mechanicznej stałej czasowej (rys. f). Przedsta­wiony cz.c. stanowi idealizację członów całku­jących spotykanych w praktyce.

człon inercyjny — człon aperiodyczny (!); człon dynamiczny podstawowy opisywany transmitancją operatorową

; gdzie: k - współczynnik wzmocnienia, T - stała czasowa.

Odpowiedź cz.i. na skok jednostkowy (rys. a) ma postać

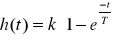
Charakterystykę amplitudowo-fazową tego czło­nu (rys. b) wyraża się zależnością

; oraz

Logarytmiczne charakterystyki częstotliwościo­we pokazane są na rys. c, d. Przykładem elek­trycznego cz.i. jest obwód złożony z rezystancji R i pojemności C (rys. e). Przykładem elektro­mechanicznego cz.i. jest obcowzbudny silnik prądu stałego, sterowany napięciowo (rys. f), rozpatrywany pod kątem zależności prędkości obrotowej (y) od napięcia sterującego (je). W przypadku transmitancji G(s) o postaci

mamy do czynienia z cz.i. niestabilnym. W praktyce przy opisie układów regulacji sto­suje się także cz.i. n-tego rzędu, o transmitancji operatorowej

człon opóźniający — człon dynamiczny podsta­wowy, opisywany transmitancją operatorową

; gdzie: k — współczynnik wzmocnienia, T₀ — czas opóźnienia.

Odpowiedź cz. o. na skok jed­nostkowy (rys. a) ma postać

h(t)=k1(t-T₀);

Charakterystyka amplitudowo-fazowa cz.o. ma postać

P(ω) = k cosωt oraz

Q(ω) = -k sinωt

Jest to okrąg o promieniu równym k i środku w początku układu współrzędnych (rys. b). Logarytmiczne charakterystyki częstotliwościowe są pokazane na rys. c, d. Sygnał wyjściowy cz.o. jest odtworzonym bez zniekształceń sygnałem wejściowym, ale opóźnionym o czas TV Przy­kładami cło. są: linia długa, przenośnik taśmo­wy, rurociąg. Cz.o. jest członem nieminimalnofazowym.

człon oscylacyjny - człon dynamiczny podsta­wowy opisywany transmitancją operatorową w postaci

^; gdzie: k — współczynnik wzmocnienia, ξ- względny współczynnik tłumienia, przy czym O < ξ < l, ω₀ = l/T — pulsacja drgań niewy­muszonych członu. Równanie charakterystycz­ne cz.o. ma dwa pierwiastki zespolone sprzężone
oraz
Przy ξ>= l transmitancja odpowia­da dwom członom inercyjnym połączonym sze­regowo. Odpowiedź na skok jednostkowy cz.o. (rys. a) ma postać

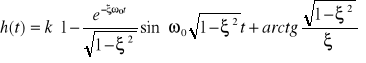
Częstotliwość drgań odpowiedzi skokowej wy­nosi

Charakterystyka amplitudowo-fazowa tego czło­nu (rys. b) wyraża się zależnością

G(jω) = P(ω)+jQ(ω); przy czym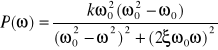
oraz

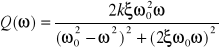
Charakterystyka amplitudowa osiąga swe mak­simum A _m przy częstotliwości rezonansowej

Logarytmiczne charakterystyki częstotliwościo­we Φ(ω) i Lm(ω) są pokazane na rys. c, d. Naj­prostszym przykładem elektrycznego cz.o. jest obwód składający się z indukcyjności L, pojem­ności C i rezystancji R (rys. e). Mechaniczny cz.ο. stanowi układ masy zawieszonej na sprężynie i połączonej z tłumikiem (rys. f). W przypadku transmitancji o postaci
mamy do czynienia z układem niestabilnym.

człon różniczkujący - człon dynamiczny pod­stawowy opisywany transmitancją operatorową

G(s) = ks

gdzie k - współczynnik wzmocnienia. Odpo­wiedź cz.r. ma skok jednostkowy jest impulsem Diraca (rys. a). Charakterystyka amplitudowo-fazowa cz.r. (rys. b) ma postać

P(ω) = 0 Q(ω) = kω

Lm(ω)

Logarytmiczne charakterystyki częstotliwościo­we są przedstawione na rys. c, d. W praktyce nie istnieje możliwość zrealizowania cz.r. o podanej transmitancji operatorowej. Człony rzeczywiste mają na ogół charakter różniczkująco-inercyjny, tj. opisywane są transmitancją

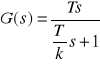
gdzie: T — stała różniczkowania, k — wzmoc­nienie członu dla wielkich częstotliwości (Tω>> 1). Odpowiedzi na skok jednostkowy, charakterystyka-fazowa oraz logarytmiczne charakterystyki częstotliwościowe cz.r. podane są odpowiednio na rysunkach e, f i g. Przykładem rzeczywistego cz.r. jest obwód R, L pokazany na rysunku i.

Uchyb regulacji — s, e; odchylenie regulacji (błąd regulacji (!)); różnica między wartością zadaną Wielkości regulowanej a jej wartością rzeczywistą, czyli e = y₀—y. u.r. jest sumą dwóch składowych, są to: uchyb regulacji przej­ściowy ε_p, istniejący tylko w czasie trwania pro­cesów przejściowych (w stanie nieustalonym) oraz -> uchyb regulacji ustalony ε_u, pozostają­cy również w stanie ustalonym: zatem uchyb re­gulacji zapisujemy w postaci

ε(t) = ε_u(t)+e_p(t)

u.r. jest sygnałem wejściowym regulatora.

uchyb regulacji ustalony - ε_u, ε_s - uchyb ustalony, uchyb statyczny: wartość uchybu regu­lacji w stanie ustalonym, będąca miarą dokład­ności statycznej układu

ε_s = lim ε(t)

Uchyby ustalone oblicza się wykorzystując pojęcie współczynników uchybu. Można wykzać, że dla dostatecznie dużych wartości czasu t przebieg uchybu w układzie regulacji można przedstawić w postaci rozwinięcia w szereg względem pochodnych sygnału wejściowego x(t).

przy czym stałe C_t, zwane współczynnikami uchybu wyrażają się przez pochodne transmitancji uchybowej C_ε(s)

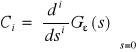
Wartość u.r.u. zależy od transmitancji ukła­du G(s) i postaci sygnału wejściowego

W układzie astatycznym /-tego rzędu C₀ = C₁ = ... = C_1-1 = 0. Różny od zera jest do­piero współczynnik C_t. Układ taki odtwarza bez uchybu ustalonego tylko te pobudzenia, których pochodne począwszy od /-tej są dla dostatecz­nie dużych czasów równe zeru. W układach re­gulacji statycznej wartość uj.u. zależy od współczynnika wzmocnienia k układu otwartego, przy czym zależność ta jest odwrotnie proporcjonal­na. Granicę zmniejszania wartości ε_u, przez po­większenie wzmocnienia układu, wyznacza sta­bilność układu automatycznej regulacji, ściślej - pojawienie się niestabilności.

Linearyzacja równań - sprowadzenie nieliniowego nieliniowego równania różniczkowego do postaci liniowej. Sposób l.r. zależy od rodzaju zjawisk, które dane równanie opisuje, oraz od rodzaju kryterium przybliżenia rozwiązania równania nielinioweg rozwiązaniem odpowiedniego równania liniowego. Najprostszym i najbardziej podstawowym sposobem l.r. jest linearyzacja polegająca na rozwinięciu członów nieliniowych nieliniowych szereg potęgowy i odrzuceniu wyrazów zawierających wyższe potęgi zmiennych przy założeniu, że są one stosunkowo małe. Jeśli np. sygnał wejściowy x związany jest sygnałem wyjściowym y elementu równaniem nieliniowym w postaci F(x,y,y`) = 0, to po rozwinięciu w szereg Taylora wokół punktu równowagi (x°, y°) (stan ustalony, gdzie y° = 0) otrzymamy

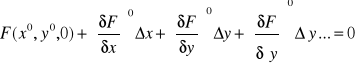
gdzie wskaźnik górny „zero" oznacza wartości pochodnych w punkcie je = x°t y = y° i y = 0. Równanie linearyzowane będzie miało po­stać

Δy+TΔy`=kΔx

Gdzie

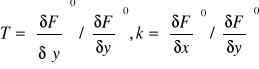
Opisany sposób linearyzacji odgrywa ważną ro­lę przy badaniu stabilności rozwiązań dla ma­łych zmian parametrów wokół punktu równo­wagi (→ Lapunowa metody).

W analizie procesów periodycznych (drgań własnych) \stos. się linearyzację harmoniczną. W analizie procesów losowych stos. się lineary­zację statystyczną.

schemat blokowy -

schemat układu z zazna­czeniem podziału na elementy i bloki funkcjo­nalne z uwzględnieniem ich właściwości dyna­micznych przedstawiający oddziaływania mię­dzy tymi elementami i blokami. Badając dyna­mikę procesów zachodzących w układach auto­matycznego sterowania abstrahuje się od zja­wisk fizycznych stanowiących te procesy, inte­resujące są tylko ich modele matematyczne. S.b. składa się z członów stanowiących model ma­tematyczny pewnych właściwości dynamicz­nych. Dlatego też dany układ automatycznego sterowania może być przedstawiony za pomocą różnych członów, a także jeden człon może od­powiadać procesom o różnym charakterze fi­zycznym. W każdym schemacie blokowym można wyróżnić cztery podstawowe elementy: człony liniowe lub nieliniowe o określonym

kierunku przepływu sygnału; człony porównują­ce (porównawcze) lub człony sumujące, w któ­rych następuje dodawanie lub odejmowanie sy­gnałów; węzły stanowiące punkty, w których następuje rozgałęzienie sygnału; linie skierowa­ne przedstawiające kierunek przepływu sygna­łów. Na rys. przedstawiono typowy schemat blokowy układu z zaznaczeniem tych elementów. S.b. można przekształcić do postaci najbardziej dogodnej z punktu widzenia prowadzonej ana­lizy układu. Zasady przekształcania schematów blokowych noszą nazwę algebry schematów blo­kowych. S.b. spełniają bardzo ważną rolę w ana­lizie układów automatycznego sterowania.

Cykl graniczny — zamknięta trajektoria fazo­wa obejmująca położenie równowagi. Krzywej tego typu odpowiadają ustalone drgania okre­sowe układu

Właściwości cyklu granicznego:

1) cykl jest stabilny, gdy trajektorie fazowe w otoczeniu c.g. zbiegają do niego (rys. a);

2) cykl jest półstabilny, gdy trajektorie fazo­we w otoczeniu c.g. z jednej strony zbiegają do niego a z drugiej zaś rozbiegają (rys. b);

3) cykl jest niestabilny, gdy trajektorie fazo­we w otoczeniu c.g. rozbiegają się od niego (r. c).

Hurwitza kryterium stabilności — kryterium al­gebraiczne oceny stabilności układu polegające na badaniu współczynników równania charak­terystycznego n-tego stopnia układu o postaci

a_nsⁿ+a_n-1s^n-1+…+ a₁s¹+a₀=0

gdzie współczynniki. A_i (i ⁼ 1…n) — są rzeczywiste. K.H. sformułowane jest następująco: warunkiem koniecznym i dostatecznym na to, aby odpo­wiedni stan równowagi układu był stanem sta­bilnym (tzn. aby wszystkie pierwiastki równania charakterystycznego miały ujemne części rzeczy­wiste) jest, aby wyznaczniki złożone ze współczynników. równania charakterystycznego n-tego stopnia aΔ₁, Δ₂, ..., Δ_n były dodatnie oraz współczynniki a₀, a₁,..., a_n były także dodatnie. Jeśli więc wyznacznik

będą tego samego znaku co współcz. a_n to w przypadku gdy współcz. a_n>0, wyznacznik Hurwitza i jego minory główne winny być do­datnie. Zatem z warunków tych wynika waru­nek konieczny stabilności: wszystkie współcz. równania charakterystycznego powinny być do­datnie. Kryterium Hurwitza stos. się zwykle w przypadku równań różniczkowych niższego rzę­du: przy wzroście bowiem stopnia n równania charakterystycznego (np. dla n > 5) obliczanie wyznaczników staje się bardzo złożone i praco­chłonne. Przy uzmiennianiu współcz. równania charakterystycznego a₀,..., a_n układ może osiąg­nąć granice stabilności; wtedy jako pierwszy ze­ruje się wyznacznik Hurwitza stopnia n. Przy dalszej zmianie tych współcz., układ może stać się niestabilny; wtedy liczba zmian znaku w ciągu wyznaczników Hurwitza a_n-1, Δ₂,..,Δ_n jest dokładnie równa liczbie pierwiastków z do­datnią częścią rzeczywistą.

to po rozwinięciu w szereg Taylora wokół punktu równowagi (jc°, y°) (stan ustalony, gdzie j>° = 0) otrzymamy

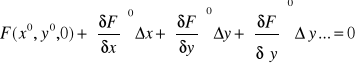
gdzie wskaźnik górny „zero" oznacza wartości pochodnych w punkcie je = x°t y = y° i y = 0. Równanie linearyzowane będzie miało po­stać

Δy+TΔy`=kΔx

Gdzie

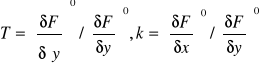
Opisany sposób linearyzacji odgrywa ważną ro­lę przy badaniu stabilności rozwiązań dla ma­łych zmian parametrów wokół punktu równo­wagi (→ Lapunowa metody).

W analizie procesów periodycznych (drgań własnych) \stos. się linearyzację harmoniczną. W analizie procesów losowych stos. się lineary­zację statystyczną.

Nyąuista kryterium — częstotliwościowe kry­terium oceny stabilności zamkniętego układu sterowania na podstawie charakterystyki amplitudowo-fazowej układu otwartego. Sformułowanie tego kryterium jest następujące. Jeżeli układ otwarty jest stabilny, to układ zamknięty jest stabilny wówczas, gdy charakterystyka amplitudowo-fazowa układu otwartego nie obejmuje punktu (-1, j0), przy czym termin „obejmuje" oznacza, że rozpatrujemy wektor, którego początek znajduje się w punkcie (—1, j0), koniec zaś na charakterystyce amplitudowo-fazowej w punkcie odpowiadającym wybranej wartości pulsacji ω (rys. a). Jeżeli cał­kowity kąt obrotu tego wektora przy zmianie wartości co od 0 do +∞ równa się zeru, to roz­patrywana krzywa nie obejmuje punktu (—1, j0). W przypadku gdy układ otwarty jest niestabilny

i m pierwiastków jego równania charaktery­stycznego znajduje się w prawej półpłaszczyźnie zmiennej zespolonej, to układ zamknięty jest stabilny wówczas, gdy charakterystyka amplitu­dowo-fazowa układu otwartego obejmuje -hm/2 razy punkt (—1, jO) przy zmianie wartości o> od O do +00 (znak „plus" dotyczy obrotów w kierunku przeciwnym do ruchu wskazówek zegara).

Zastosowanie sformułowanego wyżej k.N. do układów astatycznych wymaga pewnego uzu­pełnienia. Równanie charakterystyczne takich układów ma pierwiastki równe zeru. Pierwiastki te przenosi się w sposób umowny do lewej półpłaszczyzny zmiennej zespolonej, a przy zmianie pulsacji a> od -~oo do +00 początek układu współrzędnych obchodzi się z prawej strony po półokręgu o nieskończenie małej śred­nicy — jak to pokazano na rys. b. Jeśli trans-mitancja układu otwartego ma postać

gdzie γ stopień astatyzmu układu, to zgodnie z powyższą modyfikacją można przyjąć, że w pobliżu początku układu współrzędnych s =δe^iφ(0<φ<π/2,δ → 0); Mamy więc

gdzie

Dla ω = 0 należy więc uzupełnić charakterystykę amplitudowo-fazową łukiem o nieskończenie dużym promieniu odpowiadającym kątowi γπ/2 liczonym w kierunku ujemnym. Charakterystykę amplitudowo-fazową układu o transmitancji G(s) = l/s(s+a), uzupełnioną zgodnie z powyższymi rozważaniami przedstawiono na rys. c. Ze względu na trudności związane z prawidłową interpretacją tak zdefiniowanego k.N.. stosuje się często inne jego sformułowanie. Jeżeli układ otwarty jest niestabilny, to układ zamknięty będzie stabilny wówczas, gdy różnica pomiędzy liczbą dodatnich i ujemnych przecięć charakterystyki amplitudowo-fazowej układu otwartego rozpatrywanej dla O < ω < ∞ z ujemną osią liczb rzeczywistych na lewo od punktu (—1, j0) równa się m/2, gdzie m jest liczbą pierwiastków równania charakterystycznego układu otwartego leżących w prawej półpłaszczyźnie zmiennej zespolonej. Przy czym przecięcie jest dodatnie jeżeli punkt, w którym charakterystyka amplitudowo-fazową przy wzroście ω przecina oś rzeczywistą z góry na dół, ujemne zaś jeśli przy wzroście co charakterystyka przechodzi od dołu do góry. Na rys. d pokazano charakterystykę amplitudowo-fazową układu niestabilnego (liczba przecięć dodatnich wynosi l, a przecięć ujemnych — 2). K.N. można stosować do układów liniowych o stałych parametrach. Wykorzystywać je można również do analizy układów z opóźnieniem. K.N. umoż­liwia również określenie wpływu parametrów układu na jakość regulacji.

regulator proporcjonalno-całkująco-różniczkujacy — regulator PID; regulator, którego sygnał wyjściowy u(t) jest proporcjonalny do sumy, utworzonej z sygnału uchybu e(t) całki tego sygnału i jego pochodnej. Równanie regulatora PID ma postać

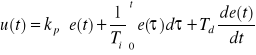
a w formie operatorowej

gdzie: R(s) — transmitancja regulatora, kp = l/x_p — współcz. wzmocnienia proporcjonalnego, x_p — zakres proporcjonalności, T_i — czas zdwojenia, T_d — czas wyprzedzenia. Regulator PID łączy w sobie cechy dodatkowe regulatora PI i regulatora PD, zapewniając: mały uchyb regulacji w zakresie małych częstotliwości i zerowy uchyb w stanie ustalonym, oraz lepszą (w stosunku do regulatora P lub PI) stabilność układu, przy szerszym zakresie cz. skutecznego działania i szybszej reakcji na zakłócenia.

Własności regulatora PID spotyka się najczęściej w regulatorach elektrycznych i pneu­matycznych. Działanie zbliżone do PID mają (dla przebiegów uśrednionych w czasie) niektóre regulatory krokowe.

Regulatory spotykane w praktyce opisuje się równaniem

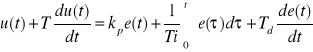
gdzie T — oznacza stałą czasową inercji regu­latora T < Td.

W przypadku T = O uzyskuje się idealny regalator PID, który nie jest możliwy do zrealizawania fizycznie.

regulator proporcjonalno-całkujący — regulator PI; regulator, którego sygnał wyjściowy u(t) jest proporcjonalny do sumy sygnału uchybu e(t) i całki tego sygnału. Równanie regulatora PI ma postać

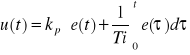
a w formie operatorowej

gdzie: R(s) — transmitancja operatorowa, kp = 1/x_p — współcz. wzmocnienia, xp — zakres proporcjonalności, Ti — czas zdwojenia. Regulatory PI należą do najbardziej rozpowszechnionych, łącząc w sobie zalety regulatora P oraz regulatora I; w zakresie małychcz. i w stanie ustalonym dominuje działanie I, zapewniając małe wartości uchybu i zerową wartość uchybu w stanie ustalonym, w zakresie dużych częstotliwości dominuje działanie P, dzięki czemu regulator nie daje ujemnego przesunięcia fazowego i przez to nie pogarsza stabilności układu. Oprócz licznych regulatorów elektrycznych, pneumatycznych i hydraulicznych, własności zbliżone do PI (dla przebiegów uśrednionych w czasie) mają niektóre regulatory krokowe.

Regulatory spotykane w praktyce opisuje się równaniem

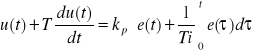
gdzie T oznacza stałą czasową inercji regulatora.

W przypadku, gdy wartość T jest pomijalnie mała i można założyć, że T = 0, uzyskuje się. idealny regulator PI.

regulator proporcjonalno-różniczkujący — regulator PD; regulator, którego sygnał wyjściowy jest proporcjonalny do sumy sygnału uchybu e(t) i pochodnej tego sygnału. Równanie regulatora PD ma postać

a w formie operatorowej

gdzie: R(s) — transmitancja operatorowa, kp = = l/x_p — współcz. wzmocnienia, x_p — zakres proporcjonalności, Td — czas wyprzedzenia.

Działanie regulatora PD w stanie ustalonym i w zakresie małych cz. jest zbliżone do regulatora P, dając m.in. uchyb ustalony regulacji. Zadaniem części różniczkującej (D) jest ułatwienie utrzymania stabilności układu, przez wprowadzenie dodatniego przesunięcia fazowego w zakresie większych częstotliwości. W efekcie otrzymuje się zazwyczaj poszerzenie zakresu cz. skutecznego działania regulatora, czyli przyspieszenie reakcji na zakłócenia. Przy obiektach o stosunkowo dużym opóźnieniu (czas martwy) stosowanie regulatorów PD korzyści nie daje. Własności PD mają niektóre regulatory elektryczne, pneumatyczne i hydrauliczne (rzadziej niż PI). Własności zbliżone do PD mają (dla przebiegów uśrednionych w czasie) niektóre regulatory dwupołożeniowe z korekcją.

Regulatory spotykane w praktyce opisuje się równaniem

gdzie T — oznacza stałą czasową inercji regulatora T < T_d. W przypadku T = 0 uzyskuje się idealny regulator PD, który nie jest możliwy do zrealizowania fizycznie.

regulator proporcjonalny — regulator P; regulator, którego sygnał wyjściowy u(t) jest proporcjonalny do sygnału uchybu e(t). Równanie regulatora P ma postać

u(t)=k_pe(t)

a w formie operatorowej

gdzie: R(s) — transmitancja operatorowa regulatora, k_p = l/x_p — współcz. wzmocnienia pro porcjonalnego, xp — zakres proporcjonalności Cechą charakterystyczną regulatora P jest istnienie uchybu ustalonego regulacji (tzw. statyzm). Własności proporcjonalne ma większość regulatorów bezpośredniego działania, niektóre prostsze regulatory elektryczne, pneumatyczne i hydrauliczne oraz — dla przebiegów uśrednionych w czasie — regulator dwupołożeniowy.

Regulatory spotykane w praktyce opisuje się równaniem.

przy czym T oznacza stałą czasową inercji regulatora. W przypadku gdy wartość T jest pomijalnie mała i przy założeniu, że T = O uzyskuje się idealny regulator P.

sprzężenie zwrotne - wprowadzenie na wejście układu dynamicznego (urządzenia sterują­cego lub obiektu) oprócz innych wielkości wejś­ciowych informacji o jego wielkości wyjściowej, tzn. wprowadzenie sygnału związanego funkcjo­nalnie z przebiegiem wyjściowym tego u-kładu (rys.).

W przypadku, w którym na wejście układu podaje się bezpośrednio jego
sygnał wyjściowy s.z. nazywa się pełnym. Dzię­ki zastos. s.z. zmiany wielkości wyjściowej od­działują w określony sposób na przebieg tejże wielkości wejściowej (-> sprzężenie zwrotne ujemne, —>• sprzężenie zwrotne dodatnie).

Odpowiedni dobór członu s.z. (lub w przy­padku s.z. pełnego dobór urządzenia sterujące­go) pozwala osiągnąć z góry zadane własności dynamiczne i statyczne otrzymanego układu za­mkniętego.

Projektowanie liniowych układów dynamicz­nych ze s.z. mającym pożądane własności pro­wadzi się zwykle metodami: częstotliwościową lub miejsc geometrycznych pierwiastków. Do badania układów z regulatorami przekaźniko­wymi najczęściej stos. się analizę przebiegów czasowych w układzie przy wolnozmiennych sy­gnałach wejściowych.

sprzężenie zwrotne dodatnie - szczególny przy­padek sprzężenia zwrotnego układu regulacji automatycznej doprowadzajmy do powiększe­nia niezgodności między wymaganą wartością wielkości regulowanej (wyjściowej), a jej war­tością rzeczywistą. Z fi­zycznego punktu widze­nia sygnał wejściowy
URA oraz sygnał s.z.d. sumują się. S.z.d. pro­wadzi najczęściej do niestabilności układu.

Formalnie można przyjąć, że ze s.z.d. ma­my do czynienia wtedy, kiedy sygnałowi sprzę­żenia przypisano znak dodatni. Prowadzi to do założenia, że sygnał s.z.d. i sygnał wejścio­wy dodają się. Pojęcie s.z.d. ma charakter umowny i wiąże się z przyjęciem określonej konwekcji strzałkowania sygnałów na schema­cie strukturalnym układu. Transmitancja linio­wego stacjonarnego URA ze s.z.d. ma postać (rys.)

, gdzie G1(s) — transmitancja układu otwarte­go, G2(s) — transmitancja członu sprzężenia zwrotnego.

Sprzężenie zwrotne ujemne - szczególny przy­padek sprzężenia zwrotnego układu automa­tycznej regulacji polegającej na zmniejszaniu niezgodności między wymaganą wartością "wielkości regulowanej (wyjściowej) a jej wartością rzeczywistą. Zasada s.z.u. jest podstawą działania URA, w ten bowiem sposób można przeciwdziałać zakłóceniom powodu­jącym niepożądane zmiany wielkości re­gulowanej.

Formalnie można przyjąć, że ze s.z.u. mamy do czynienia wtedy, kiedy sygnałowi
sprzężenia przypisano znak ujemny, co jest równoważne założeniu podawania na wejście układu otwartego różnicy sygnału wejściowego i sygnału s.z.u.

Transmitancja liniowego URA o stałych współcz. z s.z.u. ma postać (rys.)

gdzie G₁(s) — transmitancja układu otwartego, G₂(s) — transmitancja członu s.z.u. Pojęcie s.z.u. ma charakter umowny, podobnie jak sprzężenie zwrotne dodatnie.

---