Charakterystyka prądowo-napięciowa źródła sem..

Jeżeli prąd pobierany ze źródła sem jest równy zeru, to napięcie na zaciskach tego źródła jest równe sile elektromotorycznej.

Zmiany napięcia na zaciskach źródła: u_E(t)=e(t)-R_W*i_E(t)

Zmiany prądu płynącego przez źródło (w zależności od napięcia na zaciskach): i_E(t)=e(t)/R_W - u_E(t)/R_W = i_ź - G_w*u_E(t) .. i_ź-wydajność prądowa źródła, G_w-przewodność wewnętrzna źródła

Charakterystyka prądowo-napięciowa źródła sem jest opadającą linią prostą, której nachylenie jest proporcjonalne do wartości rezystancji wewnętrznej źródła R_w. W przypadku idealnych źródeł- linia prosta równoległa do jednej z osi. Punkt przecięcia z osią napięcia odpowiada stanowi jałowemu źródła (zaciski źródła są rozwarte, a prąd ma wartość równą zeru)-napięcie jest wtedy równe sile em. Punkt przecięcia z osią prądu odpowiada stanowi zwarcia źródła. Napięcie między zaciskami jest równe zeru, a pobierany ze źródłą prąd Iź jest ograniczony jedynie przez rezystancję wewnętrzną źródła R_w. Prąd jest równy wydajności prądowej źródła I_ź. Wartość napięcia na zaciskach źródła w stanie jałowym oraz wydajność prądowa źródła są podstawowymi parametrami charakteryzującymi źródło sem. Moc zwarciowa (max szybkość pobierania energii ze źródła) jest równa iloczynowi napięcia w stanie jałowym i prądu w stanie zwarcia.

Wartość chwilowa- wartość, jaką sygnał przyjmuje w danej chwili. Oznaczana małą literą x lub x(t)

Wartość skuteczna prądu- wartość prądu stałego, który przepływając przez niezmienną rezystancję R w czasie okresu T, spowoduje wydzielenie na tej rezystancji takiej samej ilości ciepła, co prąd okresowo zmienny w tym samym czasie.

I=pierwiastek z (1/T *caÅ‚ka i²dt) i-wartość chwilowa prÄ…du I-wartość skuteczna

Wartość skuteczna napiÄ™cia- U=pierwiastek z (1/T caÅ‚ka u²dt)

Moc czynna (P)

Jest to wartość Å›rednia mocy chwilowej w okresie T. Moc czynna P=1/T caÅ‚ka pdt… P=1/T caÅ‚ka U*I*cosφ dt=U*I* cosφ ,gdzie: U,I- wartoÅ›ci skuteczne napiÄ™cia i prÄ…du, cosφ- kÄ…t przesuniÄ™cia fazowego miÄ™dzy napiÄ™ciem i prÄ…dem (zwany współczynnikiem mocy).

Moc czynna jest nieujemna. Wartość największą (P=U*I) moc osiąga wtedy, gdy φ=0 (tzn gdy odbiornik jest rezystancyjny, cosφ=1), a wartość najmniejszą (P=0) gdy odbiornik jest cewką idealną lub kondensatorem idealnym, cosφ=0).

Im mniejsze jest przesunięcie fazowe napięcia względem prądu, tym większa jest moc czynna. Odpowiada ona energii jaka wydziela się w jednostce czasu w postaci ciepła w elementach rezystancyjnych.

Moc czynna można wyrazić w trzech równoważnych postaciach: P=U*I*cosφ = R*I² = G*U²

JednostkÄ… mocy czynnej jest wat (1W)

Moc czynna sygnałów sinusoidalnie zmiennych- jest równa iloczynowi wartości skutecznych (połowie iloczynu wartości maksymalnych) tych sygnałów pomnożonemu przez cosinus kąta przesunięcia fazowego między nimi: P=1/2 U_mI_mcosφ

Moc pozorna (S) S=U*I … jest to wielkość charakteryzujÄ…ca urzÄ…dzenia elektryczne, które majÄ… okreÅ›lone znamionowe wartoÅ›ci napiÄ™cia i prÄ…du, wynikajÄ…ce z wytrzymaÅ‚oÅ›ci izolacji i dopuszczalnych wartoÅ›ci prÄ…du ze wzglÄ™du na nagrzewanie lub dziaÅ‚anie siÅ‚. Moc pozorna jest równa najwiÄ™kszej wartoÅ›ci mocy czynnej.JednostkÄ… mocy pozornej jest woltoamper (1V*A). Współczynnik mocy alfa=cosφ to stosunek mocy czynnej do mocy pozornej. Moc pozornÄ… można wyrazić w trzech równoważnych postaciach: S=U*I = Z*I² = Y*U²

Pulsacja (częstość kołowa) - wielkość określająca, jak szybko powtarza się zjawisko okresowe. Pulsacja jest powiązana z częstotliwością (f) i okresem (T) poprzez następującą zależność:

. ω - pulsacja (wyrażana w radianach na sekundę), 2π - kąt pełny (2π radiana = 360 stopni).

Pulsacja jest stosowana najczęściej w technice do określania przebiegów sinusoidalnych.

Twierdzenie Thevenina:

Dowolny aktywny obwód liniowy można od strony wybranych zacisków zastąpić obwodem równoważnym, złożonym z dwóch szeregowo połączonych elementów:- aktywnego, idealnego źródła napięcia o sile elektromotorycznej równej napięciu między wybranymi zaciskami w stanie jałowym,,,,-biernego o impedancji równej impedancji zastępczej rozpatrywanego obwodu widzianej od strony wybranych zacisków, gdy niezależne źródła zasilania są nieaktywne.

Rezystor (R) - element bierny obwodu elektrycznego. Jest elementem liniowym: spadek napięcia jest wprost proporcjonalny do prądu płynącego przez opornik. Przy przepływie prądu zamienia energię elektryczną w ciepło. Występuje na nim spadek napięcia. W obwodzie służy do ograniczenia prądu w nim płynącego.
; gdzie
- rezystywność,
- konduktywność

Cewka (L) - dwójnik pasywny zachowawczy, zdolny do gromadzenia energii w polu magnetycznym, element idealny.
; ØÞ=N·Φ;
;
;

Kondensator (C) - dwójnik pasywny zachowawczy, zdolny do gromadzenia energii w polu elektrycznym, element idealny.
;
;

Rezonans- jest to taki stan pracy obwodu elektrycznego, w którym reaktancja (opór bierny) wypadkowa obwodu lub jego susceptancja(przewodność bierna) wypadkowa jest równa zeru.

Obwodami rezonansowymi są nazywane obwody elektryczne, w którym występuje zjawisko rezonansu.W stanie rezonansu napięcie i prąd na zaciskach rozpatrywanego obwodu są zgodne w fazie, tzn. argument impedancji zespolonej obwodu lub admitancji zespolonej jest równy zeru (ϕ=0).. Obwód będący w stanie rezonansu nie pobiera ze źródła mocy biernej. Moc. Znaki mocy biernej, indukcyjnej i pojemnościowej są przeciwne, dlatego w warunkach rezonansu całkowita moc bierna obwodu też jest równa zeru. . Częstotliwość, przy której reaktancja wypadkowa lub susceptancja wypadkowa obwodu jest równa zeru, jest nazywana częstotliwością rezonansową i oznaczana f_r. Obwód elektryczny osiąga stan rezonansu, jeśli częstotliwość doprowadzonego do obwodu napięcia sinusoidalnego jest równa częstotliwości rezonansowej..W zależności od sposobu połączenia elementów R,L,C, w obwodzie może wystąpić zjawisko rezonansu napięć lub zjawisko rezonansu prądów.

Chwilowe zmiany prądu przez kondensator od napięcia: i(t) = (E/R)*e^-t/τ gdzie stała czasowa obwodu τ równa iloczynowi rezystancji i pojemności występujących w obwodzie:

Ï„ = RC

Narysuj i opisz ch-ke pradowo-napięciową :
Zależność prądu płynącego przez złącze od napięcia polaryzującego

Charakterystyczne zakresy pracy złącza oznaczone są różnymi kolorami:

- czerwony (polaryzacja w kierunku przewodzenia) - U < U_D, złącze praktycznie nie przewodzi, prąd jest bardzo mały; - niebieski (polaryzacja w kierunku przewodzenia) - U > U_D, złącze przewodzi, wraz ze wzrostem napięcia prąd znacząco rośnie; - zielony (polaryzacja w kierunku zaporowym) - płynie niewielki prąd unoszenia; - źółty (polaryzacja w kierunku zaporowym) - przebicie lawinowe lub zenera, prąd gwałtownie rośnie

Jaka powinna byc wartośc impedancji obc. ukl (rys) przy ktorej moc czynna odbiornika bedzie maks. Wyznacz wartośc tej mocy impedancja Z = R + jX ; Zw = Rw + jXw Równanie opisujące moc czynną odbiornika przyjmuje postać: (E -wart. skuteczna źródła napięcia

P = R E2/(R+Rw)2 + (X+Xw)2 Moc jest max. dla X = −Xw
Dopasuj rezystancje obciazenia ukladu ktorego moc czynna bedzie maksymalna W celu wyznaczenia maksimum mocy czynnej odbiornika w zależności od rezystancji obciążenia R zróżniczkować wyrażenie na moc czynną P względem R i przyrównać do zera:

(Rw − R)(Rw + R) = 0

Jeżeli Rw > 0 oraz R > 0, to warunek jest spełniony tylko wtedy,

gdy zachodzi poniższa równość:

R = Rw

Jeżeli mamy prąd o sygnale trójkątnym i chcemy obliczyć jego jego wartość średnią to powinniśmy skorzystać ze wzoru:

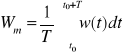
Gdzie: T = okres
w(t) = i(t) = prÄ…d
(całka to pole pod wykresem) -wykorzystamy wzór na pole trójkąta. 1/2*a*h,gdzie
a = T = okres
h = i(max) = prÄ…d max
..mamy:
Wm = 1/T * 1/2 * T * i(max)
Jeżeli jedno z pól jest pod wykresem to ma ono wartość ujemną, czyli musimy je odjąć od reszty np tak było w zadaniu w którym trzeba policzyć wartość średnią prądu na zasilaniu układu. Jeden z trójkątów wypadał pod wykresem. Pola poszczególnych figur sumujemy: prostokąt + trójkąt + trójkąt + (- trójkąt) i mnożymy razy 1/T .

---