Funkcja produkcji dana wzorem ![]()
, gdzie α, β∈(0;1):
Zaliczenie z makroekonomii
Część pierwsza - test wielokrotnego wyboru
Funkcja produkcji dana wzorem ![]()
, gdzie α, β∈(0;1):
charakteryzuje się malejącymi efektami skali przy α+β<1;
charakteryzuje się rosnącymi efektami skali przy α+β>1;
spełnia warunki Inady.
W oryginalnym modelu Solowa:
występują rosnące efekty skali procesu produkcyjnego;
inwestycje determinują inwestycje;
żadna z powyższych.
Jeśli rośnie stopa oszczędności/inwestycji i spada stopa deprecjacji kapitału rzeczowego, to:
spada przyrost kapitału;
rośnie przyrost kapitału;
rośnie stopa wzrostu kapitału.
Techniczne uzbrojenie pracy to:
kapitał ludzki na pracującego;
kapitał ludzki na jednostkę efektywnej pracy;
żadna z powyższych.
Funkcja wydajności pracy opisuje:
relacje pomiędzy K i L a wielkością produkcji;
przyrosty technicznego uzbrojenia pracy;
żadna z powyższych.
Przyrost technicznego uzbrojenia pracy w modelu Solowa zależny jest od:
stopy wzrostu liczby pracujących;
stopy deprecjacji kapitału ludzkiego;
stopy oszczędności/inwestycji.
W modelu MRW:
kapitał ludzki w długookresowej równowadze rośnie szybciej od kapitału rzeczowego;
kapitał rzeczowy w długookresowej równowadze rośnie szybciej od kapitału ludzkiego;
żadna z powyższych.
Równania ruchu modelu MRW opisują:
przyrosty wydajności pracy;
przyrosty produktu na jednostkę efektywnej pracy;
żadna z powyższych.
W stabilnej długookresowej równowadze modelu z endogeniczną akumulacją wiedzy:
produkcja nie ulega zmianie;
produkcja rośnie wolniej od wydajności pracy;
żadna z powyższych.
Złotą reguła akumulacji Phelpsa w modelu Nonnemana-Vanhoudta:
jest stopa inwestycji maksymalizująca stopę deprecjacji kapitału;
jest kombinacja stóp inwestycji wyprowadzająca gospodarkę na najwyżej położoną ścieżkę konsumpcji na jednostkę efektywnej pracy.
jest kombinacja stóp inwestycji wyprowadzająca gospodarkę na najwyżej położoną ścieżkę konsumpcji na pracującego.
W modelu Nonnemana-Vanhoudta:
występuje N zasobów kapitału;
występuje N równań ruchu;
diagram fazowy ma N punktów stacjonarnych.
W modelu typu Solowa z rynkiem pracy:
płace realne równe są krańcowemu produktowi pracy;
krańcowy produkt pracy stanowi stałą część wydajności pracy;
żadna z powyższych.
W długookresowej równowadze modelu typu MRW z rynkiem pracy:
kapitał ludzki rośnie w tym samym tempie, co wydajność pracy;
stopa bezrobocia bezpośrednio oddziałuje na płace realne;
wydajność pracy bezpośrednio oddziałuje na płace realne.
Przy funkcji produkcji danej wzorem ![]()
:
występują stałe efekty skali;
wzrost nakładów K, przy stałych nakładach L, prowadzi do wzrostu krańcowego produktu kapitału.
W modelu MRW spełnione są następujące założenia:
![]()
, gdzie β>0;
![]()
, gdzie L0, n>0;
![]()
, gdzie n>0.
W modelu Nonnemana-Vanhoudta produkt na jednostkę efektywnej pracy spełnia równanie:
![]()
, gdzie α∈(0;1);
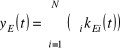
, przy α1, α2, …, αN∈(0;1) i 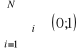
;
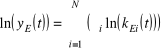
, przy α1, α2, …, αN∈(0;1) i 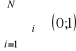
.
W modelu MRW konsumpcję na pracującego opisuje związek:
![]()
;
![]()
;
żadna z powyższych.
W modelu Solowa bez postępu technicznego długookresowa stopa wzrostu produktu równa jest:
g+n;
n;
żadna z powyższych.
Modelem wielokapitałowym jest model:
Solowa;
MRW;
Nonnemana-Vanhoudta.
Złotą regułę akumulacji można wyprowadzić w modelu:
Solowa;
MRW;
Nonnemana-Vanhoudta.
Część druga - zadania (2 do wyboru)
Dane są równania ruchu modelu Nonnemana-Vanhoudta:
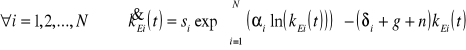
,
gdzie każda ze stóp inwestycji oraz ich suma należą do przedziału (0;1), każda ze stóp deprecjacji i każda z elastyczności należą do tegoż przedziału oraz g, n>0. Podaj interpretację ekonomiczną owych równań (4), wyprowadź kEi (dla i=1,2,…,N) w długookresowej równowadze (3) oraz zbadaj, jak na kEi w długookresowej równowadze wpłynie zmiana δj dla j≠i (3).
Podaj założenia modelu wzrostu Solowa bez postępu technicznego z funkcją produkcji ![]()
wraz z ich interpretacją ekonomiczną (3), wyprowadź równanie przyrostu technicznego uzbrojenia pracy (4) oraz wyznacz techniczne uzbrojenie pracy w długookresowej równowadze (3).
Zdefiniuj pojęcie neoklasycznej funkcji produkcji Y=F(K,L) (3), scharakteryzuj jej właściwości matematyczne (3) i nadaj im interpretację ekonomiczną (4).
Egzamin zerowy z makroekonomii
Część pierwsza - test wielokrotnego wyboru
Jeśli nominalny PKB rośnie o ρ%, zaś ceny o ζ%, gdzie ζ>ρ>0, to:
realny PKB maleje,
w gospodarce występuje inflacja;
żadna powyższych.
Do inwestycji w rachunku PKB nie zalicza się:
wydatków na zakup dóbr pośrednich;
przyrostu zapasów;
żadna z powyższych.
W skład kapitału rzeczowego wchodzi:
wartość wytworzonych dóbr pośrednich;
wartość maszyn, urządzeń itp.;
wartość infrastruktury społeczno-ekonomicznej.
Stopa bezrobocia bezpośrednio zależna jest od:
liczby bezrobotnych;
liczby ludności w wieku produkcyjnym;
liczby aktywnych zawodowo.
Jeśli dodatnia stopa wzrostu realnego PKB jest niższa od stopy wzrostu nominalnego PKB to:
w gospodarce występuje inflacja;
w gospodarce występuje deflacja;
żadna z powyższych.
W modelu mnożnika Keynesa z państwem:
stopa procentowa determinuje inwestycje;
stopa podatkowa determinuje inwestycje;
żadna z powyższych.
W modelu mnożnika Keynesa z państwem:
stopa podatkowa oddziałuje na konsumpcję;
stopa podatkowa oddziałuje na produkcję w równowadze;
LM ma dodatnie nachylenie.
Keynesowski mnożnik w gospodarce bez państwa:
jest wyższy od 1;
jest niższy od krańcowej skłonności do konsumpcji;
jest wyższy niż w gospodarce z państwem.
W modelu IS-LM:
krańcowa skłonność do konsumpcji jest wyższa od 1;
krańcowa skłonność do konsumpcji oddziałuje na nachylenie LM;
żadna z powyższych.
W modelu IS-LM:
wielkość produkcji oddziałuje na popyt spekulacyjny na pieniądz;
inwestycje pośrednio zależne są od stopy podatkowej;
stopa podatkowa nie oddziałuje na wielkość dochodów po opodatkowaniu.
Neoklasyczna funkcja produkcji:
spełnia prawo malejącej użyteczności krańcowej;
spełnia warunki Inady;
jest jednorodna pewnego ujemnego stopnia.
Funkcja produkcji w modelu Solowa:
może być jednorodną stopnia pierwszego funkcją Cobba-Douglasa;
charakteryzuje się malejącymi produkcyjnościami krańcowymi K i L;
żadna z powyższych.
W modelu Solowa:
konsumpcja zależna jest od stopy oszczędności;
oszczędności determinują inwestycje;
produkcja zależna jest od nakładów kapitału ludzkiego.
W modelu MRW:
produkcja niezależna jest od nakładów kapitału rzeczowego;
produkcja zależna jest od nakładów kapitału ludzkiego;
konsumpcja zależna jest od stopy inwestycji w kapitał ludzki.
W modelu Nonnemana-Vanhoudta:
konsumpcja może przewyższyć wielkość produkcji;
produkcja jest wyższa od inwestycji w każdy z zasobów kapitału;
wydajność pracy w długim okresie rośnie szybciej od produkcji.
N>2 równań ruchu jest w modelu:
mnożnika Keynesa;
Solowa;
żadna z powyższych.
Złotą regułę akumulacji Phelpsa wyznacza się w modelu:
IS-LM;
ze sztywną podażą;
żadna z powyższych.
N+1 (N≥2) czynnikowa funkcja produkcji analizowana jest w modelu:
Solowa;
MRW;
Nonnemana-Vanhoudta.
W modelu typu Nonnemana-Vanhoudta z rynkiem pracy:
produkcja rośnie w długim okresie w tym samym tempie, co każdy z zasobów kapitału;
stopa bezrobocia nie oddziałuje na płace;
wydajność pracy oddziałuje na płace.
Modelem równowagi długookresowej jest model:
IS-LM;
Solowa;
MRW.
Część druga - zadania (2 do wyboru)
Podaj założenia modelu IS-LM (4), wyprowadź równanie równowagi rynku produktu (3) oraz podaj jego interpretację ekonomiczną (3).
Dane są równania ruchu modelu MRW:
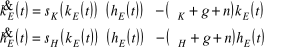
,
gdzie sK, sH, sK+sH, α, β, δK, δH∈(0;1), zaś g, n>0. Podaj interpretację ekonomiczną owych równań (3), skonstruuj diagram fazowy tego modelu (4) oraz pokaż, iż przy kE, hE>0 ma on dokładnie jeden punkt stabilnej równowagi (3).
Podaj założenia modelu typu Nonnemana-Vanhoudta z rynkiem pracy (3) wraz z ich interpretacją ekonomiczną (3) oraz wyznacz długookresową stopę wzrostu produktu (4).
3