Zadania z ekonomii matematycznej

III. FUNKCJA UŻYTECZNOŚCI, JEJ WŁASNOŚCI I CHARAKTERYSTYKI

1. Niech u będzie funkcją użyteczności. Czy funkcja postaci:

a)
,

b)
,

c)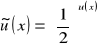
,

d)
,

e)
,

też jest funkcją użyteczności? Odpowiedź uzasadnić.

2. Udowodnij, że wymienione poniżej funkcje użyteczności opisują tę samą relację preferencji:

,
,
,
.

3. Konsument uważa każdy z dwóch towarów za dobro. Towary te można nabyć tylko w jednym z następujących zestawów: A = (1,2), B = (8,4), C = (2,16), D = (4,8). W każdym przypadku dochód konsumenta wynosi 24 zł. Przy cenach
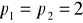
   konsument czasem kupuje zestaw B, czasem zestaw D. Jeżeli ceny wynoszą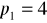
   ,
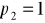
   , to zawsze kupuje zestaw C. Znaleźć funkcję użyteczności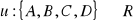
   , która opisuje preferencje konsumenta.

4. Dana jest funkcja użyteczności
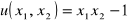
   . Znaleźć krzywą obojętności przechodzącą przez punkt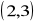
   .

5. Preferencje konsumenta w stosunku do koszyków zawierających nieujemne ilości
   ,
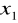
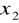
   odzwierciedla funkcja użyteczności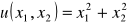
   . Narysować kilka krzywych obojętności. Czy konsument ma wypukłe preferencje?

6. Konsument dwóch dóbr ma funkcję użyteczności daną wzorem
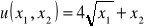
   . Koszyk dóbr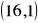
   daje konsumentowi użyteczność 17. Wyznaczyć inne kombinacje dające konsumentowi tę samą użyteczność, jeżeli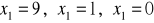
   .

7. Sprawdzić, czy poniższe funkcje użyteczności są rosnące, ciągłe oraz co najmniej dwukrotnie różniczkowalne w
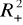
   . Zbadać wypukłość funkcji oraz sprawdzić, czy spełnione jest prawo malejącej krańcowej użyteczności każdego towaru (prawo Gossena).

a)
,

b)
.

8. Konsument spożywając dwa towary A i B kieruje się następującą funkcją użyteczności
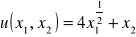
   . Początkowo spożywał 16 jednostek towaru A i 4 jednostki towaru B. Obecnie jego konsumpcja została zredukowana do 4 jednostek towaru A, ale powiększył za to spożycie towaru B w takim stopniu, że nie zmienił poziomu użyteczności. Ile jednostek towaru B spożywa obecnie konsument?

9. Konsument ma funkcję użyteczności daną następującym wzorem

a)
,

b)
,

c)
,

d)
,

e)
.

Wyznaczyć użyteczności krańcowe.

10. Dla funkcji użyteczności podanych w zadaniu 9 obliczyć krańcowe stopy substytucji oraz zinterpretować otrzymane wyniki.

11. Dla funkcji użyteczności podanych w zadaniu 9 a, b, c, obliczyć elastyczności substytucji towaru 1 przez towar 2 dla koszyków x = (1,4) i x' = (5,2). Zinterpretować otrzymane wyniki.

12. Dla funkcji użyteczności podanych w zadaniu 9 d, e, obliczyć elastyczności substytucji towaru 3 przez towar 1 dla koszyków x = (3,1,4) i x' = (10,5,2). Zinterpretować otrzymane wyniki.

13. O ile należy zmniejszyć ilość towaru pierwszego przy zwiększeniu o 6% ilości towaru drugiego, tak aby użyteczność koszyka
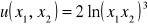
    nie zmieniła się?

14. O ile należy zwiększyć ilość towaru trzeciego przy zmniejszeniu o 3% ilości towaru pierwszego, tak aby użyteczność koszyka
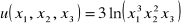
    nie zmieniła się?

6

---