I
1 Zdefiniować i krótko omówić techniczną jakość produktu
Techniczna jakość produktu (wyrobu , usługi) powstaje w dwóch rozłącznych etapach:
podczas projektowania produktu oraz procesu jego realizacji
w procesie produkcji wyrobu lub świadczenia usługi
W związku z powyższym jakość techniczna ma dwie składowe którymi są
jakość typu, jakość projektu
jakość wykonania
Jakość typu - jest relacja między tym zbiorem właściwości użytkowych i technicznych, który został przewidziany w projekcie produktu albo zrealizowany w prototypie a agregatem potrzeb, które produkt ma zaspokajać.
Jakość wykonania - w procesie produkcji wyrobu projekt albo prototyp produktu A jest przekształcany w kolejne jednostki (a) produktu A. Ze względu na to, że żaden proces produkcji lub realizacji usługi nie jest zjawiskiem całkowicie zdeterminowanym przez zadane parametry dlatego zbiory właściwości użytkowych i technicznych kolejnych jednostek produktu A mogą mniej lub bardziej odbiegać od wzorca. Jakość wykonania produktu jest tym wyższa im większa jest zgodność między tymi zbiorami. Jakość wykonania to zatem stopień zgodności wyrobu z wymaganiami projektu. Konieczne jest precyzyjne określenie warunków jakie muszą być spełnione by jednostka produktu mogła zostać uznana za zgodną z projektem lub prototypem. Najczęściej jest to lista dopuszczalnych odstępstw od wzorca. Jakość wykonania odnosi się zarówno do produktu jak i do procesu wytwarzania tego produktu.
Jakość typu i jakość wykonania są kategoriami rozłącznymi. Niedostatki jakości typu tylko w niewielkim stopniu mogą być zrównoważone wysoką jakością wykonania i odwrotnie.
2. Wymienić i krótko omówić podstawowe miary jakości wykonania
Do podstawowych miar jakości wykonania zalicza się wadliwość, poprawność i przeciętną liczbę wad w jednostce produktu. Każda z tych miar może być miarą cząstkową albo agregatową. Z miarą cząstkową mamy do czynienia gdy jakość wykonania oceniana jest ze względu na pojedyncza cechę diagnostyczną (użytkową), jeżeli natomiast pod uwagę brany jest pewien zbiór cech traktowanych łącznie to mamy do czynienia z miarą agregatową.
Wadliwość
Jest podstawową i najczęściej stosowaną miarą poziomu jakości wykonania. Miara ta może być definiowana jako frakcja lub jako prawdopodobieństwo. Wadliwość jako frakcja to frakcja elementów wadliwych czyli nie spełniających wymagań jakościowych w partii albo strumieniu produktu. Wadliwość jako prawdopodobieństwo to prawdopodobieństwo zdarzenia losowego polegającego na tym, że jednostka produktu pobrana ze strumienia lub partii okaże się jednostką wykonaną niepoprawnie, czyli nie spełniającą wymagań jakościowych stawianych danemu produktowi. Wadliwość niezależnie od definicji którą wybierzemy wyraża się liczbą z przedziału [0; 1] lub % z przedziału [0; 100] . Jakość wyrobu jest najwyższa gdy wadliwość=0 a najniższa gdy wadliwość=1. Wadliwość może być miarą poziomu wykonania jedynie wówczas gdy istnieje możliwość i potrzeba dychotomicznej klasyfikacji jednostek produktu z wyróżnieniem jednostek wykonanych poprawnie czyli spełniających stawiane wymagania jakościowe i jednostek , które tych wymagań nie spełniają.
Poprawność
Poprawność jako frakcja jest to frakcja elementów wykonanych poprawnie czyli spełniających wymagania jakościowe w partii albo w strumieniu produktu. Poprawność jako prawdopodobieństwo to prawdopodobieństwo zdarzenia losowego polegającego na tym, że jednostka produktu pobrana z partii lub strumienia okaże się jednostką wykonaną poprawnie czyli spełniającą wymagania stawiane danemu produktowi. Poprawność przyjmuje wartości z przedziału [0; 1] lub [0; 100] jeśli jest wyrażona w %. Jakość wyrobu jest najwyższa gdy poprawność=1 a najniższa gdy poprawność=0.
Przeciętna liczba wad w jednostce produktu
Stosuje się ją gdy nie jest możliwa alternatywna ocena stanu jednostki produktu. Dotyczy to zwykle produktów wytwarzanych w postaci długich odcinków (tkaniny papier przewody energetyczne) lub produktów o bardzo złożonych procesie wytwórczym który nie pozwala na wyprodukowanie produktu całkowicie wolnego od wad.
Norma technologiczna PN ISO 3543-2 dokonała pewnych zmian w zakresie zalecanych miar jakości wykonania. Dokonano bowiem rozróżnienia między wadą a niezgodnością. W miejsce wadliwości zaleca się obecnie stosowanie
frakcji jednostek niezgodnych
procentu jednostek niezgodnych
frakcji jednostek wadliwych
procentu jednostek wadliwych
W miejsce przeciętnej liczby wad w jednostce produktu zaleca się natomiast stosowanie
liczby niezgodności na jednostkę produktu
liczby niezgodności na 100 jednostek produktu
liczby wad na jednostkę produktu
3. Zadanie
p0=10%=0,1
α=0,05 ⇒ Uα dla p=0,95 (1-0,05) wynosi 1,64
ε=0,05 ⇒ Uε dla p=0,95 (1-0,05) wynosi 1,64
n=50
H0: p ≤ p0 H1: p > p0
LC: z0 = n * p0 = 50*0,1=5
GLK: zg = n * p0 + Uα * ![]()
![]()
= 5 + 1,64*![]()
= 5+1,64*![]()
=5+3,48=8,48
DDLK: zdd= n * p0 - Uε * ![]()
![]()
= 5-1,64*![]()
=5-1,64*![]()
=5-3,48=1,52
Dla t=5 występują sygnały o rozregulowaniu procesu, pozostałe punkty świadczą o tym, że proces jest uregulowany. Ponadto dla t=3 , t= 7 i t=8 występują sygnały o korzystnych zmianach w procesie.
4. Zadanie
Kokj |
Kbkj |
Kkkj |
0 |
0 |
0 |
P=20
Cw=15
Cr=5
Cz=4
C(p) =Cdz*p-m(1-p)
0= Cdz*p-m(1-p)
0=Cdz*p-m+m*p
m=Cdz*p+m*p
m=p*(Cdz+m)/:(Cdz+m)
p=![]()
II
1. Zdefiniować i krótko omówić marketingową jakość produktu
Marketingowa jakość produktu jest to relacja między sensorycznym profilem tego produktu a zbiorem potrzeb które ten produkt ma zaspakajać. Operowanie indywidualnymi ocenami jakości możliwe jest tylko w produkcji jednostkowej gdy produkt jest adresowany dla konkretnego odbiorcy mającego swoje wymagania. Profil sensoryczny produktu jest końcowym weryfikatorem jakości produktu. Zadowolenie konsumenta decyduje o poziomie jakości produktu. Podczas zakupu konsument ocenia jakość na podstawie sensorycznego profilu produktu. Profil ten to zespół bodźców zmysłowych odbieranych przez użytkownika przy bezpośrednim kontakcie z produktem, które kształtują obraz produktu w świadomości. Jest to zatem rodzaj informacyjnej otoczki produktu. Do tego profilu produktu nie zalicza się informacji o ułatwieniach kredytowych przy zakupie czy usługach transportowych związanych z dostarczaniem wyrobu nabywcy.
2. Omówić przeciętną liczbę wad w jednostce produktu jako miarę jakości wykonania
Miarę tą stosuje się gdy nie jest możliwa alternatywna ocena stanu jednostki produktu. Dotyczy to zwykle produktów wytwarzanych w postaci długich odcinków (tkaniny papier przewody energetyczne) lub produktów o bardzo złożonych procesie wytwórczym który nie pozwala na wyprodukowanie produktu całkowicie wolnego od wad. Jeśli więc żądamy bardzo długich odcinków musimy pogodzić się z występowaniem wad co jest o tyle łatwiejsze że jeśli wady nie występują zbyt często nie stanowią istotnej przeszkody w użytkowaniu produktu zgodnie z jego przeznaczeniem. Konsekwencja takiego stanowiska jest zaakceptowanie przeciętnej liczby wad w jednostce produktu jako miary wykonania. Pojęcie jednostki (zarówno elementarnej jak i agregatowej) jest niekiedy odnoszone nie tyle do samego produktu co do jego funkcji. Przeciętna liczbę wad można określać ze względu na jedną cechę bądź ze względu na kilka cech traktowanych łącznie.
Norma technologiczna PN ISO 3543-2 proponuje obecnie stosowanie w miejsce tej miary następujących miar:
liczba niezgodności na jednostkę produktu
liczba niezgodności na 100 jednostek produktu
liczba wad na jednostkę produktu
3. Zadanie
p0=10%=0,1
α=0,05 ⇒ Uα dla p=0,95 (1-0,05) wynosi 1,64
ε=0,05 ⇒ Uε dla p=0,95 (1-0,05) wynosi 1,64
n=40
H0: p ≤ p0 H1: p > p0
LC: z0 = n * p0 = 40*0,1=4
GLK: zg = n * p0 + Uα * ![]()
![]()
= 4 + 1,64*![]()
= 4+1,64*![]()
=4+3,12=7,12
DDLK: zdd= n * p0 - Uε * ![]()
![]()
= 4-1,64*![]()
=4-1,64*![]()
=4-3,12=0,88
Dla t=5 występują sygnały o rozregulowaniu procesu, pozostałe punkty świadczą o tym, że proces jest uregulowany. Ponadto dla t=2 , t=3 i t=7 występują sygnały o korzystnych zmianach w procesie.
4. Zadanie
Kokj |
Kbkj |
Kkkj |
0 |
0 |
0 |
P=25
Cw=18
Cr=6
Cz=8
C(p) =Cdz*p-m(1-p)
0= Cdz*p-m(1-p)
0=Cdz*p-m+m*p
m=Cdz*p+m*p
m=p*(Cdz+m)/:(Cdz+m)
p=![]()
V
W jaki sposób rozkład ograniczeń budżetowych konsumentów w danym segmencie wpływa
na politykę jakości firmy oferującej swój produkt na tym rynku
Możliwości zaspokajania potrzeb są korygowane przez ograniczenia budżetowe. Jest to kwota pieniędzy jaką konsument może wydać na zakupy produktów, po zaspokojeniu pilniejszych potrzeb. Ograniczenia budżetowe zależą od dochodów osiąganych przez konsumenta, a także od jego indywidualnej hierarchii potrzeb. Konsumenci reprezentują popytową stronę rynku. Segmentem rynku jest zbiór konsumentów o zróżnicowanych wymaganiach, w odniesieniu do produktów ustalonej klasy. Potrzeby i preferencje są uwarunkowane społecznie, demograficznie i ekonomicznie. Zbadanie preferencji jest podstawą przedsięwzięć marketingowych, zmierzających do określenia optymalnego segmentu rynku dla już istniejących produktów. Z punktu widzenia producenta zarządzanie jakością traktuje się jako segment ogólnego systemu zarządzania firmą. Celem zarządzania jakością jest uzyskanie najwyższej jakości za cenę jaką rynek jest w stanie zaakceptować. Celem jest również osiągnięcie opinii dobrej firmy (marki). Każda klasa produktów ma pewien charakterystyczny dla siebie zbiór cech użytkowych i technicznych. Produkt reprezentuje podażową stronę rynku. Producent może stymulować popyt na oferowany produkt poprzez jakość i żądaną cenę.
Wyjaśnij związek między przeciętną liczba wad jako miarą poziomu jakości wykonania
a parametrem Poissona.
Jakości produktu nie można poprawić przez usunięcie wadliwych jednostek elementarnych. Np. ze wstęgi papieru gazetowego nie można wyciąć jednometrowych wadliwych odcinków ponieważ oznaczałoby to nie poprawę ale drastyczne pogorszenie jakości tego produktu. Ta praktyczna nieusuwalność wadliwych jednostek elementarnych sprawiła, że dla klasy produktów jako miarę jakości zaproponowano przeciętną liczbę wad (niezgodności) w jednostce produktu. Jest to podobnie jak wadliwość miara z inwersją. Tzn. im mniejsza jest przeciętna liczba wad (niezgodności) w jednostce produktu tym wyższa jest jakość wykonania. Miara ta często oznaczana jest symbolem λm w którym m oznacza liczbę jednostek elementarnych wchodzących w skład jednostki użytkowej (agregatowej). Użycie symbolu λm podkreśla związek przeciętnej liczby wad w jednostce produktu z rozkładem Poissona. Przy rozwiązywaniu różnego rodzaju problemów praktycznych λm traktujemy jako parametr tego rozkładu, podobnie jak wadliwość (p) traktowana jest jako parametr rozkładu dwumianowego.
3. Zadanie
λ0=6
α=0,05 ⇒ Uα dla p=0,95 (1-0,05) wynosi 1,64
ε=0,05 ⇒ Uε dla p=0,95 (1-0,05) wynosi 1,64
H0: λ ≤ λ0
H1: λ > λ0
LC: c0= λ0 = 6
GLK: cg = λ0 + Uα * ![]()
= 6+1,64*![]()
=6+1,64*2,45=6+4,02=10,02
DDLK: cdd = λ0 - Uε * ![]()
=6-1,64*![]()
=6-1,64*2,45=6-4,02=1,98
4. Zadanie
Kokj |
Kbkj |
Kkkj |
1 |
0 |
0 |
1 |
0 |
1 |
P=40 m=P-cw=40-30=10
Cw=30 Cdw=cw+cz=30+5=35
Cr=20 Cdz=Cdw+cr=35+20=55
Cokj=1
Ckkj=2
Pokj=0,03
Cz=5
C1(p)=Cokj+Cdzp-m(1-p)
C2(p)=Cokj+Ckkj+Cdwp-m(1-p)
C1(p)=1+55*0,03-10(1-0,03)=1+1,65-9,7= -7,05
C2(p)=1+2+35*0,03-10(1-0,03)=3+1,05-9,7= -5,65
C1(p) < C2(p)
-7,05 -5,65
Wprowadzenie systemu Kkkj jest uzasadnione ekonomicznie
VI
Jakie związki zachodzą pomiędzy jakością produktu a wielkością utargu ze sprzedaży tego
produktu w ustalonym segmencie rynku I ustalonym przedziale czasu
Utarg ze sprzedaży produktu jest iloczynem ceny I ilości sprzedanych jednostek tego produktu. Obecnie potraktujemy go jako funkcje ceny. Można zatem powiedzieć, że:
R(P) = VP
Postać analityczną tego równania można uzyskać mnożąc obydwie strony równania funkcji popytu przez cenę. W przypadku liniowej funkcji popytu otrzymujemy:
R(P) = aP - bP'
Przy ustalonej cenie P' wytwórca produktu o wyższej jakości (A2) uzyskuje nadwyżkę utargu w postaci:
ΔR = P' [V2(P') - V1(P')]
Jeśli natomiast ustalona jest liczba sprzedanych jednostek obu produktów (V') to nadwyżka wynosi:
ΔR = P' [P2(V') - P1(V')]
Również maksymalny utarg R jaki może uzyskać wytwórca produktu o wyższej jakości (A2) jest większy niż maksymalny utarg ze sprzedaży produktu o niższej jakości (A1) . W celu obliczenia maksymalnego utargu należy wyznaczyć pierwszą pochodna funkcji a następnie porównać ją do zera. Otrzymujemy :
P**=a/2b
R*1=a12/4b
R*2=a22/4b
Wynika stąd bezpośrednio, że maksymalny utarg jaki można uzyskać ze sprzedaży produktu o wyższej jakości (R*2) jest większy niż maksymalny utarg ze sprzedaży produktu o niższej jakości (R*1) a różnica między nimi wynosi:
ΔR*=![]()
*(a22 - a12)
Jakie związki zachodzą pomiędzy pojęciem wadliwości produktu lub procesu a parametrem rozkładu prawdopodobieństwa dwuwartościowej zmiennej losowej.
Wadliwość jest jedynym parametrem dwupunktowego rozkładu prawdopodobieństwa zero- jedynkowej zmiennej losowej. W procesie zarządzania i sterowania jakością szczególnie często wykorzystywana jest zmienna losowa postaci:
Zn=![]()
Będąca sumą n-elementowego ciągu zero -jedynkowych zmiennych losowych. Jeśli spełniony jest warunek Ii \ pi = p a więc jeśli prawdopodobieństwo wygenerowania wadliwej jednostki produktu jest jednakowe w kolejnych powtórzeniach procesu to zmienna Zn ma dwumianowy (binomialny) rozkład prawdopodobieństwa o parametrach p i n. Fakt ten zapisać można jako: Zn ∼ B(p, n)
Przy czym B oznacza klasę rozkładów dwumianowych. Zmienna losowa Zn ∼ B(p, n) znajduje bardzo szerokie zastosowanie w statystycznym sterowaniu procesami (SPC) a także w odbiorczych badaniach jakości. Nie wyczerpuje to jednak kręgu zastosowań rozkładu dwumianowego w inżynierii jakości. Znając wadliwość produktu można wykorzystać ten rozkład prawdopodobieństwa do rozwiązywania innych problemów pojawiających się w zarządzaniu jakością.
Zmienną losową Zn o dwumianowym rozkładzie prawdopodobieństwa charakteryzuje się przez :
Zbiór wartości Z0 =(0, 1, 2, ... , n)
Funkcję prawdopodobieństwa P(Zn =z) = (nz) pz (1-p)n-z gdzie z ∈ Z0
Dystrybuantę
Wartość oczekiwaną E(Zn) = np.
Wariancję D2 (zn) = np. (1-p)
3. Zadanie
μ0 = .....
μ = 2,8
σ = 0,6
n = 9
α = 0,05 czyli Uα dla p=0,95 wynosi 1,64
ε = 0,05 czyli Uε dla p=0,95 wynosi 1,64
Trzeba podstawić dane do wzorów dla stymulanty albo destymulanty , narysować wykres i odpowiedzieć na pytanie.
4. Zadanie
Kokj |
Kbkj |
Kkkj |
0 |
0 |
1 |
1 |
0 |
1 |
P=40 m=P-cw=40-30=10
Cw=30 Cdw=cw+cz=30+5=35
Cr=20 Cdz=Cdw+cr=35+20=55
Cz=5
Ckkj=1
Cokj=2
p=0,05
pokj=0,03
C1(p)=kkj+Cdwp-m(1-p)
C2(p)=Cokj+Ckkj+Cdw*pokj-m(1-pokj)
C1(p)=1+35*0,05-10(1-0,05)=1+1,75-9,5= -6,75
C2(p)=2+1+35*0,03-10(1-0,03)=3+1,05-9,7= -5,65
C1(p) < C2(p)
-6,75 -5,65
Wprowadzenie systemu Kokj jest ekonomicznie uzasadnione
VII
1. Wyjaśnić związki między techniczną i marketingową jakością produktu
Jeżeli wszystkie aspekty jakości są na niskim poziomie tzn jest niekorzystna sytuacja techniczna i marketingowa oznacza to że konieczna jest transformacja
Postrzeganie niskiej jakości technicznej jako wysokiej jakości marketingowej - stan taki jest z reguły stanem krótkookresowym wywołanym np. poprzez duże nakłady w sferze promocji i reklamy , który w przypadku braku transformacji jakości technicznej prowadzi najczęściej do stanu w którym wszystkie aspekty jakości są na niskim poziomie.
Niska jakość typu, wysoka jakość wykonania, niska jakość marketingowa - Z taką sytuacją mamy do czynienia gdy zostaje zachwiana równowaga pomiędzy zbiorem właściwości technicznych i użytkowych, który został przewidziany w projekcie produktu albo zrealizowany w prototypie a agregatem potrzeb które projektowany produkt ma zaspokoić.
Wysoka jakość typu przy niskiej jakości wykonania i niskiej jakości marketingowej - Jest to stan świadczący o tym, że koszty poniesione na dobrze wykonany projekt produktu zostały zmarnowane przez niska jakość jego wykonania.
Niska jakość typu, wysoka jakość wykonania i wysoka jakość marketingowa - stan taki może zaistnieć jeśli wytwórcy produktu uda się zrównoważyć niedostatki w jakości typu wysoka jakością wykonania oraz dużymi nakładami na reklamę i promocję. W dłuższym okresie przy braku transformacji jakości typu może dojść do stanu gdzie niska jakość typu pomimo wysokiej jakości wykonania doprowadzi do niskiej jakości marketingowej.
Wysoka jakość typu, niska jakość wykonania, wysoka jakość marketingowa - jest to stan obrazujący sytuację w której pomimo niskiej jakości wykonania producentowi udało się z wykorzystaniem promocji i reklamy przekonać potencjalnego konsumenta że ma do czynienia z wysokim poziomem jakości. Stan taki jest z reguły stanem krótkookresowym i w przypadku braku szybkiej transformacji jakości wykonania może doprowadzić do stanu w którym pomimo wysokiej jakości typu niska będzie jakość wykonania i jakość marketingowa.
Wysoka jakość techniczna, niska jakość marketingowa - z sytuacją taka mamy do czynienia gdy wytwórca produktu nie posiada wystarczających środków finansowych pozwalających wykreować produkt na rynku
Wysoka jakość techniczna, wysoka jakość marketingowa - oznacza korzystną sytuację techniczną i marketingową. Nakłady poniesione na etapie projektowania i wykonania produktu przyniosły zamierzony skutek. Opinia producenta o produkcie pokrywa się z opinią konsumenta.
2.Na czym polega alternatywna ocena właściwości produktu i jak się ja wykorzystuje
w sterowaniu jakością.
Mamy przypadek w którym liczbowym obrazem badanej cechy albo agregatu cech jest zero- jedynkowa zmienna losowa X o realizacjach (x)generowanych według następującej reguły:
x= 0 gdy jednostka produktu spełnia wymagania jakościowe
x= 1 gdy jednostka produktu nie spełnia wymagań jakościowych
Zdefiniowane powyżej zbiory przedstawiają się następująco: X={0; 1} X={0} X={1}. Wynika stąd, że wadliwość jest parametrem rozkładu prawdopodobieństwa obserwowanej zmiennej diagnostycznej X. Im mniejsza jest wartość p(X) tym rzadziej pojawiają się wartości x=1 i tym lepiej świadczy to o wydolności badanego procesu. I odwrotnie im wyższa jest wartość p(X) tym mniejsza jest wydolność procesu , ponieważ oznacza to częstsze pojawianie się jednostek produktu wykazujących brak zgodności z wymaganiami (x=1). Zauważyć należy że wadliwość zależy od tego w jaki sposób zostanie określona reguła według której rozstrzyga się czy badana jednostka produktu spełnia wymagania jakościowe czy też ich nie spełnia. Jeśli reguła ta zostanie określona bardzo liberalnie to nawet bardzo lichy produkt można uznać za dobry. I odwrotnie jeśli reguła ta jest określona bardzo restrykcyjnie to nawet najlepszy produkt może zostać zdyskwalifikowany. Jedyna zatem metoda zapewnienia izomorfizmu między obiektowym systemem relacyjnym a odpowiadającym mu liczbowym systemem relacyjnym jest umowa między dostawcą (producentem) i odbiorcą (konsumentem) . Umowa taka powinna dokładnie precyzować jakie właściwości powinna posiadać poprawnie wykonana jednostka produktu a także jakie odstępstwa są dopuszczalne. Jeśli mamy do czynienia z wielocechowym opisem stanu każdej badanej jednostki produktu to pojawić może się problem dotyczący odpowiedniego zdefiniowania reguły według której dokonywana będzie agregacja ocen cząstkowych.
3. Zadanie
p0=10%=0,1
α=0,05 ⇒ Uα dla p=0,95 (1-0,05) wynosi 1,64
ε=0,05 ⇒ Uε dla p=0,95 (1-0,05) wynosi 1,64
n=45
H0: p ≤ p0 H1: p > p0
LC: z0 = n * p0 = 45*0,1=4,5
GLK: zg = n * p0 + Uα * ![]()
= 4,5 + 1,64*![]()
= 4,5+1,64*2,01=4,5+3,3=7,80
DDLK: zdd= n * p0 - Uε * ![]()
= 4,5-1,64*![]()
=4,5-1,64*2,01=4,5-3,3=1,2
Dla t=5 występują sygnały o rozregulowaniu procesu, pozostałe punkty świadczą o tym, że proces jest uregulowany. Ponadto dla t=2 , t=3 i t=7 występują sygnały o korzystnych zmianach w procesie.
4. Zadanie
Kokj |
Kbkj |
Kkkj |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
P=40 m=P-cw=40-30=10
Cw=30 Cdw=cw+cz=30+5=35
Cr=20 Cdz=Cdw+cr=35+20=55
Cz=5
Cokj=1
Ckkj=2
pokj=0,03
pkkj=0,04
C1(p)=Cokj+Ckkj+Cdw*pokj-m(1-pokj)
C2(p)=Ckkj+Cdw*pkkj-m(1-pkkj)
C3(p)=Cokj+Cdz*pokj-m(1-pokj)
C1(p)=1+2+35*0,03-10(1-0,03)=3+1,05-9,7= -5,65
C2(p)=2+35*0,04-10(1-0,04)=2+1,4-9,6= -6,2
C3(p)=1+55*0,03-10(1-0,03)=1+1,65-9,7= -7,05
C1(p) > C2(p)
C1(p) > C3(p)
III
Omówić strukturę kosztów sterowania jakością i rolę tych kosztów w ogólnej strukturze kosztów jakości
koszty planowania jakości
koszty planowania i projektowania badań rynku w części dotyczącej preferencji konsumenckich
koszty projektowania i realizacji systemów i procedur sterowania jakością
koszty szkolenia pracowników zwłaszcza w zakresie sterowania jakością
koszty odbiorczych badań jakości surowców i materiałów
koszty eksploatacji systemu sterowania jakością w toku produkcji
koszty międzyoperacyjnych i końcowych badań jakości
straty wynikające z niepełnej sprawności diagnostycznej stosowanych procedur pozyskiwania informacji, a także błędów kwalifikacji
straty surowców , materiałów, energii i robocizny zużytej do wytworzenia braków nienaprawialnych
koszty złomowania braków nienaprawialnych
koszty przeróbek i napraw braków naprawialnych
koszty badań i oceny jakości po przeróbkach i naprawach
straty spowodowane utrata nabywców
koszty obsługi strumienia reklamacji jakościowych
odszkodowania za straty poniesione przez konsumentów w związku z użytkowaniem reklamowanego produktu.
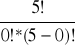
* 1 * (1-p)5 ≤ 0,02(1-p)5 ≤ 0,02 - p ≥ - 1 + 0,996
Ogólny koszt jakości C |
Koszty sterowania Cs |
Koszty prewencji Csr |
|
|
Koszty badań i oceny Csb |
|
Straty na brakach Cd |
Straty na brakach wewnętrznych Cdw |
|
|
Straty na brakach zewnętrznych Cdz |
Koszty prewencji - obejmują wszelkie wydatki w sferze projektowania zaopatrzenia i produkcji, których celem jest zapobieganie stratom na brakach zarówno w sferze produkcji i magazynowania jak i w sferze transportu i handlu. Do grupy tej należą w szczególności
Koszty badań i oceny - obejmują wszelkie wydatki związane z eksploatacją posiadanego systemu sterowania jakością. Należą tu w szczególności:
Straty na brakach wewnętrznych - są to straty generowane przez te wadliwe jednostki produktu które zostały wykryte przez zakładowe służby starowania jakością i które nie przeniknęły do sfery obrotu. Starty obejmują w szczególności:
Starty na brakach zewnętrznych - są to straty generowane przez te wadliwe jednostki produktu które przeniknęły do sfery obrotu. Oprócz wszystkich składników strat na brakach wewnętrznych obejmują one dodatkowo:
Najtrudniejsze do oszacowania i księgowego ujęcia są straty spowodowane utrata nabywców. Poszczególne składniki ogólnego kosztu jakości są wzajemnie powiązane a każdy z nich zależy od istniejących lub przewidywanych uwarunkowań rynkowych. Straty na brakach są pierwotnym źródłem kosztów jakości. Wzrost wydatków jest uzasadniony tylko wówczas gdy służy on ograniczeniu start na brakach, utrzymaniu tych strat na pierwotnym poziomie albo przynajmniej zmniejszeniu tempa ich wzrostu.
2. Zadanie
Producent zamierza sprzedawać swój wyrób w opakowaniach po 5 jednostek . Na jakim poziomie należy utrzymywać produkcyjną wadliwość wyrobu by opakowania zawierające sztuki wadliwe nie pojawiały się częściej niż raz na pięćdziesiąt opakowań. (1 na 50 )
p≤![]()
Pr (Zn > 0 ) ≤ 0,02
Pr ( Zn > 0) = 1 - Pr (Zn = 0)= 1 - (50)*p0 * (1-p)5 - 0 ≤ 0,02
1 - 1 * 1 * (1-p)5 ≤ 0,02 1 - p ≥ ![]()
-(1-p)5 ≤ 0,02 - 1 p ≤ 0,004
(1 - p)5 ≥ 0,98 p ≤ 0,4 %
3. Zadanie
W kolejnych chwilach obserwowano liczbę sztuk wadliwych zt w próbkach o stałej liczebności n=40. Otrzymano następujące wyniki
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
zt |
3 |
0 |
0 |
6 |
3 |
4 |
3 |
3 |
4 |
0 |
0 |
1 |
2 |
0 |
1 |
Skonstruować odpowiednią kartę kontrolną przyjmując prawdopodobieństwo zbędnej regulacji procesu α = 0,05 oraz najwyższą dopuszczalną wadliwość p0 = 0,1. Czy w powyższym ciągu obserwacji występują sygnały o rozregulowaniu procesu albo objawy biernego postępu technologicznego.
n=40 α = 0,05 p0 = 0,1
H0 : p ≤ p0
H1 : p> p0
LC: Zo=np0 =40*0,1= 4
GLK: Zg = np0 + Uα ![]()
= 4+1,645*![]()
=4+1,645 *1,90=7,12
Brak sygnałów o rozregulowaniu procesu , wszystkie punkty świadczą o tym, że proces jest uregulowany. Objawy biernego postępu technicznego występują w pkt 2, 3, 10, 11, 14
qt
t
GLK
DDLK
LC
1,52
5
8,48
qt
t
GLK
DDLK
LC
7,12
4
0,88
LC
DDLK
GLK
t
qt
10,02
6
1,98
qt
t
GLK
DDLK
LC
7,80
4,5
1,20
m=P-cw=20-15=5
Cdz=cw+cz+cr=15+4+5=24
P=![]()
=5:29=0,17 =17%
Największa wadliwość przy której produkcja nie przynosi strat wynosi 17%
m=P-cw=25-18=7
Cdz=cw+cz+cr=18+8+6=32
P=![]()
=7:39=0,179 =17,9%
Największa wadliwość przy której produkcja nie przynosi strat wynosi 17,9%
LC
GLK
t
qt
7,12
4
Wyszukiwarka
Podobne podstrony:
test zarządzanie jakością 21.02, Studia Licencjackie, semestr V, Zarządzanie jakością, dodatek
zarządzanie jakością test 09
4 zarzadzanie jakoscia test 2009 2010 318
zarządzanie jakością test, Pielęgniarstwo- magisterka cm umk, I rok, Zarządzanie w pielęgniarstwie,
test-jako, PWR MBM, Zarządzanie jakością
test market dzienne 2 z odp, STUDIA, WZR I st 2008-2011 zarządzanie jakością, badania marketingowe
jakość TEST, Zarządzanie UE Katowice - licencjat - materiały, zarządzanie UE Katowice - 2 rok - mate
test 1 market, STUDIA, WZR I st 2008-2011 zarządzanie jakością, badania marketingowe
test ANALIZA, STUDIA, WZR I st 2008-2011 zarządzanie jakością, Analiza Finansowa
test market dzienne 1 z odp, STUDIA, WZR I st 2008-2011 zarządzanie jakością, badania marketingowe
Test z systemów zarzadzania jakośćią w elektroradiologii
4 zarzadzanie jakoscia test 2009 2010 318
Zarządzanie Jakością wykład 1
Zarządzanie Jakością Wykład 4
więcej podobnych podstron