Temat 4:

TECHNIKI ANALIZY SYGNAŁU MOWY

Bank filtrów I (historycznie)

• przed opracowaniem FFT widmo mocy, ze względu na zbyt dużą liczbę operacji dla DFT, było estymowane za pomocą banku filtrów - analizowany sygnał był podawany na wejścia zbioru równoległych filtrów pasmowych, na wyjściu których mierzona była energia w każdym analizowanym paśmie. Przebieg reprezentujący energię w każdym paśmie w funkcji czasu był dygitalizowany i zapamiętywany w komputerze;

• metoda analizy za pomocą banku filtrów została pierwotnie opracowana dla potrzeb transmisji mowy w urządzeniu zwanym wokoderem kanałowym (Dudlmy, 1939). Wokoder składa się z dwóch części: analizatora i syntezatora. Analizator składa się z nakładających się filtrów pasmowych, przez które przepuszczany jest sygnał - w każdym kanale dokonuje się pomiaru energii. Dodatkowo mierzy się również częstotliwość podstawową oraz wskaźnik dźwięczności sygnału wejściowego. Syntezator składa się z identycznego banku filtrów, który pobudzany jest przez:

• dla segmentów dźwięcznych: okresowy impuls o częstotliwości podstawowej uzyskanej z analizatora,

• dla segmentów bezdźwięcznych: sygnał szumu losowego.

• zbiór modulatorów amplitudy sterowanych za pomocą sygnałów otrzymanych z analizatora kształtują widmo sygnału wyjściowego syntezatora

• praktycznie ustalono, że potrzeba 10-20 filtrów pasmowych, aby reprodukowana mowa była zrozumiała. W tablicy 1 pokazano parametry banku filtrów wokodera opisanego przez Holmesa (1980), który umożliwił przesłanie mowy strumieniem o objętości 2,4 kbitów/s.

• Analizator wokodera często jest wykorzystywany jako szybka i wygodna metoda otrzymywania widma mocy sygnałów mowy wykorzystywanego następnie w urządzeniach rozpoznawania mowy.

Bank filtrów dla 19-kanałowego wokodera

Nr kanału	Częstotliwość środkowa [Hz]	Szerokość pasma [Hz]
1	240	120
2	360	120
3	480	120
4	600	120
5	720	120
6	840	120
7	1000	150
8	1150	150
9	1300	150
10	1450	150
11	1600	150
12	1800	200
13	2000	200
14	2200	200
15	2400	200
16	2700	200
17	3000	300
18	3300	300
19	3700	500

Bank filtrów II

Ucho ludzkie - nieliniowa analiza widma sygnału mowy.

Zastosowanie nieliniowego przetwarzania częstotliwości zwiększa skuteczność systemów rozpoznawania mowy.

Alternatywa predykcji liniowej - analiza nieliniowa - prosta do wykonania w dziedzinie częstotliwości.

Banku filtrów - bazuje na przekształceniu FFT - bank filtrów liniowych w dziedzinie częstotliwości, o liczbie kanałów równej liczbie próbek analizowanego sygnału.

Idea: prążki widma FFT łączy się w mniejszą liczbę przedziałów częstotliwości (kanałów)

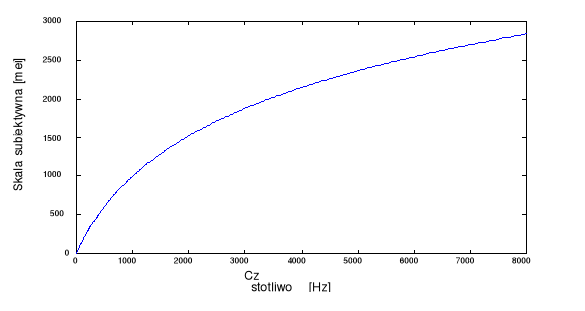
Popularna metoda: skala mel (ang. mel-scale) - bazuje na doświadczalnym związku między częstotliwością czystego tonu harmonicznego i częstotliwością postrzeganą przez człowieka.

Jednostka częstotliwości postrzeganej: mel (Moore, 1989).

Zależność między mel i Hz:

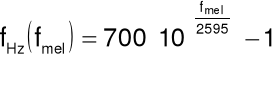
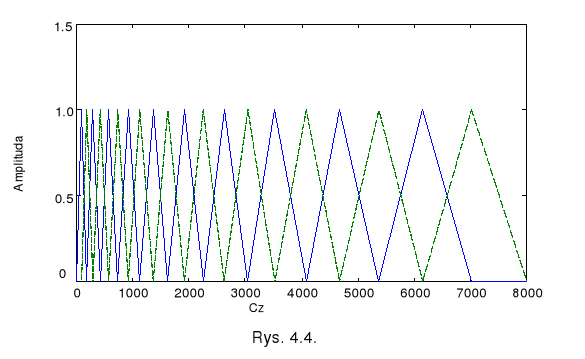
Filtry są równomiernie rozłożone w częstotliwościowej skali mel.

W kanałach filtry mają trójkątne charakterystyki amplitudowe

Przykład

Bank 20 filtrów

każdy o szerokości pasma 300 mel

przesuniętych względem siebie o 150 mel.

Zastosowanie banku filtrów polega na wyznaczeniu:

• widma amplitudowego za pomocą FFT,

• oddzielnie dla każdego kanału w banku: sumy współczynników widma amplitudowego ważonych odpowiadającym im wartościami charakterystyk amplitudowych filtru trójkątnego.

Można zastąpić widmo amplitudowe widmem mocy.

Sumy ważone to parametry banku filtrów.

Najczęściej liczba kanałów z przedziału [12, 20].

Parametry banku filtrów są wysoce skorelowane:

konieczność stosowania pełnej macierzy kowariancji

Transformacja cepstralna parametrów banku filtrów

Współczynniki cepstralne w skali mel

(ang. Mel-Frequency Cepstral Coefficients, MFCC)

Dyskretne przekształcenie kosinusowe logarytmów parametrów banku filtrów:

dla

• 
  - logarytmy parametrów banku filtrów,

• 
  - liczba kanałów (filtrów) w banku filtrów,

• 
  - liczba wymaganych współczynników cepstrum.

Zaleta współczynników MFCC:

uniezależnienie sygnału mowy od wpływu kanału transmisji.

Wydzielanie segmentu za pomocą ramki

Przekształcenie Fouriera do sekwencji ramek:

krótkookresowe przekształceni Fouriera

(ang. Short-Time Fourier Transform, STFT)

Ramka - jeden okres sygnału okresowego

Zastosowanie ramki (okna prostokątnego) - nieciągłości przetwarzanego sygnału - fałszywe wysokie częstotliwości w widmie.

Wygładzenie nieciągłości i usunięcie z widma fałszywych prążków - okna zwężające (tłumiące skrajne próbki).

Okno Hamminga:

dla
.

Wygładzanie to straty w rozdzielczości widma - kolejny argument za nakładaniem ramek.

Analiza czasowo-częstotliwościowa

Sygnał mowy jest sygnałem niestacjonarnym, jego widmo zmienia się w czasie. Oznacza to, że widmo wyznaczone dla wydzielonych z pierwotnego sygnału segmentów będzie różniło się. Zwykle wyniki analizy widmowej dla kolejnych segmentów przedstawia się w postaci spektrogramu, który jest obrazem zmian gęstości widmowej mocy sygnału w funkcji czasu.

Do jednoczesnej analizy sygnału w dziedzinie czasu i częstotliwości wykorzystamy krótkookresową dyskretną transformatę Fouriera (short-term discrete Fourier Transform, STDFT).

Jest to transformata DFT sygnału będącego okresowym przedłużeniem segmentu o postaci
, wydzielonego z sygnału
za pomocą przesuwanego okna
(
). Okno
ma długości
, a o miejscu jego położenia decyduje wartość zmiennej
.

Inaczej mówiąc: segment jest sygnałem
zważonym funkcją okna
, który rozpoczyna się w chwili
, a kończy w chwili
.

Transformata STDFT ma postać:

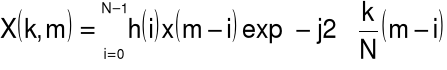
gdzie:

• 
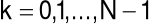
  - numer składowej harmonicznej,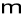

• 
  - miejsce położenia na osi czasu ostatniej próbki wydzielonego segmentu,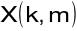

• 
  - wartość składowej harmonicznej o częstotliwości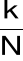
  Hz w widmie sygnału, którego segment kończy się w chwili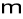
  

• 
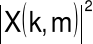
  jest mocą dla częstotliwości k/N Hz i okna o środku w m-(N-1)/2

• czynnik
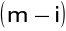
  w wykładniku oznacza, że faza sygnału pozostaje spójna przez zniesienie liniowego przesunięcia fazy wprowadzonego przez opóźnienie o m próbek

• próbki okna są numerowane wstecz w czasie (dla późniejszej wygody) stąd sumowanie jest wykonane do tyłu w czasie

• rozdzielczość częstotliwościowa widma jest 1/N Hz (w jednostkach znormalizowanych)

• widmo jest okresowe i (ponieważ w i x są rzeczywiste) sprzężenie symetryczne

• jest tylko 1/2N +1 niezależnych wartości częstotliwości

Spektrogram

Najczęściej sygnał mowy przedstawia się w postaci tzw. spektrogramu lub śladu głosowego.

Spektrogram jest wyznaczany za pomocą krótkookresowej dyskretnej transformaty Fouriera (short-term discrete Fourier Transform, STDFT). Pokazuje energię w sygnale dla każdej częstotliwości i dla każdej chwili czasu, czyli wyznacza widmo sygnału niestacjonarnego w określonej chwili czasu.

Sygnał jest dzielony na krótkie segmenty (2-40 ms) za pomocą okna, a następnie dla każdego segmentu wyznaczany jest widmo częstotliwościowe za pomocą FFT.

Te spektra są umieszczone jeden obok drugiego, a amplitudy poszczególnych składowych zamieniane na obraz (szary lub kolorowy). Zapewnia to graficzny sposób obserwacji zmian zawartości częstotliwościowej sygnału w czasie.

Długość segmentu jest wybrana jako kompromis między rozdzielczością częstotliwościową (dłuższe segmenty dają lepszą rozdzielczość częstotliwościową) a rozdzielczością czasową (krótsze segmenty dają lepszą rozdzielczość czasową).

W matlabie spektrogram wyznacza się za pomocą funkcji specgram, której opis zastosowania przedstawiono poniżej.

function [yo,fo,to] = specgram(varargin)

%SPECGRAM Calculate spectrogram from signal.

B=SPECGRAM(A,NFFT,Fs,WINDOW,NOVERLAP)

wyznacza spektrogram dla sygnału zapisanego w postaci wektora A. Sygnał jest dzielony na nakładające się segmenty, z których każdy po wymnożeniu przez funkcję okna WINDOW, uzupełnieniu zerami do długości NFFT i poddaniu przekształceniu FFT tworzy kolumnę tablicy B.

Fs jest częstotliwością próbkowania, która nie wpływa na spektrogram, lecz wykorzystywana jest przy skalowaniu wykresów.

Każda kolumna B jest estymatą częstotliwościowej krótkookresowej czasowo zlokalizowanej reprezentacji sygnału A. W tablicy B czas wzrasta liniowo dla kolumn od lewej do prawej strony, a częstotliwość wzrasta liniowo dla wierszy od góry do dołu (początek dla 0).

Dla sygnału A rzeczywistego:

• liczba kolumn B jest k = fix((NX-NOVERLAP)/(length(WINDOW)-NOVERLAP));

• liczba wierszy jest NFFT/2+1 dla NFFT parzystego i (NFFT+1)/2 dla nieparzystego.

NOVERLAP jest liczbą próbek w części segmentów nakładających się.

Gdy WINDOW zostanie zadany jako skalar, wówczas jako okno zastosowane zostanie okno Hanninga o tej długości. Okno musi mieć długość mniejszą lub równą NFTT i większą niż NOVERLAP.

[B,F,T] = SPECGRAM(A,NFFT,Fs,WINDOW,NOVERLAP) zwróci kolumnę częstotliwości F (o długości równej liczbie wierszy tablicy B) i kolumnę momentów czasu T (o długości k), w których spektrogram został wyznaczony.

B = SPECGRAM(A) wyznacza spektrogram sygnału A stosując domyślne wartości parametrów:

• NFFT = minimum(256, długość A),

• Fs=2 Hz

• okno Hanninga o długości NFFT,

• NOVERLAP = length(WINDOW)/2.

Można zastosować wartość domyślną dla dowolnego parametru, zadając go jako [].

SPECGRAM bez argumentów wyjściowych rysuje bezwzględną wartość spektrogramu w aktualnym rysunku, stosując następujące parametry obrazu:

IMAGESC(T,F,20*log10(ABS(B))),

AXIS XY,

COLORMAP(JET).

Czyli składowe o niskiej częstotliwości pierwszej porcji sygnału znajdują się dolnym lewym rogu osi współrzędnych.

SPECGRAM(A,F,Fs,WINDOW), gdzie F jest wektorem częstotliwości w Hz (z przynajmniej dwoma elementami) wyznacza spektrogram dla tych częstotliwości (wykorzystując albo przekształcenia z-chirp dla więcej niż 20 równo rozłożonych częstotliwości lub wielofazowego dziesiętnego banku filtrów).

Przykład

Spektrogramy dwóch wypowiedzi wyrazu „mama”.

Liniowa analiza predykcyjna

Założenie:
-ta próbka sygnału może być prognozowana za pomocą liniowej kombinacji
poprzednich próbek:

.

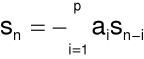
Jest to równoważne założeniu, że trakt głosowy modelowany jest za pomocą filtru rekursywnego o transmitancji:

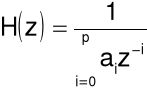
gdzie
jest liczbą biegunów transmitancji oraz
.

Dobór współczynników filtru
:

Minimalizują błąd średniokwadratowy predykcji filtru dla analizowanej ramki.

Agorytm Levinsona-Durbina (matlab)

Metoda autokorelacyjna (biuletyn nr 12)

Wszystkie dotychczas omawiane techniki analizy sygnału mowy nie przyjmowały żadnych założeń na sposób wytwarzania mowy. LPA zakłada, że analizowany sygnał został wytworzony przez przejście sygnału pobudzenia przez odpowiedni filtr. Ponieważ jest to dobry model wytwarzania dla wielu dźwięków, LPA jest szczególnie odpowiednią techniką analizy sygnału mowy.

Jeżeli sygnał
był ciągły, to po jego digitalizacji bieżąca próbka
może być przewidywana (predykowana) z poprzedniej próbki:

,

gdzie współczynnik
jest wybierany tak aby sygnał błędu był mały; np. jeśli sygnał zmienia się liniowo to
będzie stałe.

Ideę przewidywania rozciągniemy na
ostatnich próbek:

lub

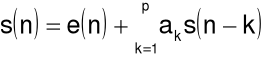
czyli przebieg może być przewidywany na podstawie współczynników
i sygnału
.

Zastosowanie przekształcenia Z do tej równości pozwoli na wyznaczenie transmitancji filtru modelującego trakt głosowy:

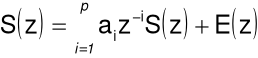
a następnie:

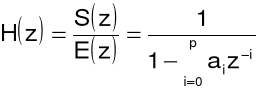
czyli jest to filtr rekursywny (o nieskończonej odpowiedzi impulsowej), a jego schemat strukturalny przedstawia poniższy rysunek.

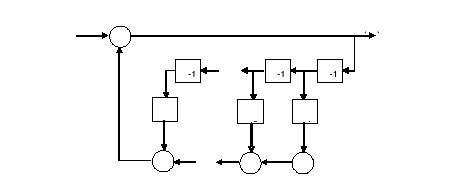
Trakt głosowy jest modelowany za pomocą szeregowego połączenia
odcinków prostej bezstratnej rury, której transmitancja posiada wyłącznie bieguny (ang. all pole model). Zmianie kształtu traktu głosowego przy wymawianiu kolejnych głosek odpowiada zmiana wartości współczynników LPC.

Mimo, że żadne z następujących założeń nie jest ściśle spełnione: trakt wokalny nie jest bezstratny, nie jest utworzony z odcinków rur, posiada odgałęzienia w postaci jamy nosowej, przy generowaniu niektórych głosek, np. trących, jego rola jest znikoma, dla odpowiedniej liczby parametrów LPC można otrzymać rozsądną aproksymację transmitancji traktu głosowego dla wszystkich głosek.

Wyznaczona w ten sposób transmitancja traktu dla poszczególnych głosek może być podstawą do wyznaczenia formantów, będących lokalnymi maksimami ich charakterystyk amplitudowych (odpowiadają za nie bieguny transmitancji). Również formanty są wykorzystywane do identyfikacji głosek, w szczególności dźwięcznych.

Często wykorzystywanym i dlatego interesującym sygnałem jest pobudzenie.

W zadaniu transmisji nazywane bywa sygnałem szczątkowym i charakteryzuje się znacznie mniejszą dynamiką zmian w porównaniu z sygnałem mowy.

Umożliwia także wyznaczenie tzw. częstotliwości podstawowej (tonu krtaniowego), będącej kolejną charakterystyką traktu głosowego.

Można zapisać:

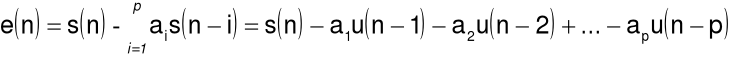
a po zastosowaniu przekształcenia Z:

Transmitancja filtru generującego sygnał błędu predykcji jest następująca:

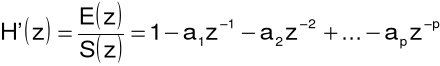
czyli jest to filtr nierekursywny (o skończonej odpowiedzi impulsowej), a jego schemat strukturalny przedstawia poniższy rysunek.

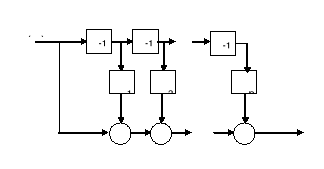
W zadaniach transmisji sygnału mowy dla celów jego kodowania filtr o transmitancji
jest filtrem analizującym (wykorzystywanym w nadajniku), a filtr o transmitancji
jest filtrem syntezującym (wykorzystywanym w odbiorniku). Przy tym są to filtry odwrotne w stosunku do siebie:

.

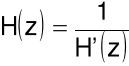
Zwykle do syntezy wystarcza 10 współczynników (wówczas mowa ma akceptowalną jakość).

Problem: jak estymować wartości współczynników.

Współczynniki LPC
dobiera się tak, aby zapewnić minimalizację błędu średniokwadratowego predykcji filtru:

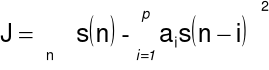
Istnieją różne metody wyznaczania wartości współczynników: różnie można definiować zakres sumowania (zmian
).

Metoda autokorelacyjna: zakres nieskończony. Oczywiście w związku z tym, że sygnał nie może być znany w nieskończonym zakresie, jest on oknowany (tak jest w Matlabie).

Metoda kowariancyjna: zakres sumowania skończony (od
do
).

Cepstrum predykcji liniowej

Transformata Fouriera logarytmu widma tego sygnału

Współczynniki cepstrum:

.

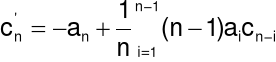
Liczby współczynników cepstrum i filtru mogą być różne

Zaleta współczynników cepstrum: mała korelacja wzajemna.

W modelach HMM: macierz kowariancji w postaci diagonalnej.

Techniki homomorficzne

Podstawowe techniki liniowe

Zakłócenia i interferencje mogą łączyć się z sygnałami użytecznymi w sposób addytywny, ale również multiplikatywny i splotowy.

Techniki nieliniowe:

• redukcja szerokopasmowych zakłóceń w sygnale mowy,

• zmienny w czasie filtr Wienera,

• homomorficzne przetwarzanie sygnałów.

„Homomorficzne” oznacza „o tej samej strukturze”

Sygnały łączące się w sposób nieliniowy (tzn. inny niż liniowy) nie mogą być rozdzielane za pomocą filtracji liniowej. Techniki homomorficzne usiłują rozdzielać sygnały połączone w sposób nieliniowy w taki sposób, aby problem stał się liniowy (jest przekształcany do takiej samej struktury jak system liniowy).

Iloczyn sygnałów

przekształcenie homomorficzne - logarytm - zamienia mnożenie na dodawanie

Log^-1 jest funkcją e^x

Przykład

Automatyczna regulacja wzmocnienia sygnału radiowego AM

a[ ] - sygnał głosowy (200 Hz - 3,2 kHz)

g[ ] - sygnał wzmocnienia (kilka Hz)

Widmo logarytmu sygnałów jest bardziej złożone, czyli dobór filtru liniowego (górnoprzepustowego) może nie być prosty

Splot sygnałów

Przekształcenie homomorficzne składa się z dwóch etapów - przekształcenia Fouriera F (zmienia splot w mnożenie) i logarytmu - zamienia mnożenie na dodawanie

Odwrotne przekształcenie homomorficzne składa się z dwóch etapów - przekształcenia Log^-1, czyli wyznaczenia funkcji e^x i odwrotnego przekształcenia Fouriera F^-1.

Przykład

Usunięcie echa z sygnału dźwiękowego

Oddzielenie tonu krtaniowego od odpowiedzi impulsowej traktu głosowego

Filtracji liniowej poddawane są funkcje (sygnały) w dziedzinie częstotliwości - gdy normalnie dotyczy ona sygnałów w dziedzinie czasu. Zatem dziedziny czasu i częstotliwości zamieniły się.

Jest to uproszczony opis złożonych algorytmów przetwarzania homomorficznego. Zarówno przekształcenia Fouriera jak i logarytmowanie musi być zespolone (sygnał wejściowy przyjmuje wartości dodatnie i ujemne).

Jest problem aliasingu. Digitalizacja sygnału sinusoidalnego wymaga dwóch lub więcej próbek na okres. Ale digitalizacja logarytmu sygnału sinusoidalnego wymaga dużo więcej próbek na okres, nawet 100 razy więcej. Dla sygnału dźwiękowego może to oznaczać konieczność zastosowania częstotliwości próbkowania nawet powyżej 100 kHz, gdy standardowo (bez logarytmowania) wystarcza 8 kHz.

Widmo logarytmu sygnałów jest bardziej złożone, czyli dobór filtru liniowego może nie być prosty (nie ma gwarancji, że sygnały uda się odseparować drogą filtracji liniowej)

Sygnały powinny być przetwarzane w sposób spójny ze sposobem ich tworzenia - najpierw trzeba zrozumieć jak reprezentowana jest informacja w przetwarzanym sygnale.

Przetwarzanie cepstralne

Technikę przetwarzania cepstralnego stosuje się do wydzielenia z sygnału mowy sygnału pobudzenia i charakterystyk traktu głosowego.

Umożliwia estymację częstotliwości pobudzenia oraz częstotliwości formantów.

Wyznaczanie cepstrum:

• Sygnał mowy
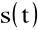
  jest splotem pobudzenia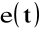
  i odpowiedzi impulsowej traktu wokalnego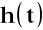
  :

• DFT sygnału mowy:

• Logarytm powyższej transformaty:

• odwrotne DFT

Wynik powyższych przekształceń w postaci widma logarytmu widma częstotliwościowego nazywany jest cepstrum (anagram spectrum). Oś odciętych wykresu cepstrum, posiadającą wymiar czasu, nazywana jest quefrency (anagram fequency) (Noll, 1964).

Cepstrum sygnału mowy zawiera duży szczyt odpowiadający tonowi podstawowemu, pozycja tego szczytu może być zastosowana do estymacji częstotliwości podstawowej.

Gdy ten szczyt zostanie usunięty przez wycięcie cepstrum poniżej tej quefrency, zniekształcenie widma spowodowane wpływem tonu podstawowego ulegnie redukcji. Przez wyznaczenie DFT dla cepstrum bez tonu podstawowego otrzymamy wygładzone widmo, w którym łatwiej identyfikuje się formanty.

Można rozdzielić sygnał pobudzenia (
) i charakterystykę traktu wokalnego (
).

stanowi składnik zajmujący zakres quefrency [0, 3,7] Ms. (3,7 ms to 1/270 Hz - najniższa częstotliwość formantowa dla mówcy-mężczyzny).Dynamika sygnałów

Założenie: statystyczna niezależność kolejnych wektorów obserwacji

W rzeczywistości: każda ramka sygnału mowy jest zależna od poprzedniej

Rozszerzenie wektora obserwacji o różnice parametrów statycznych

W szczególności są to współczynniki regresji I i II rzędu.

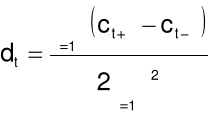
- współczynnik regresji pierwszego rzędu w
-tym momencie czasu,

do
- współczynniki statyczne,

- długość okna regresji.

Ta sama formuła zastosowana w stosunku do współczynników regresji pierwszego rzędu wyznacza wartości współczynników regresji drugiego rzędu.

Dla niektórych zastosowań:

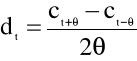
Współczynniki regresji pierwszego i drugiego rzędu są wyznaczane dla wszystkich parametrów statycznych łącznie z energią (czasem nawet znajomość wartości energii jest mniej przydatna niż jej regresja pierwszego i drugiego rzędu).

Perceptywna predykcja liniowa

(perceptual linear prediction, PLP)

Technika PLP jest odmianą oryginalnej analizy LPC i została wprowadzona przez Hermansky'ego w 1990 r.

Główna idea polegała na wykorzystaniu trzech podstawowych psychoakustycznych charakterystyk ludzkiego słuchu (charakterystyk słyszenia):

• nieliniowa rozdzielczość częstotliwościowa (pasma krytyczne),

• wrażliwość słuchu (krzywa równej głośności),

• prawo mocy „intensywność-głośność”.

Cechy analizy PLP:

1. bliższa percepcji człowieka niż tradycyjna technika LPC,

2. bardziej odporna na zmianę mówców niż LPC i MFCC,

3. obliczeniowo efektywna,

4. umożliwia oszczędną reprezentację mowy.

PLP wyznacza się w następujących krokach:

1. wydzielenie ramki (segmentu) z analizowanego sygnału mowy za pomocą okna Hamminga

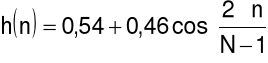
gdzie
jest długością okna

2. wyznaczenie widma mocy dla sygnału z ramki

gdzie
jest widmem (FFT)

3. zmiana w widmie mocy liniowej skali częstotliwości na skalę Bark za pomocą następującej aproksymacji

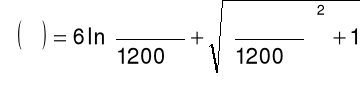
gdzie
jest pulsacją w [rad/s]

4. wyznaczenie splotu przeskalowanego widma z widmem mocy filtru pasm krytycznych, aproksymowanego zależnością:

dyskretny splot wyznacza się wg zależności:

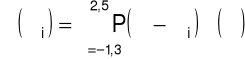
Kroki 3-4 są traktowane jak konstruowanie banku filtrów w skali Bark

5. w związku z potrzebą kompensacji nierównomiernej percepcji głośności przy różnych częstotliwościach wykonywana jest pre-emfaza:

czyli ważenie wyjścia filtrów w skali Bark za pomocą funkcji
reprezentującej aproksymację częstotliwościowej wrażliwości słuchowej człowieka (krzywa równej głośności):

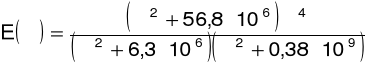
Dla aplikacji wymagających wysokich częstotliwości Nyquista należy dodać czynnik reprezentujący zmniejszoną wrażliwość ucha dla częstotliwości powyżej 5 kHz:

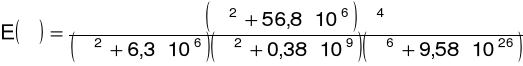
6. postrzegana głośność
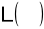
   jest w przybliżeniu pierwiastkiem sześciennym intensywności
   (zgodnie z prawem mocy Stevensa)

operacja jest wykorzystywana do redukcji widma amplitudowego pasm krytycznych (jest to rozsądna aproksymacja dla mowy, chociaż nie jest to prawdziwa dla bardzo głośnych i bardzo cichych dźwięków)

7. zastosować odwrotne przekształcenie Fouriera IDFT

8. wyznaczamy model predykcji liniowej (współczynniki predykcji)

9. opcjonalnie przekształcamy współczynniki predykcji we współczynniki cepstralne

Analiza relatywna widma RASTA-PLP

Większość technik estymacji parametrów mowy jest podatna na wpływy kanału transmisyjnego.

Analiza mowy techniką RASTA-PLP jest bardziej odporna na wpływy kanału transmisyjnego.

Słowo RASTA jest skrótem pojęcia RelAtive SpecTrAl.

Technika jest ulepszeniem metody PLP i polega na specjalnym filtrowaniu kanałów częstotliwościowych analizatora PLP.

RASTA zastępuje konwencjonalne widmo krótkookresowe w pasmach krytycznych bankiem filtrów, w którym jest tłumiona dowolna składowa stała lub wolnozmienna sygnału wejściowego.

Filtrowanie odbywa się dla widma logarytmicznego, stłumione stałe składowe widma odzwierciedlają wpływ czynników splotowych w wejściowym sygnale mowy, wprowadzonych przez charakterystyki częstotliwościowe mediów komunikacji.

Transmitancja filtru jest następująca:

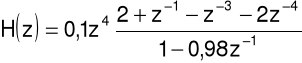
1

7

10

bank rozszerzających filtrów statycznych nieliniowych

bank liniowych filtrów pasmowych

bank filtrów kompresji statycznej nieliniowej

Rys. RASTA-PLP

współczynniki cepstralne RASTA-PLP

modelowanie autregresywne (IDFT, predykcja liniowa, cepstrum)

prawo mocy intensywność-głośność (kompresja nieliniowa ( )^0,33)

rozdzielczość widma wg pasm krytycznych (bank filtrów w skali Bark)

sygnał mowy

analiza widmowa (okno Hamminga, FFT, widmo mocy)

preemfaza dla wyrównania głośności (krzywa równej głośności)

Rys. Perceptywna predykcja liniowa (PLP)

współczynniki cepstralne PLP

modelowanie autoregresywne (IDFT, predykcja liniowa, opcjonalnie: cepstrum)

prawo mocy intensywność-głośność (kompresja nieliniowa ( )^0,33)

preemfaza dla wyrównania głośności (krzywa równej głośności)

rozdzielczość widma wg pasm krytycznych (bank filtrów w skali Bark)

sygnał mowy

analiza widmowa (okno Hamminga, FFT, widmo mocy)

---